
|
|
Основные источники и типы погрешностейЧИСЛЕННЫЕ МЕТОДЫ ОСНОВЫ ВЫЧИСЛИТЕЛЬНОЙ МАТЕМАТИКИ Вычислительная математика и её роль в современной науке и технике Под вычислительной математикой обычно понимают совокупность методов точного или приближенного численного решения различных математических задач. Здесь следует особо подчеркнуть значение численного решения, в котором основные результаты должны быть представлены в числовой форме. В традиционных разделах классического анализа часто достаточным оказывается получение формулы или уравнения, позволяющих в общем виде выразить изучаемые закономерности. Метод решения той или иной задачи точно так же может быть сформулирован в общей постановке. При этом в круг интересов исследователя обычно не входит вопрос о реализации этого метода в каждом конкретном случае. В технике и многих областях науки основным результатом решения задачи является ее численное решение. Независимо от того, производится ли определение напряжений и деформаций в элементах строительной конструкции или машины, скорости движения жидкости или газа в трубопроводе, расхода горючего при движении автомобиля по дороге, температуры в различных точках массива и т. п., специалиста, как правило, интересует решение задачи в числах. Современная вычислительная математика состоит из многих разделов, важнейшими из которых являются: - вычисление и интерполирование функций, - вычислительные методы линейной алгебры, - численные методы решения алгебраических и трансцендентных уравнений, - численное дифференцирование и интегрирование, - численное решение дифференциальных уравнений, - методы оптимизации, в которых изучаются численные приемы отыскания экстремальных значений функционалов. Создание и совершенствование быстродействующей вычислительной техники сделало возможным решение многих актуальных и сложных прикладных задач, способствовало тому, что численные методы превратились в область знаний, жизненно необходимую для функционирования практически всех областей народного хозяйства. При применении численных методов решения задач оказываются, как правило, приближенными. Объясняется это во многих случаях тем, что методы точного решения таких задач до настоящего времени неизвестны. Кроме того, даже при применении точного метода довольствуются приближенным решением, в частности, по следующим причинам: - получение точного решения оказывается очень трудоемким, в то же время приближенное решение при существенно меньшем объекте вычислений оказывается вполне приемлемым по своему характеру; - точность полученного результата не играет существенной роли, так как в любом случае округляется до целого числа (например, при определении количества механизмов, необходимого для выполнения данного объема работ); - приходится удовлетворяться приближенным решением, поскольку точное решение не может быть получено из-за неизбежных погрешностей возникающих в процессе вычислений. Следует отметить, что теория погрешностей является одним из основных разделов вычислительной математики. Элементы теории погрешностей Основные источники и типы погрешностей При решении прикладных задач очень важно иметь представление о точности полученных результатов. Погрешности, которые могут быть заключены в таких результатах, порождаются целым рядом причин; некоторые из них встречаются весьма часто. Это неустранимые погрешности, устранимые (погрешности численного метода) и погрешности округления. Рассмотрим каждую из них подробнее. 1. При решении многих задач в качестве исходных принимаются значения величин, полученные из эксперимента. В силу целого ряда причин, в том числе ограниченной точности измерительной аппаратуры и влияния различных случайных факторов, экспериментальные данные всегда имеют погрешности того или иного порядка. Погрешности могут заключаться и в исходных данных, полученных теоретически. Естественно, что эти погрешности оказывают в той или иной мере влияние на результаты решения задачи, однако никакими мерами в ходе решения такие погрешности устранить нельзя. Поэтому погрешности такого типа часто называют неустранимыми. 2. В случае, когда решить задачу точно не представляется возможным, приходится применять различные приближенные методы. Результаты решения заведомо содержат погрешности, характер которых зависит от используемого приближенного метода. В этом случае мы имеем погрешности метода, которые являются устранимыми. 3. С погрешностями округления особенно приходится считаться при реализации неустойчивых вычислительных процессов, в которых незначительные погрешности в исходных данных или результатах промежуточных вычислений могут привести к существенным ошибкам в конечном результате. Точные значения многих величин практически никогда не могут быть введены в процесс вычислений, например, иррациональных величин Виды погрешностей Мерой точности приближенного числа является погрешность. Пусть Под абсолютной погрешностью
Часто знак погрешности неизвестен или не имеет значения. Тогда в рассмотрение вводится абсолютная погрешность приближенного числа
Относительной погрешностью
Как видно из формул, абсолютная погрешность имеет размерность оцениваемых этой погрешностью величин, относительная погрешность всегда безразмерна. Величины В качестве предельной абсолютной погрешности
Аналогично в качестве предельной относительной погрешности
При анализе серии измерений в качестве значений 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
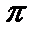 ,
, 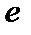 ,
, 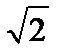 и др. В этих случаях также неизбежны погрешности округления.
и др. В этих случаях также неизбежны погрешности округления. - точное значение числа,
- точное значение числа, 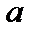 - его приближенное значение.
- его приближенное значение. понимается разность между соответствующим точным значениями рассматриваемой величины
понимается разность между соответствующим точным значениями рассматриваемой величины  . Погрешность выражается так:
. Погрешность выражается так: . (2.1)
. (2.1) . (2.2)
. (2.2) приближенного значения величины, точное значение которой равно
приближенного значения величины, точное значение которой равно 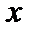 , называется отношение его абсолютной погрешности
, называется отношение его абсолютной погрешности  к модулю точного или приближенного значения, т. е.
к модулю точного или приближенного значения, т. е.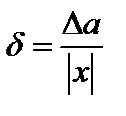 ; (2.3.)
; (2.3.)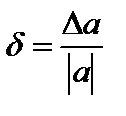 . (2.4)
. (2.4) и
и  приближенного числа может быть принято любое число, не меньшее абсолютной погрешности этого числа:
приближенного числа может быть принято любое число, не меньшее абсолютной погрешности этого числа: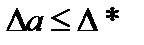 или
или  . (2.5)
. (2.5) приближенного числа может быть принято всякое число, удовлетворяющее условию
приближенного числа может быть принято всякое число, удовлетворяющее условию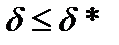 . (2.6)
. (2.6)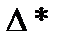 и
и 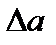 и
и