|
Метод бисекции (половинного деления)
Метод заключается в том, что отрезок  делиться пополам точкой делиться пополам точкой  и вычисляется значение функции и вычисляется значение функции  . Из двух полученных отрезков . Из двух полученных отрезков  и и  выбирается тот, на концах которого функция выбирается тот, на концах которого функция  имеет разные знаки и внутри которого, следовательно, лежит искомый корень. имеет разные знаки и внутри которого, следовательно, лежит искомый корень.
К недостаткам этого метода можно отнести то, что он требует обычно большого количества вычислений.
Пример 6.
Найти действительный корень уравнения  с точностью до ε = 0,01. с точностью до ε = 0,01.
Решение.
I этап: Выясним, имеет ли уравнение действительные корни, и если имеет, то сколько. Для этого нужно убедиться в следующем:
1)  непрерывна – она действительно непрерывна на непрерывна – она действительно непрерывна на 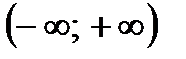 . .
2)  имеет на концах промежутка имеет на концах промежутка  значения разных знаков. значения разных знаков.
Представим  в виде: в виде:  , тогда , тогда 

3) чтобы определить, сколько действительных корней имеет уравнение, нужно выделить промежутки монотонности функции. Для этого найдем  и её корни: и её корни:
 . .
Они делят промежуток 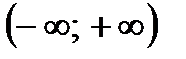 на три промежутка на три промежутка  , на каждом из которых может быть только один корень. , на каждом из которых может быть только один корень.
На    , т.е. на этом промежутке корней нет. , т.е. на этом промежутке корней нет.
На 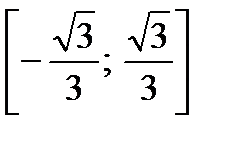   т.е. на этом промежутке корней нет. т.е. на этом промежутке корней нет.
На    , т.е. на этом промежутке имеется один действительный корень. , т.е. на этом промежутке имеется один действительный корень.
II этап: Требуется отделить этот корень. Вычисляя значения функции  в точках в точках  , выделим отрезок длиной в единицу, на котором находится корень: , выделим отрезок длиной в единицу, на котором находится корень:



Значит, корень лежит на отрезке  . .
III этап. Уточним корень методом бисекции (половинного деления).
Найдем  . Т.к. . Т.к.  проводим вычисления дальше. проводим вычисления дальше.
  , следовательно, необходимо рассмотреть отрезок , следовательно, необходимо рассмотреть отрезок 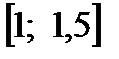 . Найдем . Найдем  . Т.к. . Т.к.  проводим вычисления дальше. проводим вычисления дальше.
 , ,  , следовательно, необходимо рассмотреть отрезок , следовательно, необходимо рассмотреть отрезок  . Найдем . Найдем  . Т.к. . Т.к.  проводим вычисления дальше. проводим вычисления дальше.
 , ,  , следовательно, необходимо рассмотреть отрезок , следовательно, необходимо рассмотреть отрезок  . Найдем . Найдем  . Т.к. . Т.к.  проводим вычисления дальше. проводим вычисления дальше.
 , , 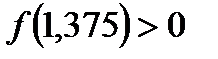 , следовательно, необходимо рассмотреть отрезок , следовательно, необходимо рассмотреть отрезок  . Найдем . Найдем  . Т.к. . Т.к.  проводим вычисления дальше. проводим вычисления дальше.
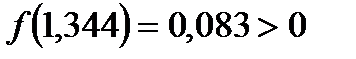 , ,  , следовательно, необходимо рассмотреть отрезок , следовательно, необходимо рассмотреть отрезок  . Найдем . Найдем  . Т.к. . Т.к.  проводим вычисления дальше. проводим вычисления дальше.
 , ,  , следовательно, необходимо рассмотреть отрезок , следовательно, необходимо рассмотреть отрезок  . Найдем . Найдем  . Т.к. . Т.к.  проводим вычисления дальше. проводим вычисления дальше.
 , ,  , следовательно, необходимо рассмотреть отрезок , следовательно, необходимо рассмотреть отрезок  . Найдем . Найдем  . Т.к. . Т.к.  , следовательно, корень уравнения равен , следовательно, корень уравнения равен 
Ответ: 
Метод хорд
Метод хорд состоит в том, что в качестве приближенного значения корня выбирают точку  пересечения с осью Ох хорды, соединяющей концы дуги графика функции пересечения с осью Ох хорды, соединяющей концы дуги графика функции  на отрезке на отрезке  (рис. 4). (рис. 4).

Рис. 4.
Получим формулу для вычисления с, если известны  . .
Уравнение хорды АВ запишем в виде:
 , ,
откуда получаем для точки её пересечения с осью Ох (точка  ): ):

или
 . (4.3) . (4.3)
Из двух полученных отрезков  и и  выбирается тот, на концах которого функция выбирается тот, на концах которого функция  имеет разные знаки. имеет разные знаки.
Применяя метод хорд, мы приближаемся к корню только с одной стороны, один из концов отрезка  остается неподвижным. остается неподвижным.
Если  , то неподвижным остается левый конец, а формула (4.3) принимает следующий вид: , то неподвижным остается левый конец, а формула (4.3) принимает следующий вид:
 . (4.4) . (4.4)
Если  , то неподвижным остается правый конец, а формула для вычисления выглядит следующим образом: , то неподвижным остается правый конец, а формула для вычисления выглядит следующим образом:
 . (4.5) . (4.5)
Пример 7.
Условие задачи сформулировано в примере 6.
Решение.
I и II этапы: разобраны в примере 6.
III этап. Уточним корень методом хорд.
Найдем вторую производную функции  : :  , ,  . На отрезке . На отрезке  , а , а  , следовательно, неподвижным останется правый конец. И в этом случае применим формулу (4.5): , следовательно, неподвижным останется правый конец. И в этом случае применим формулу (4.5):
 , ,
где  , ,  . .
Таблица 4.1

| 
| 
| |
| 1,000
| -1,000
| |
| 1,167
| -0,579
| |
| 1,253
| -0,285
| |
| 1,293
| -0,130
| |
| 1,311
| -0,057
| |
| 1,319
| -0,024
| |
| 1,322
| -0,010
| |
| 1,324
| -0,004
| |
| 1,324
| -0,002
| |
| 1,325
| -0,001
| |
| 1,325
| 0,000
| Ответ: 
Метод касательных (Ньютона)
Метод касательных состоит в том, что в качестве приближенного значения корня выбирают  – точку пересечения с осью Ох касательной, проведенной к одному из концов графика функции – точку пересечения с осью Ох касательной, проведенной к одному из концов графика функции  на отрезке на отрезке  (рис. 5). (рис. 5).
Чтобы точка с находилась на отрезке  , касательную следует провести через тот конец графика функции, в котором совпадает знак самой функции и её второй производной, т.е. , касательную следует провести через тот конец графика функции, в котором совпадает знак самой функции и её второй производной, т.е.  . .
Например, при изображении кривой на рис. 5 касательную следует проводить в точке В, т.к. в ней  и и  , а следовательно , а следовательно  . Если же провести касательную в точке А, то точка её пересечения с осью Ох окажется за пределами отрезка . Если же провести касательную в точке А, то точка её пересечения с осью Ох окажется за пределами отрезка  . .

Рис. 5.
Уравнение касательной к кривой  в точке В: в точке В:
 . .
Полагая  , находим , находим
 . (4.6) . (4.6)
Из двух полученных отрезков  и и  выбирается тот, на концах которого функция выбирается тот, на концах которого функция  имеет разные знаки. имеет разные знаки.
Пример 8.
Условие задачи сформулировано в примере 6.
Решение.
I и II этапы: разобраны в примере 6.
III этап. Уточним корень методом касательных.
Из предыдущей задачи известно, что на отрезке  , а , а  , следовательно, за начальное приближение необходимо приять , следовательно, за начальное приближение необходимо приять  . В этом случае формула (4.6) примет вид: . В этом случае формула (4.6) примет вид:
 . .
Таблица 4.2

| 
| 
| 
| |
| 1,000
| -1,000
| 2,000
| |
| 1,500
| 0,875
| 5,750
| |
| 1,348
| 0,101
| 4,450
| |
| 1,325
| 0,002
| 4,268
| |
| 1,325
| 0,000
| 4,265
|
Ответ: 
Численное интегрирование
Вычисление интегралов встречается при моделировании достаточно часто. Численные методы обычно применяются при взятии неберущихся интегралов от достаточно сложных функций, которые предварительно табулируются, или интегрирования таблично заданных функций.
Не нашли, что искали? Воспользуйтесь поиском по сайту:
©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|


 делиться пополам точкой
делиться пополам точкой  и вычисляется значение функции
и вычисляется значение функции  . Из двух полученных отрезков
. Из двух полученных отрезков  и
и  выбирается тот, на концах которого функция
выбирается тот, на концах которого функция  имеет разные знаки и внутри которого, следовательно, лежит искомый корень.
имеет разные знаки и внутри которого, следовательно, лежит искомый корень. с точностью до ε = 0,01.
с точностью до ε = 0,01. непрерывна – она действительно непрерывна на
непрерывна – она действительно непрерывна на 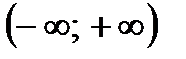 .
. имеет на концах промежутка
имеет на концах промежутка  значения разных знаков.
значения разных знаков. , тогда
, тогда 

 и её корни:
и её корни: .
. , на каждом из которых может быть только один корень.
, на каждом из которых может быть только один корень.

 , т.е. на этом промежутке корней нет.
, т.е. на этом промежутке корней нет.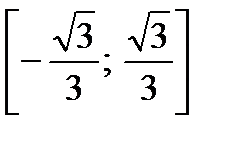

 т.е. на этом промежутке корней нет.
т.е. на этом промежутке корней нет.

 , т.е. на этом промежутке имеется один действительный корень.
, т.е. на этом промежутке имеется один действительный корень. , выделим отрезок длиной в единицу, на котором находится корень:
, выделим отрезок длиной в единицу, на котором находится корень:


 .
. . Т.к.
. Т.к.  проводим вычисления дальше.
проводим вычисления дальше.
 , следовательно, необходимо рассмотреть отрезок
, следовательно, необходимо рассмотреть отрезок 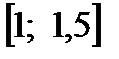 . Найдем
. Найдем  . Т.к.
. Т.к.  проводим вычисления дальше.
проводим вычисления дальше. ,
,  , следовательно, необходимо рассмотреть отрезок
, следовательно, необходимо рассмотреть отрезок  . Найдем
. Найдем  . Т.к.
. Т.к.  проводим вычисления дальше.
проводим вычисления дальше. ,
,  , следовательно, необходимо рассмотреть отрезок
, следовательно, необходимо рассмотреть отрезок  . Найдем
. Найдем  . Т.к.
. Т.к.  проводим вычисления дальше.
проводим вычисления дальше. ,
, 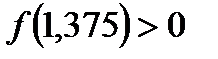 , следовательно, необходимо рассмотреть отрезок
, следовательно, необходимо рассмотреть отрезок  . Найдем
. Найдем  . Т.к.
. Т.к.  проводим вычисления дальше.
проводим вычисления дальше.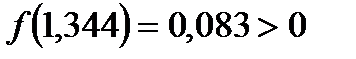 ,
,  , следовательно, необходимо рассмотреть отрезок
, следовательно, необходимо рассмотреть отрезок  . Найдем
. Найдем  . Т.к.
. Т.к.  проводим вычисления дальше.
проводим вычисления дальше. ,
,  , следовательно, необходимо рассмотреть отрезок
, следовательно, необходимо рассмотреть отрезок  . Найдем
. Найдем  . Т.к.
. Т.к.  проводим вычисления дальше.
проводим вычисления дальше. ,
,  , следовательно, необходимо рассмотреть отрезок
, следовательно, необходимо рассмотреть отрезок  . Найдем
. Найдем  . Т.к.
. Т.к.  , следовательно, корень уравнения равен
, следовательно, корень уравнения равен 

 пересечения с осью Ох хорды, соединяющей концы дуги графика функции
пересечения с осью Ох хорды, соединяющей концы дуги графика функции  на отрезке
на отрезке  .
. ,
, ):
):
 . (4.3)
. (4.3) и
и  , то неподвижным остается левый конец, а формула (4.3) принимает следующий вид:
, то неподвижным остается левый конец, а формула (4.3) принимает следующий вид: . (4.4)
. (4.4) , то неподвижным остается правый конец, а формула для вычисления выглядит следующим образом:
, то неподвижным остается правый конец, а формула для вычисления выглядит следующим образом: . (4.5)
. (4.5) :
:  ,
,  . На отрезке
. На отрезке  , а
, а  , следовательно, неподвижным останется правый конец. И в этом случае применим формулу (4.5):
, следовательно, неподвижным останется правый конец. И в этом случае применим формулу (4.5): ,
, ,
,  .
.



 – точку пересечения с осью Ох касательной, проведенной к одному из концов графика функции
– точку пересечения с осью Ох касательной, проведенной к одному из концов графика функции  на отрезке
на отрезке  .
. и
и  , а следовательно
, а следовательно  . Если же провести касательную в точке А, то точка её пересечения с осью Ох окажется за пределами отрезка
. Если же провести касательную в точке А, то точка её пересечения с осью Ох окажется за пределами отрезка  .
. . (4.6)
. (4.6) . В этом случае формула (4.6) примет вид:
. В этом случае формула (4.6) примет вид: .
.