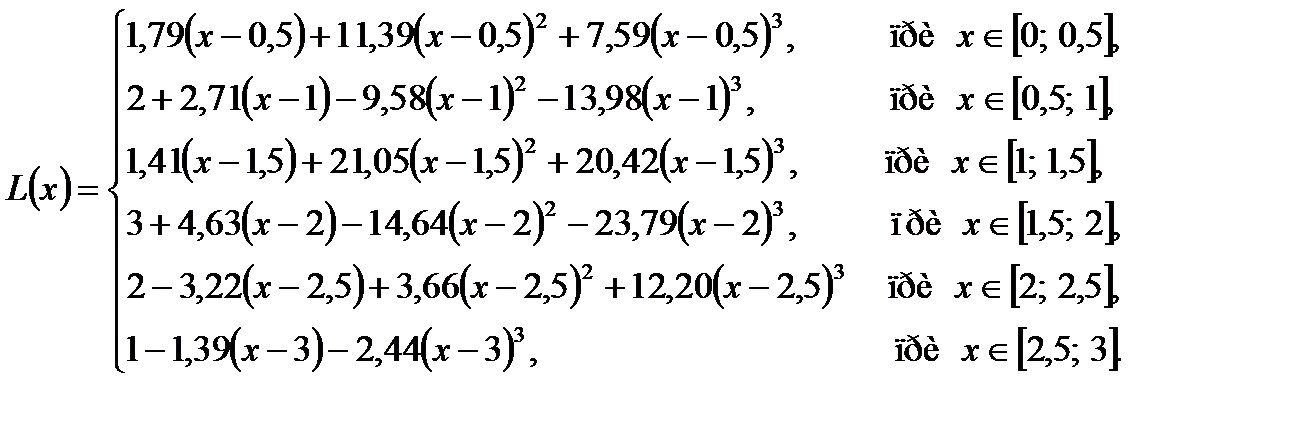|
|
Запись приближенных чиселЗначащей цифрой числа называется всякая входящая в его десятичное изображение цифра, отличная от нуля, и нуль, если он содержится между значащими цифрами или выражает десятичный разряд, который должен быть сохранен в изображении числа. По умолчанию принято записывать в числах только верные знаки, так, чтобы по записи числа в них можно было определить его погрешность. Цифра Цифра В процессе вычисления мы должны оставлять верные цифры, все остальные отбрасывать по правилу округления. Например, если задано число 5,198757, то в случае погрешности ±0,00000004 его следует записать в виде 5,1987570, а случае погрешности, равной ±0,000006, следует вначале округлить погрешность (получим 0,000006»0,00001), а затем правильно записать само число 5,1988. Округление чисел Применяют один из трех способов округления: по недостатку, по избытку и с поправкой. При округлении число разрядов определяется слева направо, начиная с разряда, содержащего первую слева значащую цифру. При округлении по недостатку положительного числа до При округлении по избытку до При округлении с поправкой до При округлении с поправкой до Например, при округлении с поправкой числа 25,1879 до четвертого разряда отбрасываем цифры 7 и 9 соответственно в пятом и шестом разрядах, а к оставшемуся числу 25,18 прибавляем единицу в четвертом разряде, т. е. число 0,01. Таким образом, округленное с поправкой до четвертого разряда число 25,1879 выражается числом 25,19. Таблица 2.1
При применении правила округления с поправкой абсолютная погрешность числа не превышает половины единицы десятичного разряда, выражаемого последней оставляемой значащей цифрой. Приведем теоремы, применяемые для оценки погрешностей результатов арифметических действий: Теорема 1. Абсолютная погрешность алгебраической суммы нескольких приближенных чисел не превышает суммы абсолютных погрешностей этих чисел. Теорема 2. При сложении приближенных величин одного и того же знака относительная погрешность суммы выражается величиной, заключенной между наибольшей и наименьшей относи тельными погрешностями слагаемых. Теорема 3. Предельная абсолютная погрешность разности равна сумме предельных погрешностей уменьшаемого и вычитаемого. Теорема 4. Относительная погрешность произведения нескольких приближенных чисел, отличных от нуля, не превышает суммы относительных погрешностей этих чисел. Теорема 5. Относительная погрешность частного не превышает суммы относительных погрешностей делимого и делителя. Пользуясь данными теоремами, рассмотрим несколько примеров. Пример 1. Найти сумму трех чисел Решение. Абсолютные погрешности чисел
Вычислим сумму максимально возможных значений абсолютных погрешностей:
В соответствии с теоремой 1 абсолютная погрешность
В качестве предельной абсолютной погрешности может быть принята величина Пусть известны относительные погрешности слагаемых
Пример 2. Найти предельную абсолютную погрешность числа Решение. Абсолютные погрешности чисел
В качестве предельных абсолютных погрешностей примем Тогда в соответствии с теоремой 3 предельная абсолютная погрешность числа
Пример 3. Оценить относительную погрешность Решение. Из теоремы 4 следует, что относительная погрешность произведения
На основании теоремы 5 искомая величина
ИНТЕРПОЛяция Основная задача интерполяции – нахождение значения таблично заданных функций в тех точках внутри данного интервала, где она не задана. Экстраполяция – восстановление функции за пределами заданного интервала. Концепция интерполяции Решение задач интерполяции и экстраполяции обеспечивается построением интерполяционной функции Пусть заданы значения функции Функция Различают следующие виды интерполирования функции 1. Локальное (или кусочное) интерполирование. В этом случае интерполирующая функция 2. Глобальное интерполирование – в случае, когда интерполирующая функция В связи с интерполяцией рассматривают три основные проблемы: 1) выбор интерполяционной функции 2) оценка погрешности интерполяции 3) размещение узлов интерполяции для обеспечения наивысшей возможной точности восстановления функции. Метод Лагранжа Пусть задана функция Для удобства этот многочлен будем искать в виде линейной комбинации многочленов:
где
При этом Подставив эти многочлены в формулу (3.1.), получим многочлен, называемый полиномом Лагранжа:
Погрешность полинома Лагранжа оценивается по формуле
где Пример 4. Составить интерполяционный многочлен Лагранжа для функции Таблица 3.1
Построить график полученного многочлена. Решение. В соответствии с заданной таблицей в качестве узлов интерполяции примем
График полученного полинома Лагранжа представлен на рисунке 1.

Рис. 1. График функции Метод сплайнов В ряде случаев возникает задача восстановления не только значений функции, но также её первой и второй производной. Это, конечно, можно сделать получив и продифференцировав интерполяционный полином. Но такой случай дает низкую точность восстановления производных. Для решения указанного класса задач применяется сплайновая интерполяция. Для достижения более высокой точности интерполирования функций и их производных применяют сплайны более высоких порядков. Наиболее широкое применение в настоящее время получил кубический сплайн. Сплайн – способ аппроксимации[1] функции, заданной таблично с помощью набора кусочно-полиномных зависимостей. Исторически понятие сплайна[2] связывают с гибкой линейкой, применяемой в чертежных работах. Из курса механики деформируемых стержней известно уравнение изгиба упругого стержня:
где
имеющее решение, представляемое кубическим полиномом:
Иными словами, гибкая линейка, помещенная на плоскости, плавно изогнется так, что её форму между любыми двумя соседними точками можно описать кубической параболой. Кубический сплайн Пусть на отрезке Потребуем, чтобы сплайн а) на каждом сегменте б) совпадает со значениями аппроксимирующей функции в узлах интерполирования; в) непрерывен вместе со своей первой г) выполняются краевые условия Сплайн
Для всего интервала будет соответственно п кубических полиномов, отличающихся коэффициентами Наглядная структура сплайна представлена на рисунке 2. Рис. 2. Расположение узлов и звеньев кубического сплайна. Коэффициенты определяются из следующих условий: - равенство значений сплайнов - условие гладкой стыковки звеньев сплайна (выполнение условия в)): - краевые условия (выполнение условия г)): Подставляя в условия выражения сплайна для краткости
Будем исключать из системы неизвестные Подставляя значения (3.6) в равенства (3.5) и (3.7), получим выражение
Из (3.9) и (3.10), учитывая
С помощью формулы (3.13) избавимся от
После подстановки данных формул в выражение (3.8) детализированной системы, получим выражение, в котором неизвестны только коэффициенты
(3.15) Получаем замкнутую систему, решаемую методом прогонки. Применение этого метода сводится к вычислению прогоночных коэффициентов по формулам прямой прогонки, затем получение искомых коэффициентов сплайна обратной прогонкой. Для сокращения записи представим формулу (3.15) в виде
где коэффициенты
при В процессе прямого хода прогонки вычисляем прогоночные коэффициенты:
На обратном ходе имеем
полагая в ней Для восстановления производных можно продифференцировать на каждом участке соответствующий кубический полином. В случае необходимости определения производных в узлах существуют специальные приемы, сводящие определение производных к решению более простой системы уравнений относительно искомых производных второго или первого порядка. К важным достоинствам интерполяции кубическими сплайнами относится получение функции, имеющей минимальную возможную кривизну. К недостаткам сплайновой интерполяции относится необходимость получения сравнительно большого числа параметров. Пример 5. Построить кубический интерполирующий сплайн для функции Таблица 3.2
Найдем значения Таблица 3.3
Вычислим прогоночные коэффициенты Таблица 3.4
На обратном ходе найдем коэффициенты Таблица 3.5
Найдем коэффициенты Таблица 3.6
Получаем кубический интерполирующий сплайн, график которого представлен на рисунке 3:

Рис.3. График кубического интерполирующего сплайна. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 называется верной в широком смысле, если абсолютная погрешность числа не превосходит единицы последнего разряда. Например, в случае 2,145±0,0008 все цифры верные.
называется верной в широком смысле, если абсолютная погрешность числа не превосходит единицы последнего разряда. Например, в случае 2,145±0,0008 все цифры верные. . Это выполнимо в случае 2,145±0,0004.
. Это выполнимо в случае 2,145±0,0004. -ого разряда сохраняют неизменными все цифры в разрядах слева направо вплоть до
-ого разряда сохраняют неизменными все цифры в разрядах слева направо вплоть до  -ого, отбрасывают, а из оставшегося числа вычитают единицу в
-ого, отбрасывают, а из оставшегося числа вычитают единицу в  -ого, отбрасывают, а к оставшемуся числу прибавляют единицу в
-ого, отбрасывают, а к оставшемуся числу прибавляют единицу в  -ого, цифры в первых
-ого, цифры в первых 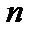 разрядах сохраняют неизменными.
разрядах сохраняют неизменными. -ом разряде больше или равна 5, если же эта цифра меньше 5, то цифры в разрядах от первого до
-ом разряде больше или равна 5, если же эта цифра меньше 5, то цифры в разрядах от первого до  первых разрядах сохраняют неизменными, если цифра в
первых разрядах сохраняют неизменными, если цифра в  -разрядного числа вычитают единицу в
-разрядного числа вычитают единицу в 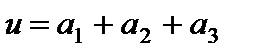 , где
, где  ,
,  ,
,  и оценить ее погрешность, если все приведенные в изображении этих чисел цифры являются верными
и оценить ее погрешность, если все приведенные в изображении этих чисел цифры являются верными ,
,  ,
,  удовлетворяют условиям
удовлетворяют условиям ;
;  ;
;  .
. .
. числа
числа  удовлетворяет условию:
удовлетворяет условию: .
. .
. ,
,  ,
,  . Тогда в соответствии с теоремой 2 относительная погрешность
. Тогда в соответствии с теоремой 2 относительная погрешность  суммы удовлетворяет условию
суммы удовлетворяет условию .
. , если в числах
, если в числах  ,
,  верными являются соответственно первые три и четыре цифры.
верными являются соответственно первые три и четыре цифры. и
и  удовлетворяют условиям
удовлетворяют условиям ;
;  .
. ;
;  .
. выражается суммой
выражается суммой .
. числа
числа  в случае, когда относительные погрешности приближенных чисел
в случае, когда относительные погрешности приближенных чисел  ,
,  ,
,  ,
,  соответственно равны
соответственно равны  ,
, 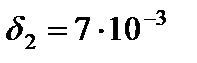 ,
,  ,
,  .
. не превышает суммы относительных погрешностей этих чисел, т.е.
не превышает суммы относительных погрешностей этих чисел, т.е.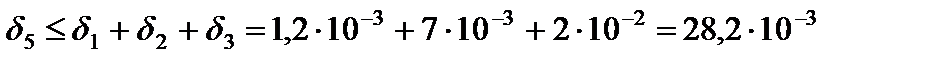
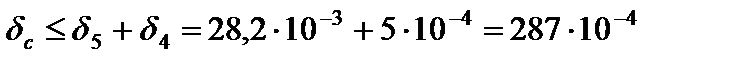
 , приближённо заменяющей исходную
, приближённо заменяющей исходную  , заданную таблично, и проходящей через все заданные точки – узлы интерполяции. С помощью этой функции можно рассчитать искомое значение исходной функции в любой точке.
, заданную таблично, и проходящей через все заданные точки – узлы интерполяции. С помощью этой функции можно рассчитать искомое значение исходной функции в любой точке. в точках
в точках  , где
, где  . Требуется подобрать такую функцию
. Требуется подобрать такую функцию 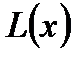 , чтобы значения этой функции в точках
, чтобы значения этой функции в точках  в этих точках:
в этих точках:  , а между этими точками отклонение было наименьшим.
, а между этими точками отклонение было наименьшим. называется интерполирующей по отношению к функции
называется интерполирующей по отношению к функции  :
: определена только на отрезке
определена только на отрезке  .
. .
. ;
; . Требуется подобрать многочлен
. Требуется подобрать многочлен  , порядка не выше
, порядка не выше  таким образом, чтобы его значения в точках
таким образом, чтобы его значения в точках  , а между ними отклонения были наименьшими.
, а между ними отклонения были наименьшими.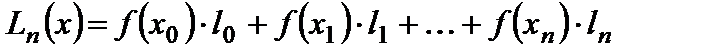 , (3.1)
, (3.1) - многочлены следующего вида:
- многочлены следующего вида: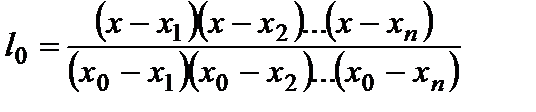
 и т.д.
и т.д. ,
,  и т.д., а в остальных точках эти многочлены равны нулю.
и т.д., а в остальных точках эти многочлены равны нулю. . (3.2.)
. (3.2.)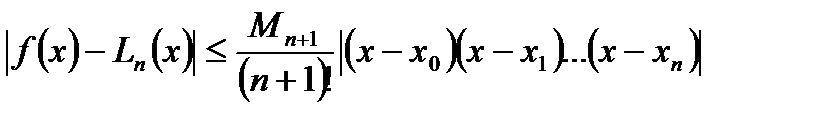 , (3.3)
, (3.3) – наибольшее значение
– наибольшее значение  -ой производной на отрезке
-ой производной на отрезке  .
.







 ,
,  ,
,  ,
,  и
и  . Составляем многочлен Лагранжа
. Составляем многочлен Лагранжа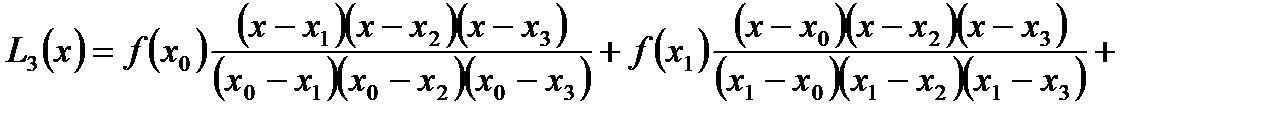
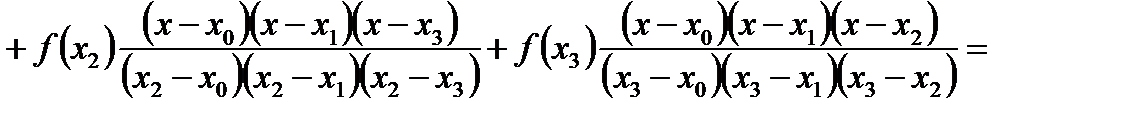
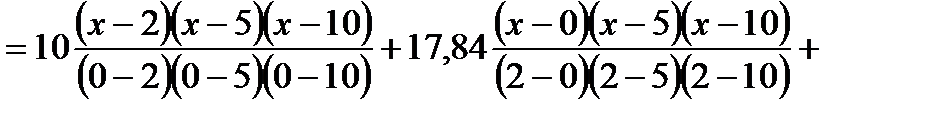
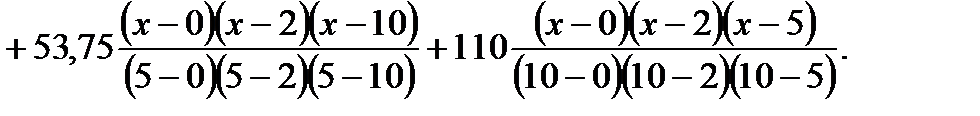
 .
. .
.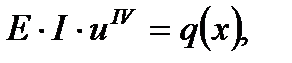
 – модуль упругости,
– модуль упругости,  – момент инерции поперечного сечения,
– момент инерции поперечного сечения,  – функция прогиба,
– функция прогиба,  – распределенная нагрузка. В случае отсутствия нагрузки получаем однородное уравнение
– распределенная нагрузка. В случае отсутствия нагрузки получаем однородное уравнение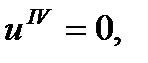
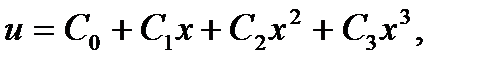
 – постоянные интегрирования, определяемые из граничных условий.
– постоянные интегрирования, определяемые из граничных условий. – узлах интерполирования.
– узлах интерполирования. удовлетворял следующим условия:
удовлетворял следующим условия: является полиномом третьей степени;
является полиномом третьей степени; и второй
и второй  производными;
производными; .
. отрезка
отрезка  . (3.4)
. (3.4) ,
,  ,
,  ,
,  , где
, где  - номер сплайна.
- номер сплайна. и аппроксимируемой функции
и аппроксимируемой функции  в узлах (выполнение условия б):
в узлах (выполнение условия б):  ;
; ;
; и его производных
и его производных  и
и  , и, полагая
, и, полагая , получаем детализированную систему связей:
, получаем детализированную систему связей: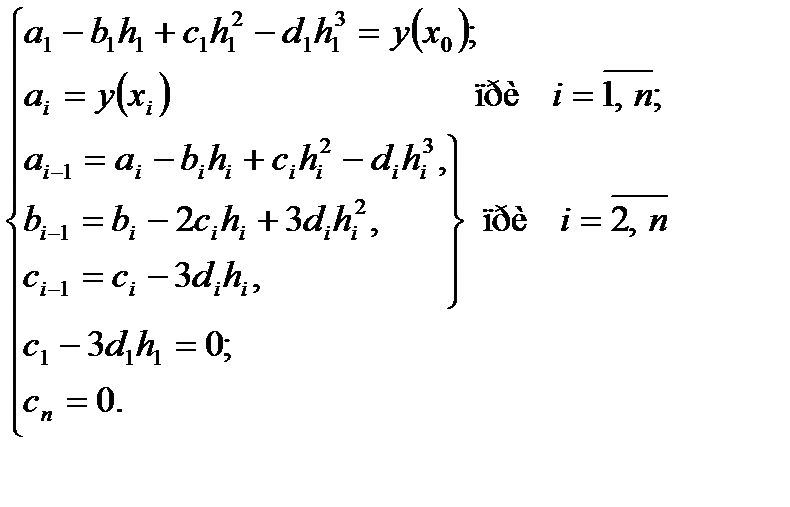
 .
. , при
, при  (3.12)
(3.12) :
: при
при 
 (3.14)
(3.14) :
: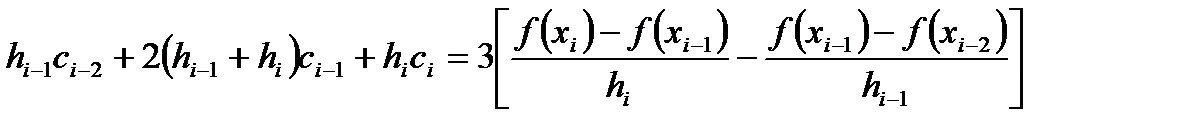
 ,
,  .
. , (3.16)
, (3.16) и
и  вычисляем по формулам:
вычисляем по формулам: (3.17)
(3.17) (3.18)
(3.18) , (3.19)
, (3.19) (3.20)
(3.20)
 (3.21)
(3.21)
 , (3.23)
, (3.23) и учитывая
и учитывая  . Затем по формуле (3.14) вычисляем коэффициенты
. Затем по формуле (3.14) вычисляем коэффициенты  .
.

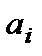 ,
,  ,
,  и
и  .
.
 и
и  методом прямой прогонки.
методом прямой прогонки. , используя формулу (3.23), полагая в ней
, используя формулу (3.23), полагая в ней  и учитывая
и учитывая  .
. :
: