
|
|
Магнитные свойства тела и веществаКривые намагничивания тела и вещества.Обычно требуется знать магнитные свойства ферромагнетиков как функции истинного, внутреннего магнитного поля. Однако на практике в большинстве случаев измеряется зависимость намагниченности от внешнего магнитного поля. Графический метод пересчета называется методом Релея (или методом сдвига).
Рис. 1.40. Построение кривой намагничивания материала (1) по кривой намагничивания тела (2)
На рис. 1.40 кривая 2 соответствует кривой намагничивания тела. Для того чтобы построить кривую намагничивания вещества
Если провести прямую параллельно оси поля ( внешнему полю Таким способом можно определить для каждой точки кривой Такое же перестроение можно произвести для петли гистерезиса. При этом легко убедиться, что коэрцитивная сила Можно также провести обратное построение и найти по кривой намагничивания материала кривую намагничивания тела с известным коэффициентом размагничивания, что используется при расчете различных магнитных устройств. Магнитные свойства тела и вещества.Для истинной напряженности магнитного поля мы можем написать выражения:
где Те же зависимости мы можем записать и для напряженности внешнего магнитного поля:
где Для одних и тех же значений намагниченности и индукции из выражений (1.116) и (1.118), а также выражений (1.117) и (1.119) следуют равенства
Напряженности истинного и внешнего магнитных полей связаны выражениями:
или Подставив выражение для
Аналогично, выразив из (1.122) и (1.123)
Из выражения (1.125) видно, что при
где Магнитные цепи Совокупность магнетиков, по которым проходит поток магнитной индукции, называют магнитной цепью. В магнитной дефектоскопии магнитной цепью может являться собственно изделие (например, коленчатый вал, намагничиваемый соленоидом) либо изделие совместно с приставным электромагнитом. Обычной является задача определения величины ампер-витков для получения заданного значения индукции в данном сечении изделия по заданному току. Для расчёта магнитных цепей используют закон полного тока
а также законы, аналогичные законам Ома и Кирхгофа для электрической цепи:
В приведенных выше выражениях использованы следующие обозначения:
причем
Рис. 1.41. К расчёту магнитной цепи с тороидом
Примеры расчетов магнитных цепей.1. Цепь, содержащая замкнутый ферромагнитный сердечник постоянного сечения. Необходимо в сердечнике получить заданную индукцию 2. Цепь, содержащая ферромагнитный сердечник переменного сечения (рис. 1.41б). Пренебрежём потоками рассеяния, то есть,

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|

 , необходимо знать размагничивающий фактор
, необходимо знать размагничивающий фактор  . Зная
. Зная 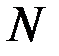 , можно построить зависимость намагниченности от размагничивающего поля
, можно построить зависимость намагниченности от размагничивающего поля  , используя соотношения (1.107) и (1.108). Из них видно, что это прямая линия, наклон которой к оси
, используя соотношения (1.107) и (1.108). Из них видно, что это прямая линия, наклон которой к оси  определяется равенством
определяется равенством . (1.115)
. (1.115) ,
,  ), то она пересечется с кривой
), то она пересечется с кривой  в точке
в точке  , соответствующей намагниченности
, соответствующей намагниченности  и
и , а с прямой
, а с прямой  в точке
в точке  . Величина отрезка
. Величина отрезка  соответствует величине размагничивающего поля при намагниченности
соответствует величине размагничивающего поля при намагниченности  . Чтобы получить значение истинного поля при
. Чтобы получить значение истинного поля при  , отложим на прямой, параллельной оси
, отложим на прямой, параллельной оси  , отрезок
, отрезок  . Тогда величина отрезка
. Тогда величина отрезка  дает значение внутреннего поля, соответствующее внешнему полю
дает значение внутреннего поля, соответствующее внешнему полю  .
. значение внутреннего поля и построить кривую намагниченности вещества (кривая 1 на рис. 1.40).
значение внутреннего поля и построить кривую намагниченности вещества (кривая 1 на рис. 1.40). остаётся неизменной для вещества и тела, а остаточная магнитная индукция
остаётся неизменной для вещества и тела, а остаточная магнитная индукция  для тела меньше, чем для вещества.
для тела меньше, чем для вещества. (1.116)
(1.116) , (1.117)
, (1.117) и
и  - восприимчивость и проницаемость материала (вещества).
- восприимчивость и проницаемость материала (вещества). (1.118)
(1.118) , (1.119)
, (1.119) и
и  , соответственно, восприимчивость и проницаемость тела.
, соответственно, восприимчивость и проницаемость тела. (1.120)
(1.120) . (1.121)
. (1.121) (1.122)
(1.122)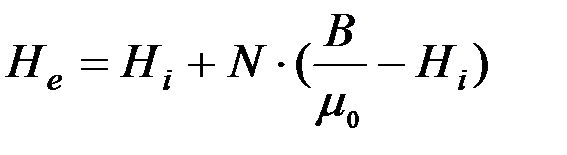 . (1.123)
. (1.123) из (1.122) в (1.120), а выражение (1.123) в (1.121), получим связь между восприимчивостями и проницаемостями тела и вещества:
из (1.122) в (1.120), а выражение (1.123) в (1.121), получим связь между восприимчивостями и проницаемостями тела и вещества: , (1.124)
, (1.124) . (1.125)
. (1.125) и подставив его в (1.120) и (1.121), получим:
и подставив его в (1.120) и (1.121), получим: , (1.126)
, (1.126) . (1.127)
. (1.127) проницаемость тела стремится к величине
проницаемость тела стремится к величине , (1.128)
, (1.128) - проницаемость формы, названная так потому, что зависит в основном от геометрических размеров. Аналогичный результат получается для восприимчивости. Значения
- проницаемость формы, названная так потому, что зависит в основном от геометрических размеров. Аналогичный результат получается для восприимчивости. Значения  и
и  могут быть измерены или рассчитаны.
могут быть измерены или рассчитаны. 
 , (1.129)
, (1.129) (для участка цепи) , (1.130)
(для участка цепи) , (1.130) (для узла цепи) , (1.131)
(для узла цепи) , (1.131) . (1.132)
. (1.132) - длина i-го участка магнитной цепи;
- длина i-го участка магнитной цепи;  - число витков намагничивающей катушки;
- число витков намагничивающей катушки; 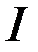 - намагничивающий ток;
- намагничивающий ток;  - намагничивающая сила;
- намагничивающая сила;  - разность магнитных потенциалов между концами участка цепи;
- разность магнитных потенциалов между концами участка цепи;  - магнитное сопротивление. При этом
- магнитное сопротивление. При этом ,
,  и
и  , (1.133)
, (1.133) – площадь поперечного сечения магнитопровода.
– площадь поперечного сечения магнитопровода.
 . По закону полного тока
. По закону полного тока  . Как видно из рис. 1.41а в этом случае
. Как видно из рис. 1.41а в этом случае  (считаем, что внутренний и внешний диаметры отличаются мало). Поле
(считаем, что внутренний и внешний диаметры отличаются мало). Поле  определяется по кривой
определяется по кривой  (рис. 1.41в). Пусть
(рис. 1.41в). Пусть  = 1,5 Тл,
= 1,5 Тл,  = 0,01 м. Находим
= 0,01 м. Находим  = 2000 А/м. Тогда
= 2000 А/м. Тогда 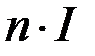 = 125,6 А.
= 125,6 А. , следовательно,
, следовательно, 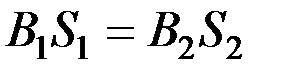 . Закон полного тока
. Закон полного тока 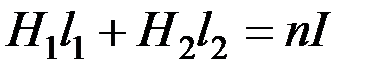 . Пусть необходимо в сечении
. Пусть необходимо в сечении  получить индукцию
получить индукцию  = 1,5 Тл, что, как показано выше, соответствует полю
= 1,5 Тл, что, как показано выше, соответствует полю 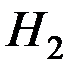 = 2000 А/м. Средний радиус сердечника
= 2000 А/м. Средний радиус сердечника  = 0,01 м. Пусть также
= 0,01 м. Пусть также  = 0,005 м, а
= 0,005 м, а  . Тогда индукция в сечении
. Тогда индукция в сечении  будет равна
будет равна 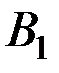 = 0,5.
= 0,5.  = 0,75 Тл. По рис. 1.41в находим
= 0,75 Тл. По рис. 1.41в находим  = 1200 А/м. Тогда,
= 1200 А/м. Тогда,  = 2000.
= 2000. 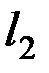 + 1200.
+ 1200.  = (2000.0,005 + 1200.0,0623) = 84,8 А. Эта величина существенно меньше, чем в предыдущем примере, т.е. для намагничивания участка меньшего сечения требуется меньшая величина ампер-витков (имеет место концентрация магнитного потока).
= (2000.0,005 + 1200.0,0623) = 84,8 А. Эта величина существенно меньше, чем в предыдущем примере, т.е. для намагничивания участка меньшего сечения требуется меньшая величина ампер-витков (имеет место концентрация магнитного потока).