|
Рекордсмены магнитных материалов
| Предельные свойства
| Материал
| |
мах индукция насыщения,×10-4 Тл
|
|
Пермендюр
50 Co + 50 Fe
| | мах проницаемость,
мах начальная проницаемость,
min коэрцитивная сила, А/м
| 1 000 000
100 000
0.16
|
Супермаллой
5 Mo, 79Ni, 16 Fe
| | мах коэрцитивная сила, кА/м
значение (ВН)мах/2, кДж/м3
|
| SmCo5
33,7 Sm 66,3 Co
| | мах значение
магнитострикции
| 10-3
-35×10-6
| Сплавы на основе РЗМ
ТbxDy1-xFe2
Чистые металлы Ni
|
Изменения состава, структуры и дефектности материалов приводят к очень большим вариациям магнитных свойств. В табл. 1.3. приведены рекордные к настоящему времени значения магнитных свойств материалов.
Намагничивание магнетиков конечных размеров
Коэффициент размагничивания. Ранее уже упоминались понятия размагничивающего поля и коэффициента размагничивания. Ввиду важности вопроса рассмотрим его подробнее.
 На границе магнетика конечных размеров меняется намагниченность, например на границе с воздухом намагниченность меняется от значения На границе магнетика конечных размеров меняется намагниченность, например на границе с воздухом намагниченность меняется от значения  (в ферромагнетике) до нуля (в воздухе). Если вектор намагниченности (в ферромагнетике) до нуля (в воздухе). Если вектор намагниченности  параллелен границе, то магнитный поток (как указывалось, магнитный поток через площадку параллелен границе, то магнитный поток (как указывалось, магнитный поток через площадку  пропорционален произведению нормальной к поверхности площадки составляющей магнитной индукции на площадь площадки пропорционален произведению нормальной к поверхности площадки составляющей магнитной индукции на площадь площадки  ) не выходит за пределы магнетика. Если намагниченность перпендикулярна границе, то на границе будут иметься полюса (величиной ) не выходит за пределы магнетика. Если намагниченность перпендикулярна границе, то на границе будут иметься полюса (величиной  , где , где  - площадь границы), являющиеся источником поля в воздухе. Но если есть полюс, то поле от него направлено во все стороны, в том числе и внутрь магнетика, так что внутри магнетика - площадь границы), являющиеся источником поля в воздухе. Но если есть полюс, то поле от него направлено во все стороны, в том числе и внутрь магнетика, так что внутри магнетика
 , (1.107) , (1.107)
где  - поле внутри магнетика; - поле внутри магнетика;  - внешнее поле (поле, создаваемое источником, например, соленоидом); - внешнее поле (поле, создаваемое источником, например, соленоидом);  - поле, обусловленное полюсами на границах образца (размагничивающее поле). - поле, обусловленное полюсами на границах образца (размагничивающее поле).
Очевидно, что величина полюсов на нормальных к намагниченности границах магнетика будет тем больше, чем больше намагниченность и, следовательно:
 , (1.108) , (1.108)
где  - коэффициент размагничивания (иногда называемый размагничивающим фактором), зависящий при однородном намагничивании только от формы магнетика. Однородно намагничиваются только эллипсоиды, для которых величина - коэффициент размагничивания (иногда называемый размагничивающим фактором), зависящий при однородном намагничивании только от формы магнетика. Однородно намагничиваются только эллипсоиды, для которых величина  может быть точно определена. В большинстве же случаев тело намагничивается неоднородно, может быть точно определена. В большинстве же случаев тело намагничивается неоднородно,  и и  будут в разных точках различны, поэтому пользуются некоторыми усреднёнными значениями будут в разных точках различны, поэтому пользуются некоторыми усреднёнными значениями  . Для проволоки диаметром . Для проволоки диаметром  , длиной , длиной  , намагничиваемой в направлении , намагничиваемой в направлении  , значения , значения  приведены в табл. 1.4. приведены в табл. 1.4.
Таблица 1.4
 / / 
|
|
|
|
|
|
|
|
| 
|
| 0,27
| 0,14
| 0,04
| 0,017
| 0,006
| 0,0013
| 13.10-6
|
Детальные расчёты размагничивающих коэффициентов однородных тел, ограниченных поверхностями второго порядка, то есть эллипсоидов, провёл И. Осборн. Формулы для коэффициентов  , ,  , ,  (соответствующих намагничиванию эллипсоида вдоль осей (соответствующих намагничиванию эллипсоида вдоль осей  , ,  , ,  )имеют достаточно сложный характер, но всегда выполняется )имеют достаточно сложный характер, но всегда выполняется
 . (1.109) . (1.109)
Таким образом, для некоторых случаев величину  можно определить очень просто. Очевидно, что для шара можно определить очень просто. Очевидно, что для шара  . Для бесконечно длинного цилиндра круглого сечения при его поперечном намагничивании . Для бесконечно длинного цилиндра круглого сечения при его поперечном намагничивании  . .
Условимся, что  . Пусть теперь . Пусть теперь  и и  (т.е. очень тонкий вытянутый сфероид, почти проволока), тогда коэффициенты размагничивания можно рассчитать по формулам: (т.е. очень тонкий вытянутый сфероид, почти проволока), тогда коэффициенты размагничивания можно рассчитать по формулам:
 , (1.110) , (1.110)
 . (1.111) . (1.111)
Значения  рассчитанные по (1.110) и приведённые в табл. 1.4 совпадают, начиная примерно с рассчитанные по (1.110) и приведённые в табл. 1.4 совпадают, начиная примерно с  (в соответствии с условием (в соответствии с условием  ). ).
Для эллиптического цилиндра  , ,  , следовательно , следовательно
 ; (1.112) ; (1.112)
для другой оси
 . (1.113) . (1.113)
Для этого случая так же, как и в (1.111), если  , то , то  (очень длинная проволока, намагничиваемая поперёк). (очень длинная проволока, намагничиваемая поперёк).
Приведём пример простого расчёта коэффициента  . Рассмотрим (рис. 1.39) прямоугольный параллелепипед (полосу), намагничиваемый полем . Рассмотрим (рис. 1.39) прямоугольный параллелепипед (полосу), намагничиваемый полем  перпендикулярно грани сечения наибольшего размера. Если величина заряда на единицу длины грани есть перпендикулярно грани сечения наибольшего размера. Если величина заряда на единицу длины грани есть 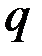 , то напряжённость поля, создаваемого одной гранью на расстоянии , то напряжённость поля, создаваемого одной гранью на расстоянии  ( (  , где , где 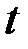 - толщина полосы), - толщина полосы),
 . .
 Поскольку плотность поверхностных зарядов Поскольку плотность поверхностных зарядов  , то , то  . .
Рис. 1.39. Пластина в поперечном магнитном поле
Для центрального сечения полосы шириной  расстояние от края расстояние от края 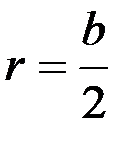 , а , а
полное поле создаётся двумя гранями и равно:
 . .
Поскольку  , то , то
 . (1.114) . (1.114)
Таким образом, коэффициент размагничивания определен.
Не нашли, что искали? Воспользуйтесь поиском по сайту:
©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|


 На границе магнетика конечных размеров меняется намагниченность, например на границе с воздухом намагниченность меняется от значения
На границе магнетика конечных размеров меняется намагниченность, например на границе с воздухом намагниченность меняется от значения  (в ферромагнетике) до нуля (в воздухе). Если вектор намагниченности
(в ферромагнетике) до нуля (в воздухе). Если вектор намагниченности  параллелен границе, то магнитный поток (как указывалось, магнитный поток через площадку
параллелен границе, то магнитный поток (как указывалось, магнитный поток через площадку  пропорционален произведению нормальной к поверхности площадки составляющей магнитной индукции на площадь площадки
пропорционален произведению нормальной к поверхности площадки составляющей магнитной индукции на площадь площадки  ) не выходит за пределы магнетика. Если намагниченность перпендикулярна границе, то на границе будут иметься полюса (величиной
) не выходит за пределы магнетика. Если намагниченность перпендикулярна границе, то на границе будут иметься полюса (величиной  , где
, где  - площадь границы), являющиеся источником поля в воздухе. Но если есть полюс, то поле от него направлено во все стороны, в том числе и внутрь магнетика, так что внутри магнетика
- площадь границы), являющиеся источником поля в воздухе. Но если есть полюс, то поле от него направлено во все стороны, в том числе и внутрь магнетика, так что внутри магнетика , (1.107)
, (1.107) - поле внутри магнетика;
- поле внутри магнетика;  - внешнее поле (поле, создаваемое источником, например, соленоидом);
- внешнее поле (поле, создаваемое источником, например, соленоидом);  - поле, обусловленное полюсами на границах образца (размагничивающее поле).
- поле, обусловленное полюсами на границах образца (размагничивающее поле). , (1.108)
, (1.108) - коэффициент размагничивания (иногда называемый размагничивающим фактором), зависящий при однородном намагничивании только от формы магнетика. Однородно намагничиваются только эллипсоиды, для которых величина
- коэффициент размагничивания (иногда называемый размагничивающим фактором), зависящий при однородном намагничивании только от формы магнетика. Однородно намагничиваются только эллипсоиды, для которых величина  может быть точно определена. В большинстве же случаев тело намагничивается неоднородно,
может быть точно определена. В большинстве же случаев тело намагничивается неоднородно,  и
и  будут в разных точках различны, поэтому пользуются некоторыми усреднёнными значениями
будут в разных точках различны, поэтому пользуются некоторыми усреднёнными значениями  . Для проволоки диаметром
. Для проволоки диаметром  , длиной
, длиной  , намагничиваемой в направлении
, намагничиваемой в направлении  , значения
, значения  приведены в табл. 1.4.
приведены в табл. 1.4. ,
,  ,
,  (соответствующих намагничиванию эллипсоида вдоль осей
(соответствующих намагничиванию эллипсоида вдоль осей  ,
,  ,
,  )имеют достаточно сложный характер, но всегда выполняется
)имеют достаточно сложный характер, но всегда выполняется . (1.109)
. (1.109) можно определить очень просто. Очевидно, что для шара
можно определить очень просто. Очевидно, что для шара  . Для бесконечно длинного цилиндра круглого сечения при его поперечном намагничивании
. Для бесконечно длинного цилиндра круглого сечения при его поперечном намагничивании  .
. . Пусть теперь
. Пусть теперь  и
и  (т.е. очень тонкий вытянутый сфероид, почти проволока), тогда коэффициенты размагничивания можно рассчитать по формулам:
(т.е. очень тонкий вытянутый сфероид, почти проволока), тогда коэффициенты размагничивания можно рассчитать по формулам: , (1.110)
, (1.110) . (1.111)
. (1.111) рассчитанные по (1.110) и приведённые в табл. 1.4 совпадают, начиная примерно с
рассчитанные по (1.110) и приведённые в табл. 1.4 совпадают, начиная примерно с  (в соответствии с условием
(в соответствии с условием  ).
). ,
,  , следовательно
, следовательно ; (1.112)
; (1.112) . (1.113)
. (1.113) , то
, то  (очень длинная проволока, намагничиваемая поперёк).
(очень длинная проволока, намагничиваемая поперёк). . Рассмотрим (рис. 1.39) прямоугольный параллелепипед (полосу), намагничиваемый полем
. Рассмотрим (рис. 1.39) прямоугольный параллелепипед (полосу), намагничиваемый полем  перпендикулярно грани сечения наибольшего размера. Если величина заряда на единицу длины грани есть
перпендикулярно грани сечения наибольшего размера. Если величина заряда на единицу длины грани есть 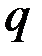 , то напряжённость поля, создаваемого одной гранью на расстоянии
, то напряжённость поля, создаваемого одной гранью на расстоянии  (
(  , где
, где 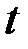 - толщина полосы),
- толщина полосы), .
. , то
, то  .
. расстояние от края
расстояние от края 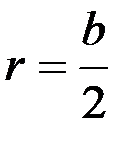 , а
, а .
. , то
, то . (1.114)
. (1.114)