
|
|
Доменная структура ферромагнетиковЕсли бы обменное взаимодействие было единственным видом взаимодействия в ферромагнитном кристалле, то и в отсутствии внешнего магнитного поля ферромагнетик был бы намагничен до насыщения как одно целое. Учет других видов взаимодействий показывает, что энергетически более выгодным оказывается не то состояние, при котором весь кристалл однородно намагничен до насыщения, а состояние, когда ферромагнитный образец разбит на отдельные области (домены) с таким распределением ориентаций самопроизвольной намагниченности в них, чтобы результирующая намагниченность всего образца в целом равнялась нулю.
Рис. 1.27. Разбиение ферромагнитного кристалла на домены, соответствующие уменьшению магнитостатической энергии размагничивающего поля
Первое теоретическое обоснование гипотезы доменов дали Френкель и Дорфман. Кроме обменной они учли только энергию ферромагнетика конечных размеров в собственном размагничивающем поле (1.80). Однако, им удалось не только обосновать разбиение ферромагнетика на домены (рис. 1.27), но и получить полуколичественное уравнение для ширины доменов:
Рис. 1.28. Доменная структура в Рис. 1.29. Тонкая доменная ферромагнетике с одной осью структура ферромагнетика легкого намагничивания (ОЛН)
Эти оценочные расчеты находятся в хорошем качественном согласии с экспериментальными данными. Более строгая теория доменной структуры ферромагнетиков была построена Ландау и Лившицем, которые учли энергию магнитной анизотропии и то обстоятельство, что намагниченность в отдельных доменах ориентируется вдоль осей легкого намагничивания. В случае идеального одноосного ферромагнитного кристалла домены должны иметь форму, изображенную на рисунке 1.28. Вблизи поверхности форма доменов становится такой, чтобы уменьшить энергию размагничивающего поля Ландау и Лившиц нашли также выражение для толщины граничного слоя между доменами, называемого доменной границей, и выяснили закон изменения намагниченности в этом слое. Следует отметить, что наличие переходного граничного слоя граничной толщины
причем
Рис. 1.30. Структура граничного слоя между доменами в ферромагнитном кристалле (а) и зависимость
Для толщины граничного слоя Ландау и Лившиц получили общую формулу
где Для поверхностной плотности энергии граничного слоя теми же авторами получено выражение
Для железа при комнатной температуре
Рис. 1.31. Схема доменной структуры ферромагнетика с тремя осями легкого намагничивания
Кроме описанных выше так называемых 180o-ных границ между доменами, разделяющих области с антипараллельным направлением намагниченности, в ферромагнетиках с несколькими осями легкого намагничивания оказываются возможными (рис. 1.31) еще соседства со взаимно перпендикулярными (или близкими к ним) направлениями спонтанной намагниченности, называемые 90-градусными границами. В реальных кристаллах картина значительно усложняется из-за структурных дефектов и внутренних напряжений. Но граница между доменами всегда располагается так, чтобы вносимое ею увеличение свободной энергии кристалла было минимальным. Это значит, что 180o-ные границы располагаются по местам с минимумами внутренних напряжений, где величина В настоящее время существует ряд хорошо разработанных экспериментальных методов наблюдения и исследования доменной структуры ферромагнетиков. Наиболее часто для изучения доменной структуры используются следующие методы. Метод порошковых фигур. Метод основан на том, что мелкие ферромагнитные частицы притягиваются к полюсам магнитов. Так как в граничном слое между доменами намагниченность поворачивается, образуя составляющую, перпендикулярную к поверхности образца, то тонкий ферромагнитный порошок (Fe2O3), взвешенный в жидкости, оседая на поверхность хорошо отполированного ферромагнетика, будет собираться у доменных границ. Образованные таким образом порошковые фигуры передают картину доменной структуры. На рис. 1.32 приведена картина порошковых осадков, показывающая изменение доменной структуры текстурованного кремнистого железа под действием растягивающих напряжений. Видно, что при растяжении местоположение доменных границ изменилось. Направление самопроизвольной намагниченности стало совпадать с направлением растяжения, поскольку магнитострикция кремнистого железа положительна. Изменилось также и расстояние между границами.
Рис. 1.32. Картины порошковых осадков, выявляющие доменную структуру на поверхности текстурованного кремнистого железа: а – при отсутствии внешних напряжений; б – образец растянут в вертикальном направлении. Метод магнитооптического эффекта Керра. Позволяет наблюдать всю поверхность доменов. Суть его заключается в следующем. Если на намагниченное зеркало падает луч плоскополяризованного света, то при отражении происходит поворот плоскости поляризации на угол, пропорциональный намагниченности зеркала. Так как эффект нечетный (т.е. зависит от знака намагниченности), то, если поляризованный свет, отраженный от полированной поверхности ферромагнитного кристалла, пропустить через анализатор, вследствие различных направлений Процессы намагничивания Сам факт существования доменов позволяет установить типы процессов намагничивания в ферромагнетиках. Как уже упоминалось, ферромагнитный образец в естественном состоянии, в отсутствие внешнего магнитного поля, не имеет результирующей намагниченности. Поэтому
где
Первое слагаемое обусловлено ростом объемов доменов, векторы
При намагничивании реальных материалов в области слабых полей основную роль играют процессы смещения ( Оба эти типа процессов в свою очередь могут быть обратимыми и необратимыми. Последний тип процессов определяет собой все явления магнитного гистерезиса. Смещение доменных границ. Эффект Баркгаузена. Под влиянием внешних воздействий условия равновесия границ между магнитными фазами меняются, и границы начинают смещаться. Это смещение будет продолжаться до тех пор, пока не установится новое равновесное состояние. При смещении границ в ферромагнетике возникают вихревые токи, магнитное поле которых противодействует этому смещению. В результате в каждом случае устанавливается конечная скорость смещения. Однако если процесс намагничивания вести достаточно медленно (квазистатически), то этими кинетическими эффектами можно пренебречь и считать, что граница смещается синхронно с изменением внешнего магнитного поля. При процессах смещения положение граничной зоны между различными магнитными фазами определяется в каждый момент равновесием между внешними и внутренними силами. Внешние силы только тогда приводят к смещению границ, когда они создают различную плотность внешней свободной энергии по обе стороны от границы. Если ферромагнетик подвергнут действию только внешнего магнитного поля, то разность плотностей свободной энергии этого поля
где Поворот намагниченности на 180о при смещении 180о-ной границы не требует затраты работы против механических напряжений в силу четности магнитострикционных эффектов. Поэтому вся работа внешнего поля сводится к компенсации увеличения поверхностной свободной энергии Совсем иной характер носят смещения 90о-ных границ. Последние возникают в тех местах кристалла, где напряжения меняют знак. Поэтому при смещении этих границ большая часть работы внешнего магнитного поля идет не на компенсацию изменения поверхностной энергии Таким образом, основными причинами самого существования технической кривой намагничивания (по крайней мере, её начального участка) являются: 1) неоднородности состава, искажения кристаллической решетки, неоднородности внутренних напряжений; 2) изменение величины поверхностных слоев между магнитными фазами. Эти причины требуют затраты конечной энергии со стороны внешнего магнитного поля для смещения границ между доменами, т.е. для изменения величины результирующей намагниченности ферромагнетика. До сих пор неявно предполагалось, что смещения границ идут обратимо, т.е., что при обратном квазистатическом уменьшении внешнего поля границы должны смещаться в обратном направлении через те же места в кристалле и при поле В качестве примера рассмотрим движение 180о-ной границы. Поверхностная энергия
Рис. 1.33. Схема доменной структуры
границ между доменами. Пусть граничные зоны лежат в плоскости, параллельной
В левой части (1.93) стоит выигрыш магнитной энергии, приходящейся на единицу поверхности граничной зоны, а в правой части изменение энергии граничной зоны. В данном случае давление внешнего поля на границу, согласно (1.92), равно
которое направлено против давления
равно ему по абсолютной величине.

Рис. 1.34. Схема необратимого смещения доменной границы (скачок Баркгаузена)
Соотношения (1.94) или (1.95) дают связь между равновесными значениями поля При процессах смещения положение граничной зоны между различными магнитными фазами определяется в каждый момент равновесием между внешними и внутренними силами. Внешние силы только тогда приводят к смещению границ, когда они создают различную плотность внешней свободной энергии по обе стороны от границы. При этом поле достигает некоторого определенного значения Переход границы из Подобным же образом можно проанализировать обратимое и необратимое смещения граничной зоны для случая 90о-ного соседства. Всё отличие будет заключаться в том, что в правой части (1.93) появится ещё член, соответствующий изменению магнитоупругой энергии напряжений, вызванному поворотом спонтанной намагниченности при смещении граничной зоны 90о-ного типа. Этот член, как правило, больше, чем рассмотренный в (1.93), и поэтому он определяет весь процесс смещения 90о-ной границы. Порядок величины этой энергии равен В обычных технических материалах имеется большой статистический разброс значений критического поля
Рис. 1.35. Эффект Баркгаузена
Дополнительно заметим, что причиной эффекта Баркгаузена могут быть также необратимые процессы вращения и процессы зародышеобразования (зарождения в намагниченном ферромагнетике при уменьшении поля доменов с противоположным по отношению ко всему объему направлением самопроизвольной намагниченности). Основные области кривой намагничивания. По характеру процессов намагничивания кривую намагничивания условно можно разбить на пять участков (рис. 1.36). Участок I характеризуется постоянной восприимчивостью (проницаемостью), то есть Участок II носит название области Релея. Намагничивание на этом участке в основном осуществляется за счёт смещения доменных границ. Для этой области кривой намагничивания справедлив закон Релея (1.96), который
Рис. 1.36. Основные области кривой намагничивания
выполняется практически для всех ферромагнетиков (у некоторых эта область может отсутствовать). Намагниченность в области Релея определяется как
где Участок III характеризуется высоким значением магнитной восприимчивости (проницаемости). В этой области намагниченность меняется большими скачками Баркгаузена, вызванными необратимым смещением доменных границ. Для многоосных магнитотвёрдых материалов кроме процессов смещения в этом диапазоне полей характерны процессы скачкообразного вращения векторов намагниченности. Участок IV. Восприимчивость постепенно уменьшается. Процесс намагничивания на этом участке осуществляется в основном за счёт вращения векторов спонтанной намагниченности на направление внешнего магнитного поля. Работа по повороту векторов спонтанной намагниченности на направление действующего поля затрачивается на преодоление кристаллографической анизотропии, которая стремится удержать векторы спонтанной намагниченности в направлении лёгкого намагничивания. Процессы вращения происходят преимущественно обратимо. Для IV участка справедлив закон приближения к насыщению
где Участок V – область парапроцесса. Процессы смещения и вращения закончены. На этом участке в сильных магнитных полях незначительное увеличение намагниченности связано с дополнительной ориентацией спиновых магнитных моментов в направлении приложенного поля. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 , где
, где  - линейный размер образца, а
- линейный размер образца, а  ~ 10-4 см. Это значит, что при размерах образца L ~ 1 см ширина доменов должна быть
~ 10-4 см. Это значит, что при размерах образца L ~ 1 см ширина доменов должна быть  ~ 10-2 см.
~ 10-2 см. даже за счет некоторого увеличения энергии магнитной анизотропии
даже за счет некоторого увеличения энергии магнитной анизотропии  . Это ведет к образованию граничных доменов в виде трехгранных призм, в которых направление
. Это ведет к образованию граничных доменов в виде трехгранных призм, в которых направление  перпендикулярно оси легкого намагничивания, и к замыканию магнитного потока, что соответствует минимуму свободной энергии кристалла. По мере роста поверхности трехгранных областей более выгодной становится форма доменов, изображенная на рис 1.29.
перпендикулярно оси легкого намагничивания, и к замыканию магнитного потока, что соответствует минимуму свободной энергии кристалла. По мере роста поверхности трехгранных областей более выгодной становится форма доменов, изображенная на рис 1.29. увеличивает энергию магнитной анизотропии
увеличивает энергию магнитной анизотропии  , которая растет с ростом
, которая растет с ростом  . С этой точки зрения выгоднее было бы отсутствие протяженной доменной границы, т.е. скачок вектора
. С этой точки зрения выгоднее было бы отсутствие протяженной доменной границы, т.е. скачок вектора  от одного направления к противоположному. Однако такой скачок невыгоден с точки зрения обменных сил, так как он привел бы к значительному росту обменной энергии. Конкуренцией между этими двумя взаимодействиями и определяется толщина
от одного направления к противоположному. Однако такой скачок невыгоден с точки зрения обменных сил, так как он привел бы к значительному росту обменной энергии. Конкуренцией между этими двумя взаимодействиями и определяется толщина  переходного слоя и характер изменения намагниченности
переходного слоя и характер изменения намагниченности  в этом слое, показанный на рис 1.30. В переходном слое
в этом слое, показанный на рис 1.30. В переходном слое  постепенно поворачивается, при этом проекция намагниченности
постепенно поворачивается, при этом проекция намагниченности  на поверхность образца меняется по закону
на поверхность образца меняется по закону  , где
, где , (1.86)
, (1.86) – расстояние от середины граничного слоя.
– расстояние от середины граничного слоя.
 от x (б)
от x (б) , (1.87)
, (1.87) – обменный интеграл;
– обменный интеграл;  – эффективная константа магнитной анизотропии, зависящая от естественной кристаллографической анизотропии и напряжений; параметр
– эффективная константа магнитной анизотропии, зависящая от естественной кристаллографической анизотропии и напряжений; параметр  имеет размерность длины и порядок постоянной кристаллической решетки. При комнатной температуре (1.87) дает для
имеет размерность длины и порядок постоянной кристаллической решетки. При комнатной температуре (1.87) дает для  величину порядка 10-6 см.
величину порядка 10-6 см. . (1.88)
. (1.88) ~ 1 эрг/см2. Заметим, что величина
~ 1 эрг/см2. Заметим, что величина  и ее зависимость от координат играют важнейшую роль в протекании процессов намагничивания, особенно в процессах смещения доменных границ.
и ее зависимость от координат играют важнейшую роль в протекании процессов намагничивания, особенно в процессах смещения доменных границ. минимальна и, следовательно, минимальна величина
минимальна и, следовательно, минимальна величина  . Девяностоградусные границы располагаются преимущественно там, где напряжения меняют знак, так как изменению знака внутренних напряжений соответствует изменение направлений осей легкого намагничивания, которые определяют направления намагниченности
. Девяностоградусные границы располагаются преимущественно там, где напряжения меняют знак, так как изменению знака внутренних напряжений соответствует изменение направлений осей легкого намагничивания, которые определяют направления намагниченности  в соседних доменах.
в соседних доменах.
 в соседних доменах последние будут освещены по-разному. Благодаря этому доменную структуру можно четко наблюдать визуально.
в соседних доменах последние будут освещены по-разному. Благодаря этому доменную структуру можно четко наблюдать визуально. , (1.89)
, (1.89) - объем i-го домена,
- объем i-го домена,  - угол между вектором намагниченности i-го домена и любым зафиксированным направлением в образце. Если включить внешнее магнитное поле
- угол между вектором намагниченности i-го домена и любым зафиксированным направлением в образце. Если включить внешнее магнитное поле  , то образец начинает намагничиваться и вдоль направления
, то образец начинает намагничиваться и вдоль направления  появляется отличный от нуля результирующий магнитный момент
появляется отличный от нуля результирующий магнитный момент  тела. Этот момент в общем случае складывается из двух частей:
тела. Этот момент в общем случае складывается из двух частей: . (1.90)
. (1.90) которых направлены относительно
которых направлены относительно  в доменах. Эти процессы принято называть процессами вращения. Таким образом, восприимчивость ферромагнетика можно представить в виде суммы восприимчивостей двух типов процессов – смещения и вращения:
в доменах. Эти процессы принято называть процессами вращения. Таким образом, восприимчивость ферромагнетика можно представить в виде суммы восприимчивостей двух типов процессов – смещения и вращения: (1.91)
(1.91) ). В полях больших, чем поле, соответствующее максимуму на кривой
). В полях больших, чем поле, соответствующее максимуму на кривой  , наоборот, основную роль играют процессы вращения (
, наоборот, основную роль играют процессы вращения (  ).
). между доменами k и i вызывает давление на границу между ними:
между доменами k и i вызывает давление на границу между ними: , (1.92)
, (1.92) и
и  – намагниченность k-го и i-го доменов.Это “внешнее” давление должно уравновешиваться внутренними силами.
– намагниченность k-го и i-го доменов.Это “внешнее” давление должно уравновешиваться внутренними силами. . Изменение этой последней может происходить, во-первых, вследствие перемещения граничной зоны в те места кристалла, где
. Изменение этой последней может происходить, во-первых, вследствие перемещения граничной зоны в те места кристалла, где  получает иное значение и, во-вторых, ввиду изменений в результате смещения суммарной величины граничной поверхности между рассматриваемыми доменами.
получает иное значение и, во-вторых, ввиду изменений в результате смещения суммарной величины граничной поверхности между рассматриваемыми доменами. , а на увеличение магнитоупругой объемной энергии. Последнее вызывается тем, что при смещении 90о-ных границ “захваченные” смещением участки кристалла намагничиваются вдоль тех осей легчайшего намагничивания, которые в силу действия растяжения или сжатия являются энергетически более выгодными. Это и должно быть скомпенсировано работой внешнего поля.
, а на увеличение магнитоупругой объемной энергии. Последнее вызывается тем, что при смещении 90о-ных границ “захваченные” смещением участки кристалла намагничиваются вдоль тех осей легчайшего намагничивания, которые в силу действия растяжения или сжатия являются энергетически более выгодными. Это и должно быть скомпенсировано работой внешнего поля. занять свои исходные положения. Однако наряду с обратимыми смещениями могут происходить и необратимые процессы смещения.
занять свои исходные положения. Однако наряду с обратимыми смещениями могут происходить и необратимые процессы смещения. вследствие неоднородностей внутренних напряжений и дефектов кристаллической решетки является функцией координат. Предположим, для простоты, что домены имеют форму плоскопараллельных слоев. Этим мы исключаем эффект изменения поверхностной энергии в результате увеличения суммарной поверхности
вследствие неоднородностей внутренних напряжений и дефектов кристаллической решетки является функцией координат. Предположим, для простоты, что домены имеют форму плоскопараллельных слоев. Этим мы исключаем эффект изменения поверхностной энергии в результате увеличения суммарной поверхности (рис. 1.33); намагниченность направлена вдоль оси
(рис. 1.33); намагниченность направлена вдоль оси  или
или  , а поверхностная энергия
, а поверхностная энергия  является функцией только координаты х. Тогда, если поле параллельно легчайшей оси
является функцией только координаты х. Тогда, если поле параллельно легчайшей оси  , условие равновесия границы при бесконечно малом смещении
, условие равновесия границы при бесконечно малом смещении  будет иметь вид:
будет иметь вид: . (1.93)
. (1.93) (так как
(так как  и
и  ). Величина
). Величина  эквивалентна некоторому внутреннему давлению “поверхностного натяжения границы”.
эквивалентна некоторому внутреннему давлению “поверхностного натяжения границы”. (1.94)
(1.94) и в случае равновесия,
и в случае равновесия, , (1.95)
, (1.95)

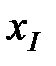
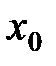









 , которое доводит смещение границы до координаты
, которое доводит смещение границы до координаты  , и градиентом поверхностной энергии
, и градиентом поверхностной энергии  . В исходном состоянии минимум
. В исходном состоянии минимум  находится при
находится при  , т.е.
, т.е.  . Очевидно, что обратимое смещение будет происходить до тех пор, пока граница, выйдя из своего равновесного положения
. Очевидно, что обратимое смещение будет происходить до тех пор, пока граница, выйдя из своего равновесного положения  (рис. 1.34), не достигнет точки
(рис. 1.34), не достигнет точки  , которой соответствует ближайший максимум
, которой соответствует ближайший максимум  (или точки
(или точки  , которой соответствует экстремум величины –
, которой соответствует экстремум величины –  , при обратном направлении поля).
, при обратном направлении поля). играющего роль критического поля. После достижения поля
играющего роль критического поля. После достижения поля  , граница может продолжать свое смещение без дальнейшего увеличения внешнего поля, вплоть до точки
, граница может продолжать свое смещение без дальнейшего увеличения внешнего поля, вплоть до точки  , ибо при этом внутреннее давление
, ибо при этом внутреннее давление  делается отрицательным. Таким образом, происходит скачок Баркгаузена. Этот скачок протекает не мгновенно, а с конечной скоростью, величина которой определяется тормозящим действием магнитного поля вихревых токов, создаваемых при смещении границы. В результате скачка Баркгаузена граница занимает положение
делается отрицательным. Таким образом, происходит скачок Баркгаузена. Этот скачок протекает не мгновенно, а с конечной скоростью, величина которой определяется тормозящим действием магнитного поля вихревых токов, создаваемых при смещении границы. В результате скачка Баркгаузена граница занимает положение  . При дальнейшем увеличении поля граница снова смещается обратимо вплоть до следующего более высокого максимума
. При дальнейшем увеличении поля граница снова смещается обратимо вплоть до следующего более высокого максимума  в точке
в точке  , при условии, что антипараллельный домен, объем которого уменьшается при смещении границы, распространяется за точку
, при условии, что антипараллельный домен, объем которого уменьшается при смещении границы, распространяется за точку  , в которой в исходном состоянии могла быть другая граница.
, в которой в исходном состоянии могла быть другая граница. в
в  является необратимым. Действительно, если после достижения точки
является необратимым. Действительно, если после достижения точки  уменьшать величину магнитного поля, например, до прежнего его значения, соответствовавшего положению границы в точке
уменьшать величину магнитного поля, например, до прежнего его значения, соответствовавшего положению границы в точке  , то граница отнюдь не вернется в эту точку, а обратимо перейдет из точки
, то граница отнюдь не вернется в эту точку, а обратимо перейдет из точки  в точку
в точку  . Чтобы вернуться в точку
. Чтобы вернуться в точку  , придется произвести довольно сложную операцию перемагничивания. Для этого нужно выключив магнитное поле перейти в точку
, придется произвести довольно сложную операцию перемагничивания. Для этого нужно выключив магнитное поле перейти в точку  , затем приложив поле обратного знака и увеличивая его пройти положения
, затем приложив поле обратного знака и увеличивая его пройти положения 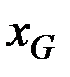 ,
, 
 ,
,  , снова выключить поле, включить поле в первоначальном направлении и увеличивать его до скачкообразного перемещения границы из положения
, снова выключить поле, включить поле в первоначальном направлении и увеличивать его до скачкообразного перемещения границы из положения  в положение
в положение  .
.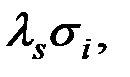 где
где  - линейная магнитострикция насыщения, а
- линейная магнитострикция насыщения, а  - величина внутренних или внешних напряжений. Таким образом, критическое поле в случае 90о-ной границы определяется значением максимумов напряжений
- величина внутренних или внешних напряжений. Таким образом, критическое поле в случае 90о-ной границы определяется значением максимумов напряжений  , встречающихся на пути смещающейся границы.
, встречающихся на пути смещающейся границы. , обусловленный беспорядочным распределением неоднородностей внутренних напряжений. Этот разброс
, обусловленный беспорядочным распределением неоднородностей внутренних напряжений. Этот разброс  приводит к “сглаживанию” кривой намагничивания. Более тщательные эксперименты показывают ”ступенчатый” (рис. 1.35) характер кривой намагничивания (эффект Баркгаузена), причем вертикальные части этих ступенек соответствуют скачкам Баркгаузена для определенных значений критических полей.
приводит к “сглаживанию” кривой намагничивания. Более тщательные эксперименты показывают ”ступенчатый” (рис. 1.35) характер кривой намагничивания (эффект Баркгаузена), причем вертикальные части этих ступенек соответствуют скачкам Баркгаузена для определенных значений критических полей. (
(  ). Намагничивание ферромагнетика на этом участке кривой намагничивания осуществляется за счёт обратимого (упругого) смещения доменных границ.
). Намагничивание ферромагнетика на этом участке кривой намагничивания осуществляется за счёт обратимого (упругого) смещения доменных границ. B
B
 , (1.96)
, (1.96) - коэффициент Релея. Второй член в уравнении (1.96) представляет вклад необратимых процессов при намагничивании.
- коэффициент Релея. Второй член в уравнении (1.96) представляет вклад необратимых процессов при намагничивании. , (1.97)
, (1.97) - намагниченность насыщения,
- намагниченность насыщения, 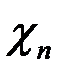 - восприимчивость парапроцесса,
- восприимчивость парапроцесса,  ,
,  ,
,  , … - постоянные коэффициенты, определяющие вклад различных структурных факторов (точечные дефекты, дислокации и т.д.), влияющих на процесс намагничивания. Выражение (1.97) справедливо для полей, при которых ферромагнетик намагничен до технического насыщения (
, … - постоянные коэффициенты, определяющие вклад различных структурных факторов (точечные дефекты, дислокации и т.д.), влияющих на процесс намагничивания. Выражение (1.97) справедливо для полей, при которых ферромагнетик намагничен до технического насыщения (  ).
).