
|
|
Намагничивания вдоль кристаллографических осей.
В ферромагнитных кристаллах существуют оси “легкого” и “трудного” намагничивания. На рис. 1.26 показаны кривые намагничивания для разных кристаллографических осей железа Fe (объемноцентрированная решетка), никеля Ni (гранецентрированная) и кобальта Co (гексагональная). Спонтанная (самопроизвольная) намагниченность в каждом домене ориентируется вдоль направления легкого намагничивания. Чтобы намагнитить ферромагнетик в более трудном направлении, необходимо затратить определенную энергию, пропорциональную площади между этими кривыми и являющуюся мерой энергии естественной кристаллографической магнитной анизотропии. В некоторых случаях анизотропия может отсутствовать, например, для сплава Fe-Ni с 70% Ni. Энергию магнитной анизотропии кристалла кубической симметрии (железо, никель) можно выразить следующим образом:
где Можно считать, что существует некоторое поле анизотропии Магнитоупругая энергия. При намагничивании ферромагнетиков наблюдается изменение их линейных или объёмных размеров. Это явление получило название соответственно линейной или объемной магнитострикции. Относительное удлинение Изменению формы каждого домена в многодоменном кристалле препятствуют другие домены, результатом чего является увеличение упругих напряжений. Энергия тела увеличивается на величину магнитоупругой энергии. Если обозначить среднюю по кристаллу магнитострикцию
Железо, намагничиваясь в сравнительно слабых полях, несколько удлиняется, при этом поперечное сечение образца уменьшается (положительная магнитострикция). Отсюда на основе принципа Вант-Гоффа и Ле-Шателье о противодействии системы действующим на неё силам, следует, что сжатие железного образца будет препятствовать его намагничиванию, а растяжение – способствовать. При растяжении мы получим увеличение начальной магнитной проницаемости. Для никелевого стержня получается обратная картина, так как при намагничивании его длина сокращается при некотором расширении поперечного сечения (отрицательная магнитострикция). При положительной магнитострикции направление упругого растяжения является направлением легкого намагничивания, если работа, расходуемая на преодоление препятствий, связанных с магнитострикцией, преобладает над работой преодоления препятствий, связанных с кристаллической магнитной анизотропией. Растянутая поликристаллическая проволока в магнитном отношении приближается к свойствам монокристалла. Очевидно, что сжимающие напряжения в данном случае уменьшили бы проницаемость и повысили бы коэрцитивную силу. В случае отрицательной магнитострикции (например, в никеле) упругое сжатие облегчало бы процесс намагничивания и размагничивания, а растяжение затрудняло бы эти процессы. При намагничивании, например, растянутого образца никеля или сжатого образца железа возникает дополнительная энергия, равная приблизительно Можно считать, что общая энергия анизотропии складывается из энергии магнитной кристаллографической анизотропии и магнитоупругой энергии. Под влиянием кристаллической анизотропии и внешних сил устанавливается наивыгоднейшее направление самопроизвольного намагничивания (направление вектора
которую принято называть эффективной константой магнитной анизотропии. Она складывается из энергий кристаллической анизотропии ( Понятие о Магнитостатическая энергия. Имеются две разновидности магнитостатической энергии. Сначала рассмотрим энергию взаимодействия постоянного магнитного поля с постоянным магнитным моментом
где минус указывает на то, что энергия Вторая разновидность – это энергия, связанная с образованием магнитных полюсов на концах намагниченного ферромагнетика конечных размеров. В этом случае при намагничивании внутри тела ферромагнетика создается внутреннее поле
т.е. оно тем больше, чем сильнее намагничено тело. Можно сказать, что Дополнительная энергия, связанная с образованием магнитных полюсов на границах намагниченного ферромагнетика конечных размеров, имеет место даже в отсутствие внешнего поля. Например, дополнительная энергия намагниченного призматического образца конечных размеров равна:
где Особенности намагничивания тел конечных размеров более подробно будут рассмотрены далее. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 , (1.80)
, (1.80)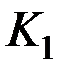 ,
,  – константы кристаллографической магнитной анизотропии, а
– константы кристаллографической магнитной анизотропии, а  – направляющие косинусы углов между направлением намагниченности
– направляющие косинусы углов между направлением намагниченности  и основными кристаллографическими направлениями решетки.
и основными кристаллографическими направлениями решетки.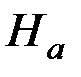 , которое препятствует отклонению магнитных моментов ферромагнетика от направления лёгкого намагничивания, причем
, которое препятствует отклонению магнитных моментов ферромагнетика от направления лёгкого намагничивания, причем 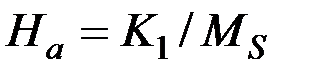 .
.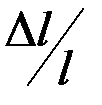 может достигать величин порядка 10-5- 10-3. Наблюдается также обратное явление: изменение намагниченности ферромагнитного тела при деформации (магнитоупругий эффект).
может достигать величин порядка 10-5- 10-3. Наблюдается также обратное явление: изменение намагниченности ферромагнитного тела при деформации (магнитоупругий эффект). , а
, а  - модуль упругости (средняя величина, не зависящая от направления в кристалле), то произведение этих величин
- модуль упругости (средняя величина, не зависящая от направления в кристалле), то произведение этих величин  есть напряжение, и тогда магнитоупругая энергия равна:
есть напряжение, и тогда магнитоупругая энергия равна: . (1.81)
. (1.81) (с точностью до цифрового коэффициента порядка единицы), где
(с точностью до цифрового коэффициента порядка единицы), где  - напряжение от внешних сил, а
- напряжение от внешних сил, а 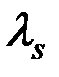 - магнитострикция насыщения. Эта энергия играет большую роль при очень сильных напряжениях или очень маленькой кристаллографической анизотропии, т.е. при
- магнитострикция насыщения. Эта энергия играет большую роль при очень сильных напряжениях или очень маленькой кристаллографической анизотропии, т.е. при 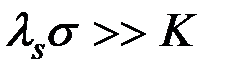 . Здесь учитывается магнитострикция насыщения
. Здесь учитывается магнитострикция насыщения 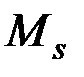 ) в каждом домене, соответствующее минимуму энергии, и изменение этого направления согласно (1.80) и (1.81) связано с дополнительной энергией
) в каждом домене, соответствующее минимуму энергии, и изменение этого направления согласно (1.80) и (1.81) связано с дополнительной энергией , (1.82)
, (1.82) ) и магнитоупругой энергии (
) и магнитоупругой энергии (  ). Причем
). Причем  и
и  - числовые коэффициенты порядка единицы.
- числовые коэффициенты порядка единицы. может быть распространено также на ферромагнетик, на который внешние силы не действуют. В таком случае
может быть распространено также на ферромагнетик, на который внешние силы не действуют. В таком случае  является величиной внутренних напряжений, возникающих вследствие несовершенства кристаллического строения.
является величиной внутренних напряжений, возникающих вследствие несовершенства кристаллического строения. . Такое взаимодействие в чистом виде можно представить себе, если в поле
. Такое взаимодействие в чистом виде можно представить себе, если в поле  поместить однодоменную частицу с моментом (намагниченностью)
поместить однодоменную частицу с моментом (намагниченностью)  и принять, что при любом
и принять, что при любом 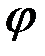 (угол между направлениями
(угол между направлениями  и
и  ) длина вектора
) длина вектора  (1.83)
(1.83) минимальна, если
минимальна, если  ), и максимальна, если антипараллельны (
), и максимальна, если антипараллельны ( 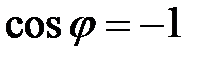 ). Отрицательное значение
). Отрицательное значение 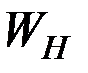 соответствует тому случаю, когда общая свободная энергия системы уменьшается благодаря магнитостатической энергии.
соответствует тому случаю, когда общая свободная энергия системы уменьшается благодаря магнитостатической энергии. , направленное против внешнего магнитного поля
, направленное против внешнего магнитного поля  . Размагничивающее поле
. Размагничивающее поле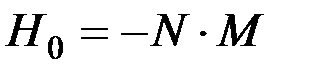 , (1.84)
, (1.84) противодействует намагничиванию тела. Величина
противодействует намагничиванию тела. Величина  носит название коэффициента размагничивания (размагничивающего фактора) и главным образом зависит от отношения длины
носит название коэффициента размагничивания (размагничивающего фактора) и главным образом зависит от отношения длины  ферромагнитного тела к его диаметру
ферромагнитного тела к его диаметру 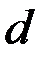 .
. , (1.85)
, (1.85) - это некоторая эффективная величина, так как такой образец намагничен неоднородно.
- это некоторая эффективная величина, так как такой образец намагничен неоднородно.