
|
|
Глава 5. Определение параметров составляющих сложного сигнала.Рассмотрим алгоритм разделения сложного сигнала на составляющие, имеющие лоренцевскую форму при помощи некоторых преобразований, сводящих нелинейную задачу минимизации к решению линейных уравнений [13], Необходимая априорная информация – количество элементарных составляющих. Пусть наблюдаемый сигнал можно представить в виде:
Здесь
получим
Здесь и далее штрих у знака произведения в правой части означает, что из произведения исключен множитель с i=j. Выражение (5.3) можно записать в виде:
Корни
Введем новые переменные
С учетом равенств (5.6) и (5.7) выражение (5.1) может быть записано в виде:
Выражение (5.8) представляет собой систему линейных уравнений с 4m-1 неизвестными: 2m неизвестных xj и 2m-1 неизвестных zk. Система может быть решена по известным значениям F(w i) в 4m-1 точках. Если xi определены, то равенства (25) определяют полином порядка 2m относительно переменных
и связанных с ними параметров
Переменные
где матрица Lij определяется выражением
Корни полинома (5.9) могут быть определены с помощью метода Берстоу [14], позволяющего определить комплексные корни многочлена. Для устранения шумов в данном случае могут быть реализованы две возможности: либо предварительное сглаживание экспериментального спектра на основе метода статистической регуляризации, либо решение системы уравнений (5.8) с использованием метода регуляризации (алгоритмы описаны выше). Для анализа эффективности работы алгоритма проведем численные эксперименты. Основой модельного сигнала выбираем сложный сигнал, в первом случае состоящий из двух составляющих, во втором случае состоящий из трех составляющих. В обоих случаях составляющие сигнала будут иметь лоренцевскую форму, характерную для прикладной спектроскопии, параметр Файл-сценарий для получения параметров составляющих сложного сигнала: %Определение параметров составляющих сложного сигнала %a,b,c - параметры лоренцианов:a-амплитуда,b-положение центра,c-полуширина %w1,w2-границы интервала измерений,err-уровень ошибок clear a=[1 2];b=[1 2];c=[3 9]; m=2; n=2; % a=[1 2 1];b=[1 1 1];c=[3 8 12]; %для трех лоренцианов % m=3; n=3; w1=0; w2=13; err=0.05; epse=0.000001; [ft,fe,w,dw]=testf(a,b,c,m,n,w1,w2,err); %формирование тестовых функции, %ft-точная функция, %fe-экспериментальная,dw-шаг, %w-ось абсцисс(для графика) %m-количество составляющих(точное) %n-количество составляющих(априорно задаваемое) [matr1,fi1,x01]=vspom(n,w,fe); [y1]=algorithm2(matr1,fi1,x01,epse); [a1,b1,c1]=consists(y1,n,w,fe,epse) s1=sigma(ft,a1,b1,c1,n,w1,w2) k=eye(4*n-1); [dif,omega,ww,v,h]=matrixs(4*n-1,err,dw); %матрицы:dif-дифференцирования(2 порядка) %omega-стабилизатор, %ww-информационная матрица, %v-ковариационная матрица ошибок, alf=alfa(fe,v,k,omega); %параметр регуляризации(одношаговая оценка) ff=inv(k'*ww*k+alf*omega)*k'*ww*fe'; [matr2,fi2,x02]=vspom(n,w,ff); [y2]=algorithm2(matr2,fi2,x01,epse); [a2,b2,c2]=consists(y2,n,w,ff,epse) s2=sigma(ft,a2,b2,c2,n,w1,w2) Отметим, что для отыскания величин y,y1,y2 мы применили алгоритм 2, а не алгоритм 4, дающий неотрицательное решение, так как при неотрицательном значении y,y1,y2 мы бы получили некоторые отрицательные значения составляющих b и c. Файл-функция для формирования модельной функции и «экспериментальных данных»: function [ft,fe,w,dw]=testf(a,b,c,m,n,w1,w2,err) t=4*n-1; %t=100; dw=(w2-w1)/t; ft=zeros(1,t); for i=1:t w(i)=w1+dw*i; end for i=1:t for j=1:m ft(i)=ft(i)+a(j)/((w(i)-c(j))^2+b(j)^2); end end fe=ft+(randn(t,1)*err)'; Файл-функция (вспомогательная): function [matr,fi,x]=vspom(n,w,f) for i=1:(4*n-1) for j=1:2*n matr(i,j)=f(i)*(w(i)^(2*n-j)); end for j=(2*n+1):(4*n-1) matr(i,j)=-w(i)^(4*n-1-j); end end for i=1:(4*n-1) fi(i)=-f(i)*(w(i)^(2*n)); end fi=fi'; x=zeros(1,4*n-1); Файл-функция для определения составляющих: function[a,b,c]=consists(y,n,w,f,epse) for i=1:2*n x(i)=y(i); end for i=(2*n+1):(4*n-1) z(i-2*n)=y(i); end p=[1 x]; r=roots(p); r=sort(r); for i=1:n Wi1(i)=r(2*i); Wi2(i)=r(2*i-1); end c=real(Wi1); b=imag(Wi1); for i=1:n for j=1:n l(i,j)=1/((w(j)-Wi1(i))*(w(j)-Wi2(i))); end end l=l'; x0=zeros(1,n); for i=1:n ff(i)=f(i); end ff=ff'; a=algorithm2(l,ff,x0,epse); a=a'; Величина среднеквадратичного отклонения
где Файл-функция для определения величины среднеквадратичного отклонения: function [s]=sigma(f,a,b,c,n,w1,w2) dw=(w2-w1)/n; for i=1:n w(i)=w1+dw*i; end ff=zeros(1,n); for i=1:n for j=1:n ff(i)=ff(i)+a(j)/((w(i)-c(j))^2+b(j)^2); end end s=0; for i=1:n s=s+(f(i)-ff(i))^2; end s=(1/n)*s; При
Рис. 8. Зависимость среднеквадратичной ошибки Следует отметить, что с увеличением числа составляющих m несколько возрастает среднеквадратичная ошибка восстановления параметров (рис. 1 – кривые 3 и 4 для m=3). Однако и в этом случае использование методов регуляризации значительно повышает точность решения. Данный метод очень чувствителен к задаваемому априорно количеству составляющих и если n задано неверно, то решение может стать бессмысленным. Для иллюстрации этого факта мы построили таблицу, содержащую значения восстановленных параметров для сложного сигнала из трех лоренциан в зависимости от количества априорно задаваемых кривых:
Таб. 3. Значения восстановленных параметров для сложного сигнала из трех лоренциан в зависимости от количества априорно задаваемых кривых. Ошибка составляла 0,05% от максимального значения интенсивности контура. Истинные значения параметров. Решение также становится бессмысленным при вариации формы элементарных кривых (т.е. если элементарная кривая, задаваемая в ходе математического эксперимента, несколько отличается от лоренцовской, что объясняется плохой обусловленностью системы). Некоторые результаты приведены в таблице 4.
Таб. 4. Значения восстановленных параметров для сложного сигнала из трех составляющих. Ошибка составляла 0,01% от максимального значения интенсивности контура. Форма элементарных составляющих задавалась в виде Как видим, даже небольшая вариация формы кривой (в знаменателе вместо Следует заметить, что с увеличением числа составляющих m несколько возрастает среднеквадратичная ошибка восстановления параметров (рис. 8, кривые 3 и 4 для m=3). Однако и в этом случае использование методов регуляризации значительно повышает точность решения. Была проанализирована точность определения параметров элементарных составляющих в зависимости от расстояний между их максимумами. Некоторые результаты представлены в таблице 5.
Таб. 5. Восстановление параметров при разных расстояниях между максимумами составляющих. Набрасываемая ошибка составляет 0,5% от максимального значения. Видно, что предлагаемый метод позволяет получить достаточно точные значения параметров даже для близко сдвинутых элементарных кривых.
Литература
1. Дьяконов В.П. MATLAB 6:учебный курс. СПб: Питер, 2001. – 592 с. 2. Салахов М.Х., Щербакова Н.К. MATLAB-пакет прикладных программ для решения обратных задач спектроскопии (Методические указания). Казань, Изд-во КГУ,1993. – 32 с. 3. Турчин В.Ф., Козлов В.П., Малкевич М.С. Использование методов математической статистики для решения некорректных задач // УФН, 1970, т. 102, вып. 3. – С. 345-386 (1983). 4. Тихонов А.Н., Арсенин В.Я. Методы решения некорректных задач. 2-е изд. М.: Наука, 1979. – 200 c. 5. Грачев И.Д., Салахов М.Х., Фишман И.С. Статистическая регуляризация при обработке эксперимента в прикладной спектроскопии. Казань: Изд-во КГУ, 1986. – 180 с. 6. Василенко Г.И. Теория восстановления сигналов. М.: Советское радио, 1979. 7. Грачев И.Д., Салахов М.Х., Щербакова Н.К. Проекционный алгоритм сглаживания экспериментальных данных // Автометрия, 1989, № 4. – С. 76-81. 8. Хермен Г. Восстановление изображений по проекциям. М.: Мир, 1983. 9. Брэгман Л.М. Нахождение общей точки выпуклых множеств методом последовательного проектирования // Докл. АН СССР. Серия Матем., 1965, т. 162, № 3. – С. 487-490. 10. Фазылов В.Р. Один общий метод отыскания точки выпуклого множества // Изв. вузов. Матем., 1983, № 6. – С. 43-51. 11. Фазылов В.Р. Метод опорных векторов с составным шагом // Сеточные методы для краевых задач и приложения: (Матер. 4 Всеросс. сем., г. Казань, 13-16 сент. 2002 г.). Казань: Казан. матем. об-во, 2002. – С. 106-109. 12. Волков Е.А. Численные методы.М.:Наука,1987,с.75. 13. Нигматуллин Р.Р., Салахов М.Х., Щербакова Н.К. Разделение сложного спектра на лоренцевские составляющие.// Журнал прикладной спектроскопии, -1988-т.49. №5 с.-820 14. Хемминг Р.В. Численные методы. М.: Наука, 1972, 400 с. 15. Салахов М.Х, Харинцев С.С. Математическая обработка и интерпретация математического эксперимента. Казань: Изд-во КГУ, 2000г., 142 с. 16. Hadamard J. Sur les problemes aux derives particles et leur significations physiques, Bull. Univ. Prinston.-1902.-V.13.-P.49. 17. Hadamard J. Le probleme de Gauchy et les equations aux derivees partielles lineaires hiberboliques.-Paris. Hermann, 1932, 352 p 18. . Лаврентьев М.М. О некоторых некорректных задачах математической физики. – Новосибирск: Изд-во Сиб. отделения АН СССР, 1962, 68 с. 19. Лаврентьев М.М. Романов В.Г., Шишатский С.П. Некорректные задачи математической физики и анализа.– М.: Наука. 1980, 288 с. 20. Федотов А.М. Некорректные задачи со случайными ошибками в данных.– Новосибирск, Наука, 1982, 280 с. 21. Краснов М.Л. Интегральные уравнения.– М.: Наука. 1975. 22. Воробьев Ю.В. Метод моментов в прикладной математике.– М.: Физматгиз, 1958. 23. Раутиан С.Г. Реальные спектральные приборы.– УФН, 1958, т.66, вып.3,с.475. 24. Линник Ю.В. Метод наименьших квадратов и основы теории обработки наблюдений.– М.: Физматгиз. 1958. 25. Фаддеева В.Н., Фаддеев Д.К. Вычислительные методы линейной алгебры.– М.: Физматгиз. 1960. 26. Марчук Г.И., Кузнецов Ю.А. Итерационные методы и квадратичные функционалы.– В кн.: Методы вычислительной математики.– Новосибирск: Наука. 1975. 27. Тихонов А.Н. Об устойчивости обратных задач.–ДАН СССР, 1962, т.39, вып.5 28. .Марчук Г.И. О постановке некоторых обратных задач.–ДАН СССР, 1964, т.156, вып.3. 29. Лаврентьев М.М. Об интегральных уравнениях первого рода.–ДАН СССР, 1959, т.127, вып.1. 30. Иванов В.К. О линейных некорректных задачах.–ДАН СССР, 1962, т.145, вып.2. 31. Phillips D.L. A technique for the numerical solution of certain integral equations of the first kind.–J. Assoc. Comp. Mash. , 1962, v.9, №1. 32. Латтес Р., Лионс Ж.Л. Метод квазиобращения и его приложения: Пер. с англ.– М: Мир, 1970. 33. Жуковский Е.Л. Статистическая регуляризация алгебраических систем уравнений.– ЖМФ и МФ, 1972, т.12, вып.1. 34. Лаврентьев М.М., Васильев В.Г. О постановке некорректных задач математической физики.– Сиб. матем. журн., 1966, т.7, вып.3. 35. Тихонов А.Н. О решении некорректно поставленных задач.–ДАН СССР, 1963, т.153, вып.3. 36. Рао С.Р. Линейные статистические методы и их приложения: Пер. с англ.– М.: Наука, 1968. 37. Канторович Л.В.– Сиб. матем. журн., 1962, т.3, вып.5. – с.701. 38. Преображенский Н.Г., Пикалов В.В. Неустойчивые задачи диагностики плазмы.– Новосибирск: Наука, 1982, 236 с. 39. Salakhov M.Kh.– Spectrochim. Acta Rev, 1993, v.5, №6, p.399. 40. Морозов В.А. Линейные и нелинейные некорректные задачи.– Итоги науки и техники: Математический анализ/ВИНИТИ.– 1973. Содержание Стр. Введение………………………………………………………………….4 Глава 1. Основы работы с системой MATLAB…...………………………8 Глава 2. Задачи восстановления сигналов……………………………….24 Глава 3. Обработка экспериментальных данных методом опорных векторов с составным шагом………………………………...……………54 Глава 4. Интерполяция и аппроксимация данных… ………………….75 Глава 5. Определение параметров составляющих сложного сигнала….83 Литература…………………………………………………………………93
Приложение. Некоторые функции и операторы MATLAB.
· image(Z) – возвращает мнимые части элементов массива Z. · real(Z) – возвращает вещественные части элементов комплексного массива Z. · conj(Z) – возвращает число, комплексно-сопряженное аргументу Z. · linespace(a,b,n) – генерирует n точек, равномерно распределенный в интервале от a до b. linespace(a,b) – возвращает линейный массив из 100 точек, равномерно распределенных в интервале от a до b. · D=size(a) – для mxn матрицы A возвращает двухэлементный вектор-строку, в котором первая составляющая– число строк m, а вторая составляющая – число столбцов n. [m,n]=size(A) возвращает число рядов и столбцов в разных выходных параметрах m и n. · rand – генерирует массивы случайных чисел, значения элементов которых равномерно распределены в промежутке (0,1). rand(n) – возвращает матрицу размера nxn. rand(n,m) – возвращает матрицу размера mxn. rand(size(A)) – возвращает массив того же размера, что и A, с элементами, распределенными по равномерному закону. · X=diag(v) –помещает вектор v на главную диагональ.V=diag(X) – возвращает главную диагональ матрицы X. · det(X) – возвращает определитель квадратной матрицы X. · rank(A) – возвращает количество сингулярных чисел, которые являются большими, чем заданный по умолчанию допуск. · norm(X,p) , где p– целое положительное число, – возвращает корень степени p из суммы абсолютных значений элементов вектора X, возведенный в степень p. · inv(X) – возвращает матрицу, обратную квадратной матрице X.Выдается предупреждающее сообщение, если X плохо масштабирована или близка к вырожденной. B=pinv(A) возвращает матрицу, псевдообратную матрице А. · fft(X) – возвращает для вектора X дискретное преобразование Фурье, по возможности используя алгоритм быстрого преобразование Фурье. Если X – матрица, функция fft возвращает преобразование Фурье для каждого столбца матрицы. Ifft(F) – возвращает результат дискретного обратного преобразования Фурье вектора F. · max(A) – возвращает наибольший элемент, если A– вектор; или возвращает вектор-строку, содержащую максимальные элементы каждого столбца, если А– матрица. · min (A) – возвращает наименьший элемент, если A– вектор; или возвращает вектор-строку, содержащую минимальные элементы каждого столбца, если А– матрица. · mean(A) – возвращает арифметическое среднее значение элементов массива, если A – вектор или вектор – строку, содержащую средние значения каждого столбца, если А – матрица. · sort(A) – в случае одномерного массива А сортирует и возвращает элементы по возрастанию их значений; в случае двумерного массива происходит сортировка и возврат элементов каждого столбца. Допустимы вещественные, комплексные и строковые элементы. Если А принимает комплексные значения, то элементы сначала сортируются по абсолютному значению, а затем, если абсолютные значения равны, по аргументу. · plot(X,Y) – строит график функции y(x), координаты точек (x,y) которой берутся из векторов одинакового размера X,Y. Если X или Y – матрица, то строится семейство графиков по данным, содержащимся в колонках матрицы. · [B,d]=spdiags(A) – извлекает все ненулевые диагонали из матрицы A размера mxn. B– матрица размера min(m,n)xp, столбцы которой p являются ненулевыми диагоналями A. d – вектор длины p, целочисленные элементы которого точно определяют номера диагоналей матрицы A (положительные номера – выше главной диагонали, отрицательные – ниже). · nnz(X) – возвращает число ненулевых элементов матрицы X. · lsqr(A,B) – возвращает точное Решение X системы линейных уравнений A*X=B, если матрица хорошо обусловленная. В противном случае – возвращает решение, полученное итерационным методом наименьших квадратов. Матрица коэффициентов A должна быть прямоугольной размера mxn , а вектор-столбец правых частей уравнений B должен иметь размер m. Условие m³n может быть и необязательным. Функция lsq начинает итерации от начальной оценки, по умолчанию представляющий собой вектор размером n, состоящий из нулей. Итерации производятся или до сходимости к решению, или до появления ошибки, или до достижения максимального числа итераций (по умолчанию равного min(20,m,n). Сходимость достигается, когда отношение вторых норм векторов norm(B-Ax)/norm(B) меньше или равно погрешности метода tol(по умолчанию 10-6). · A(:,j) – j-ый столбец из матрицы A. · A(i,:j) – j-ая строка из матрицы A. · A(j:k) – это A(j), A(j+1),…A(k). · A(:,j:k) – это A(:,j), A(:,j+1),…A:,(k). · A(:) – записывает все элементы массива A в виде столбца. · A(m,:) – удаляет строку m из матрицы A. · A(:,n) – удаляет столбец n из матрицы A. · /– правое деление. Выражение X=B/A дает решение систем линейных уравнений AX=B, где A – матрица размером mxn и B – матрица размера nxk ; · \ – левое деление. Выражение X=B\A дает решение систем линейных уравнений AX=B, где A – матрица размером mxn и B – матрица размера nxk.

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|

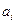 ,
, 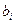 ,
, 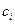 – параметры элементарных составляющих сложного сигнала, подлежащие определению, m – количество исходных составляющих. Умножив обе части на множитель:
– параметры элементарных составляющих сложного сигнала, подлежащие определению, m – количество исходных составляющих. Умножив обе части на множитель:
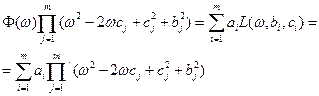
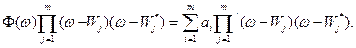
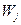 ,
,  , входящие в (5.4), определяются из уравнения
, входящие в (5.4), определяются из уравнения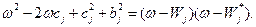
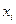 ,
, 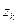 (i=1,2,….,2m), (k=1,2,…,2m-1), которые определяются равенствами.
(i=1,2,….,2m), (k=1,2,…,2m-1), которые определяются равенствами.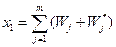
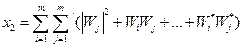
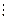
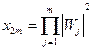
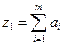
 (5.7)
(5.7)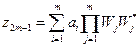
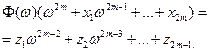
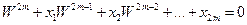
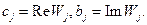


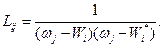
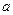 – амплитуда модельной функции,
– амплитуда модельной функции, 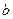 – положение центра,
– положение центра, 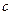 – полуширина,
– полуширина, 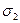 модельного сигнала от восстановленного по вновь найденным параметрам определяется в виде:
модельного сигнала от восстановленного по вновь найденным параметрам определяется в виде: ,
, – истинный суммарный контур,
– истинный суммарный контур,  – вычисленный по наблюденным параметрам суммарный контур.
– вычисленный по наблюденным параметрам суммарный контур.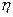 =8% решение становится бессмысленным: a1=0,58 (при заданном равном 1), a2=2,98(2), b1=0(1), b2=2,46(2), c1=1,5(3), c2=9,99(9). В то время как после применения метода статистической регуляризации параметры вычисляются уже намного лучше, так становятся a1=0,86, a2=2,47, b1=0,77, b2=2,2, c1=3,1, c2=9,27(значения параметров задаются в единицах полуширины первого контура). Итак, получаем, что использование методов статистической регуляризации позволяет значительно увеличить точность решения.
=8% решение становится бессмысленным: a1=0,58 (при заданном равном 1), a2=2,98(2), b1=0(1), b2=2,46(2), c1=1,5(3), c2=9,99(9). В то время как после применения метода статистической регуляризации параметры вычисляются уже намного лучше, так становятся a1=0,86, a2=2,47, b1=0,77, b2=2,2, c1=3,1, c2=9,27(значения параметров задаются в единицах полуширины первого контура). Итак, получаем, что использование методов статистической регуляризации позволяет значительно увеличить точность решения.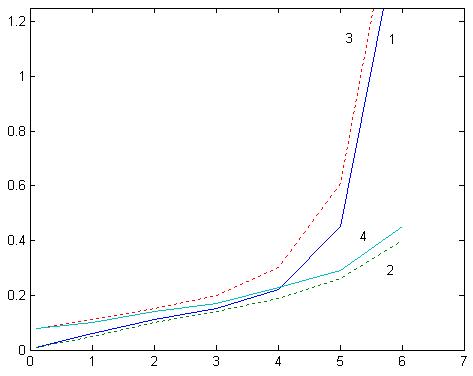
 .
. мы поставили
мы поставили 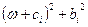 ) дает неудовлетворительные результаты даже при таком небольшом уровне ошибок.
) дает неудовлетворительные результаты даже при таком небольшом уровне ошибок.