|
Метод регуляризации А.Н.Тихонова
Стремление избавиться от произвольных факторов и определить общие методы решения некорректных задач привело к разработке новых подходов к их решению [27-34]. Фундаментальное значение для новых подходов имеют понятия регуляризации решения и регуляризирующего оператора, введенные А. Н. Тихоновым [4].
Под регуляризацией решения по Тихонову понимается построение семейства обратных операторов, зависящего от некоторого числового параметра  , называемого параметром регуляризации. Каждый оператор семейства дает решение корректной задачи, причем при согласованном стремлении к нулю параметра , называемого параметром регуляризации. Каждый оператор семейства дает решение корректной задачи, причем при согласованном стремлении к нулю параметра  и ошибки исходных данных решение корректной задачи стремится к истинному решению соответствующей некорректной задачи. и ошибки исходных данных решение корректной задачи стремится к истинному решению соответствующей некорректной задачи.
Иначе говоря, если в некорректной задаче K  = f вместо точной правой части = f вместо точной правой части  мы имеем элемент мы имеем элемент  , для которого , для которого  ( (  – погрешность исходных данных – погрешность исходных данных  ), то элемент ), то элемент  по Тихонову можно определить с помощью оператора, зависящего от параметра по Тихонову можно определить с помощью оператора, зависящего от параметра  , значения которого надо брать согласованными с погрешностью исходных данных , значения которого надо брать согласованными с погрешностью исходных данных  . Эта согласованность должна быть такой, чтобы при приближении правой части . Эта согласованность должна быть такой, чтобы при приближении правой части  к точному значению к точному значению  , т.е. при , т.е. при  , приближенное решение , приближенное решение  стремилось бы к точному решению стремилось бы к точному решению  (а метрике пространства Φ). (а метрике пространства Φ).
Оператор  , зависящий от параметра , зависящий от параметра  , называется регуляризирующим для уравнения K , называется регуляризирующим для уравнения K  = f, если он обладает следующими свойствами: = f, если он обладает следующими свойствами:
оператор определен для всякого  и любого и любого  и непрерывен по f ; и непрерывен по f ;
существует такая функция от  , ,  , и для любого , и для любого  существует такое число существует такое число  , что если , что если  , то , то  , где , где 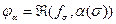 . .
Задача получения приближенного решения уравнения K  = f, устойчивого к малым изменениям правой части, в методе регуляризации А.Н.Тихонова сводится, во-первых, к нахождению регуляризирующих операторов и, во-вторых, к определению параметра регуляризации = f, устойчивого к малым изменениям правой части, в методе регуляризации А.Н.Тихонова сводится, во-первых, к нахождению регуляризирующих операторов и, во-вторых, к определению параметра регуляризации  по дополнительной информации о задаче. Строго говоря, регуляризация подменяет исходную задачу другой. Нужно, чтобы регуляризация, не меняя физического содержания задачи, только избавляла нас от ее вычислительной неустойчивости. Другими словами, введение априорной информации позволяет значительно сузить область допустимых решений. Разным видам априорной информации соответствуют разные способы регуляризации. по дополнительной информации о задаче. Строго говоря, регуляризация подменяет исходную задачу другой. Нужно, чтобы регуляризация, не меняя физического содержания задачи, только избавляла нас от ее вычислительной неустойчивости. Другими словами, введение априорной информации позволяет значительно сузить область допустимых решений. Разным видам априорной информации соответствуют разные способы регуляризации.
Главной особенностью метода регуляризации А.Н.Тихонова, отличающей его от других общих методов решения некорректно поставленных задач [29, 30, 32], является его применимость в ситуации, когда класс Φ возможных решений уравнения K  =f не является компактом. Эта ситуация как раз характерна для задач восстановления сигналов, в которых обратный оператор основного уравнения заведомо не является непрерывным. =f не является компактом. Эта ситуация как раз характерна для задач восстановления сигналов, в которых обратный оператор основного уравнения заведомо не является непрерывным.
Способ построения регуляризирующих операторов в методе А.Н.Тихонова основан на вариационном принципе и состоит в следующем [35]. Пусть  – некоторый неотрицательный функционал, определенный на подмножестве Φ1 множества Φ и такой, что для всякого числа – некоторый неотрицательный функционал, определенный на подмножестве Φ1 множества Φ и такой, что для всякого числа  множество Φ1,с элементов множество Φ1,с элементов  из Φ1, для которых из Φ1, для которых  , является компактом на Φ1. Функционалы , является компактом на Φ1. Функционалы  , обладающие такими свойствами, называются стабилизирующими функционалами. Вполне понятно, что выбор функционала , обладающие такими свойствами, называются стабилизирующими функционалами. Вполне понятно, что выбор функционала  неоднозначен. неоднозначен.
Пусть далее известно, что 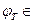 Φ1 и уклонение правой части Φ1 и уклонение правой части  от точного значения от точного значения  не превосходит не превосходит  , т.е. , т.е.  (K (K  , ,  ) )  . Тогда приближенное решение естественно искать в классе . Тогда приближенное решение естественно искать в классе  элементов элементов  , для которых , для которых  (K (K  , ,  ) )  . Но класс . Но класс  возможных решений слишком широкий. Его надо сузить, используя какой-то способ отбора возможных решений, обеспечивающий получение в качестве приближенного решения такого элемента (или элементов) из возможных решений слишком широкий. Его надо сузить, используя какой-то способ отбора возможных решений, обеспечивающий получение в качестве приближенного решения такого элемента (или элементов) из  , который непрерывно зависел бы от , который непрерывно зависел бы от  . В качестве такого принципа и берется вариационный принцип. . В качестве такого принципа и берется вариационный принцип.
С целью сужения класса возможных решений рассматриваются только такие элементы множества  , на которых определен заданный функционал , на которых определен заданный функционал  , т.е. рассматриваются лишь элементы, принадлежащие множеству , т.е. рассматриваются лишь элементы, принадлежащие множеству  . Среди элементов этого множества находят такой (такие), который минимизирует функционал . Среди элементов этого множества находят такой (такие), который минимизирует функционал  . Нахождение такого элемента – задача на условный экстремум. Решение ее методом неопределенных множителей Лагранжа сводится к поиску минимума функционала . Нахождение такого элемента – задача на условный экстремум. Решение ее методом неопределенных множителей Лагранжа сводится к поиску минимума функционала
 (K (K  , ,  )+ )+   , (2.21) , (2.21)
где числовой параметр  определяется из условия определяется из условия  (K (K  , ,  ) )  , в котором , в котором  – элемент, на котором функционал (4.1) достигает минимума. Функционал – элемент, на котором функционал (4.1) достигает минимума. Функционал 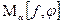 также называется функционалом Тихонова. также называется функционалом Тихонова.
Элемент  можно рассматривать как результат применения к правой части можно рассматривать как результат применения к правой части  исходного уравнения некоторого оператора исходного уравнения некоторого оператора  , зависящего от параметра , зависящего от параметра  , т.е. , т.е.  . Доказано [4], что оператор . Доказано [4], что оператор  является регуляризирующим и, следовательно, в качестве приближенного решения уравнения K является регуляризирующим и, следовательно, в качестве приближенного решения уравнения K  =f с правой частью =f с правой частью  можно взять элемент можно взять элемент  . .
Таким образом, в качестве приближенного решения исходной задачи берется решение другой задачи (задачи на минимум функционала 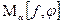 ), близкой к исходной при малых значениях погрешности задания правой части ), близкой к исходной при малых значениях погрешности задания правой части  . В то время как исходная задача не обладает устойчивостью к малым изменениям «входных данных» . В то время как исходная задача не обладает устойчивостью к малым изменениям «входных данных»  , задача минимизации функционала , задача минимизации функционала 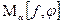 обладает этим свойством. Устойчивость достигнута сужением класса возможных решений с помощью введения в рассмотрение функционала обладает этим свойством. Устойчивость достигнута сужением класса возможных решений с помощью введения в рассмотрение функционала  , играющего стабилизирующую роль. Поэтому функционалы , играющего стабилизирующую роль. Поэтому функционалы  называют стабилизаторами задачи. называют стабилизаторами задачи.
В качестве стабилизатора можно взять
 , (2.22) , (2.22)
где 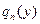 – заданные неотрицательные функции. – заданные неотрицательные функции.
Функционалы вида (2.22) называются стабилизаторами p-го порядка. Функционалы этого вида по существу характеризуют «гладкость» функции  . Следовательно, используя их при поиске минимума выражения (1.4.1), мы стремимся выбрать из множества функций . Следовательно, используя их при поиске минимума выражения (1.4.1), мы стремимся выбрать из множества функций  , удовлетворяющих условию , удовлетворяющих условию  (K (K  , ,  ) )  , некоторую «самую гладкую» функцию , некоторую «самую гладкую» функцию  (во всяком случае, более гладкую, чем решение без регуляризации). Различным критериям гладкости, позволяющим сравнивать функции (во всяком случае, более гладкую, чем решение без регуляризации). Различным критериям гладкости, позволяющим сравнивать функции  рассматриваемого множества, отвечают различные функционалы (2.22), образуемые при различных p. Степень «сглаживания» решения регулируется параметром рассматриваемого множества, отвечают различные функционалы (2.22), образуемые при различных p. Степень «сглаживания» решения регулируется параметром  . .
Перейдем теперь к применению метода регуляризации для решения основного интегрального уравнения :
 , ,
полагая, что восстанавливаемый сигнал непрерывен на  , а , а 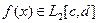 . Воспользуемся для простоты выкладок стабилизатором 1-го порядка . Воспользуемся для простоты выкладок стабилизатором 1-го порядка
 . .
Тогда регуляризованное решение 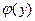 должно минимизировать функционал должно минимизировать функционал
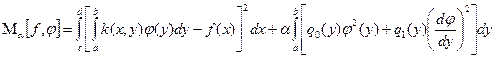 . (2.23) . (2.23)
При использовании матричной формы записи уравнений регуляризованное решение удается получить в явном виде. Функционал (2.23) можно записать в следующем виде:
 (К (К  - -  )Т(К )Т(К  - -  )+ )+  Т( Т(   + +  ) )  (2.24) (2.24)
где  и и  – векторы, полученные дискретизацией наблюдаемой функции – векторы, полученные дискретизацией наблюдаемой функции  и восстанавливаемого сигнала и восстанавливаемого сигнала 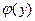 на сетках с шагом на сетках с шагом  и и  соответственно; К – матрица отсчетов соответственно; К – матрица отсчетов 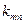 весовой функции весовой функции  в опорных точках; I – единичная матрица; в опорных точках; I – единичная матрица;  – ленточная квадратная матрица, – ленточная квадратная матрица,  , где матрица , где матрица  – матрица численного дифференцирования [6, с.95] – матрица численного дифференцирования [6, с.95]
 (2.25) (2.25)
«производная вперед», или [5, с.22] «производная назад»:
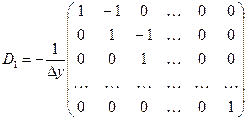
Для того, чтобы найти вектор  , минимизирующий функционал (2.24), вычислим градиент этого функционала по , минимизирующий функционал (2.24), вычислим градиент этого функционала по  , пользуясь следующими формулами векторного дифференцирования [36]: , пользуясь следующими формулами векторного дифференцирования [36]:
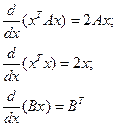
Приравняем градиент нулю, положим  = =  =1 и получим выражение для =1 и получим выражение для  . Таким образом найдем регуляризованное решение в явном виде: . Таким образом найдем регуляризованное решение в явном виде:
 . (2.26) . (2.26)
Это решение отвечает случаю применения тихоновских стабилизаторов 1-го порядка. Как это следует из (2.26), точность решения  зависит от параметра регуляризации зависит от параметра регуляризации  . Поэтому ясно, что процедура определения этого параметра является центральной в регуляризирующих схемах получения приближенных решений. . Поэтому ясно, что процедура определения этого параметра является центральной в регуляризирующих схемах получения приближенных решений.
Существует много способов выбора параметра  , позволяющего заметно улучшить сходимость регуляризованного решения , позволяющего заметно улучшить сходимость регуляризованного решения  к истинному решению к истинному решению  . Одним из наиболее эффективных и хорошо изученных методов является метод невязки, предложенный Филлипсом [31] и Канторовичем [37]. Практически все методы, определяющие . Одним из наиболее эффективных и хорошо изученных методов является метод невязки, предложенный Филлипсом [31] и Канторовичем [37]. Практически все методы, определяющие  , в том числе [3,38,39] и все они зависят от той информации, которая имеется относительно приближенных входных данных, например, если известен шум в исходных данных , в том числе [3,38,39] и все они зависят от той информации, которая имеется относительно приближенных входных данных, например, если известен шум в исходных данных  ( ( 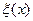 – случайный стационарный процесс с нулевым средним: – случайный стационарный процесс с нулевым средним:  , и ковариационной матрицей , и ковариационной матрицей 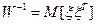 ), то параметр регуляризации ), то параметр регуляризации  при допонительном условии, что оператор при допонительном условии, что оператор  является регуляризирующим, можно определить по невязке является регуляризирующим, можно определить по невязке  (K (K  , ,  ) )  . На практике это делается методом проб и ошибок. Например, если мы знаем приближенное значение е функционала . На практике это делается методом проб и ошибок. Например, если мы знаем приближенное значение е функционала  , характеризующего степень гладкости восстанавливаемого сигнала (формула (1.4.2) при р=0), то хорошей оценкой , характеризующего степень гладкости восстанавливаемого сигнала (формула (1.4.2) при р=0), то хорошей оценкой  служит величина, обратная е [40]. Эффективность того или иного способа определения величины служит величина, обратная е [40]. Эффективность того или иного способа определения величины  обычно устанавливается с помощью вычислительного эксперимента. обычно устанавливается с помощью вычислительного эксперимента.
Метод регуляризации А.Н.Тихонова требует минимума априорной информации о задаче. Практически используется лишь информация о характере гладкости решения и о том, что восстанавливаемая функция задана на отрезке  . Дополнительная информация, если она имеется, может быть использована для определения конкретного значения параметра регуляризации . Дополнительная информация, если она имеется, может быть использована для определения конкретного значения параметра регуляризации  . .
Метод регуляризации А.Н.Тихонова хорошо зарекомендовал себя при решении самых разных некорректных задач, в том числе и задач восстановления сигналов.
Не нашли, что искали? Воспользуйтесь поиском по сайту:
©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|


 , называемого параметром регуляризации. Каждый оператор семейства дает решение корректной задачи, причем при согласованном стремлении к нулю параметра
, называемого параметром регуляризации. Каждый оператор семейства дает решение корректной задачи, причем при согласованном стремлении к нулю параметра  = f вместо точной правой части
= f вместо точной правой части  мы имеем элемент
мы имеем элемент  , для которого
, для которого  (
(  – погрешность исходных данных
– погрешность исходных данных  ), то элемент
), то элемент  по Тихонову можно определить с помощью оператора, зависящего от параметра
по Тихонову можно определить с помощью оператора, зависящего от параметра  , приближенное решение
, приближенное решение  стремилось бы к точному решению
стремилось бы к точному решению  (а метрике пространства Φ).
(а метрике пространства Φ). , зависящий от параметра
, зависящий от параметра  и любого
и любого  и непрерывен по f ;
и непрерывен по f ; , и для любого
, и для любого  существует такое число
существует такое число  , что если
, что если  , то
, то  , где
, где 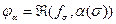 .
. – некоторый неотрицательный функционал, определенный на подмножестве Φ1 множества Φ и такой, что для всякого числа
– некоторый неотрицательный функционал, определенный на подмножестве Φ1 множества Φ и такой, что для всякого числа  множество Φ1,с элементов
множество Φ1,с элементов  , является компактом на Φ1. Функционалы
, является компактом на Φ1. Функционалы 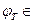 Φ1 и уклонение правой части
Φ1 и уклонение правой части  (K
(K  . Тогда приближенное решение естественно искать в классе
. Тогда приближенное решение естественно искать в классе  элементов
элементов  . Среди элементов этого множества находят такой (такие), который минимизирует функционал
. Среди элементов этого множества находят такой (такие), который минимизирует функционал  (K
(K  ,
,  , в котором
, в котором 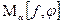 также называется функционалом Тихонова.
также называется функционалом Тихонова. , зависящего от параметра
, зависящего от параметра  . Доказано [4], что оператор
. Доказано [4], что оператор  можно взять элемент
можно взять элемент  , задача минимизации функционала
, задача минимизации функционала  , (2.22)
, (2.22)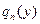 – заданные неотрицательные функции.
– заданные неотрицательные функции. ,
, , а
, а 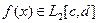 . Воспользуемся для простоты выкладок стабилизатором 1-го порядка
. Воспользуемся для простоты выкладок стабилизатором 1-го порядка .
.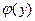 должно минимизировать функционал
должно минимизировать функционал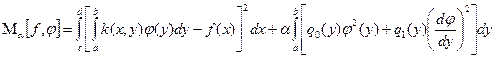 . (2.23)
. (2.23) (К
(К  Т(
Т( 
 +
+  )
)  и восстанавливаемого сигнала
и восстанавливаемого сигнала  и
и  соответственно; К – матрица отсчетов
соответственно; К – матрица отсчетов 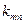 весовой функции
весовой функции  в опорных точках; I – единичная матрица;
в опорных точках; I – единичная матрица;  , где матрица
, где матрица  – матрица численного дифференцирования [6, с.95]
– матрица численного дифференцирования [6, с.95] (2.25)
(2.25)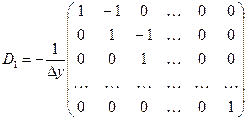
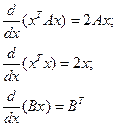
 . (2.26)
. (2.26) (
( 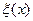 – случайный стационарный процесс с нулевым средним:
– случайный стационарный процесс с нулевым средним:  , и ковариационной матрицей
, и ковариационной матрицей 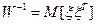 ), то параметр регуляризации
), то параметр регуляризации  является регуляризирующим, можно определить по невязке
является регуляризирующим, можно определить по невязке