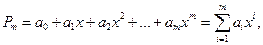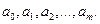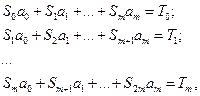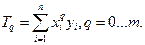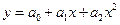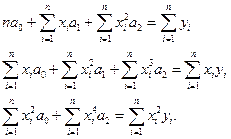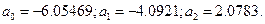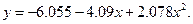Глава 4. Интерполяция и аппроксимация данных.

Под аппроксимацией обычно подразумевается описание некоторой, порой не заданной явно зависимости, или совокупности представляющих ее данных с помощью другой, обычно более простой или более единообразной зависимости. Часто данные находятся в виде отдельных узловых точек, координаты которых задаются таблицей данных.

Результат аппроксимации может не проходить через узловые точки. Напротив, задача интерполяции – найти данные в окрестностях узловых точек. Для этого используют подходящие функции, значения которых в узловых точках совпадают с координатами этих точек. Например, при линейной интерполяции зависимости y(x) узловые точки соединяются друг с другом отрезками прямых, и считается, что искомые промежуточные точки расположены на этих отрезках.

Для повышения точности интерполяции применяют параболы (квадратичная интерполяция) или полиномы более высокой степени (полиномиальная интерполяция). Для обработки данных MATLAB использует различные функции интерполяции и аппроксимации данных. В этой главе мы рассмотрим алгоритм аппроксимации функции методом наименьших квадратов (МНК), а также опишем набор собственных функций MATLAB, реализующих методы аппроксимации и интерполяции. Предположим, что в результате исследования некоторой величины получены значения для функции f(x) в точках x_i (i=1,…n):

Y₁=f(x₁), Y₂=f(x₂),…., Y_n=f(x_n).

Требуется описать эту функцию многочленом степени m (m<n)

таким образом, чтобы значение функции

(4.1)

было минимальным за счет соответствующего выбора коэффициентов многочлена

Функция (4.1) является неотрицательной квадратичной формой, которая имеет минимум. Необходимые условия минимума этой функции образуют систему из m+1 линейных уравнений с m+1 неизвестными:

(4.2)

Перепишем систему (4.2) в виде:

(4.3)

где

Степень m подбираемого многочлена может быть определена графически или методом конечных разностей. Если значения аргумента x={x_i} произвольны, то в координатной плоскости строятся точки {x_i,y_i} и проводится плавная линия как можно ближе к ломаной, соединяющей эти точки. Вид полученной кривой сравнивается с графиками известных элементарных функций. Если значения x={x_i} , то степень полинома P_m , то степень полинома P_m определяется порядком конечных разностей: постоянство разностей k-го порядка указывает, что степень полинома m=k. Зная степень аппроксимирующего полинома, его уравнение можно найти, воспользовавшись МНК. Для проверки полученного уравнения на адекватность можно использовать заранее заданную относительную погрешность функции.

Пример расчета. Подберем вид функции, аппроксимирующей исходные данные, приведенные в Табл.1.

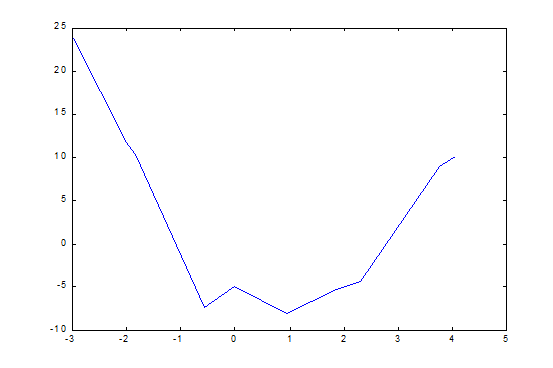
Определим вид зависимости. Так как значения аргумента произвольны, сделаем это с помощью графика.

Рис.5.Определение вида кривой.

По виду кривой предположим, что данная функция может быть аппроксимирована формулой:

При m=2 система уравнений (4.3) примет вид:

(4.4)

Вычислим коэффициенты системы (Табл. 2).

Подставим полученные значения в (4.4) и система уравнений примет вид:

(4.5)

Решение системы (4.4)

Построенное уравнение имеет вид:

Относительная погрешность аппроксимации 23.5%.

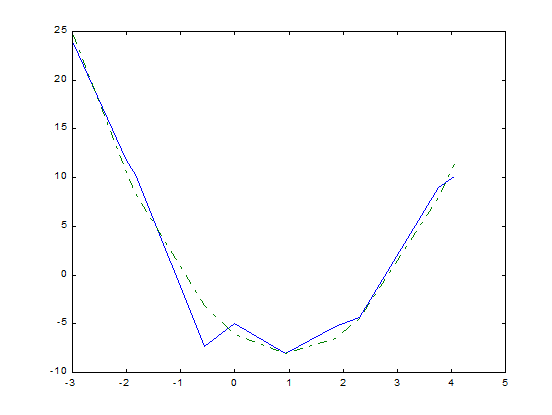
Рис.6. Сплошная кривая построена по экспериментальным данным, штрих пунктирная кривая построена с помощью найденного аппроксимирующего полинома.

В системе MATLAB определены функции аппроксимации данных полиномов по методу наименьших квадратов – полиномиальная регрессия. Функция polyfit(x.y.n) – возвращает вектор коэффициентов полинома p(x) cтепени n, который с наименьшей среднеквадратичной погрешностью аппроксимирует функцию y(x). Результатом является вектор-строка длиной n+1 , содержащий коэффициенты полинома в порядке уменьшения степени x. Ниже приведен пример использования функции полиномиальной регрессии для рассмотренных ранее массивов данных.

» x=[-2.98 -2.01 -1.83 -0.56 0 0.94 1.85 2.31 3.76 4.05];

» y=[23.76 11.72 10.34 -7.34 -5 -8.01 -5.31 -4.31 9.001 10.11];

» g=polyfit(x,y,2)

g =

2.0743 -4.0885 -6.0176

» z=g(3)+g(2)*x+g(1)*x.*x

z =

Columns 1 through 7

24.5864 10.5805 8.4108 -3.0776 -6.0176 -8.0280 -6.4821

Columns 8 through 10

-4.3935 7.9349 11.4472

Сплайн-интерполяция используется для представления данных отрезками полиномов невысокой степени – чаще всего третьей. При этом кубическая интерполяция обеспечивает непрерывность первой и второй производных результата интерполяции в узловых точках. Из этого вытекают следующие свойства сплайн-интерполяции:

· график кусочно-полиномиальной аппроксимирующей функции проходит точно через узловые точки;

· в узловых точках нет разрывов и резких перегибов функции;

· поскольку используется множество полиномов, появляется возможность аппроксимировать функции с множеством пиков и впадин.

График интерполирующей функции при этом виде интерполяции можно уподобить кривой, по которой изгибается гибкая линейка, закрепленная в узловых точках. В переводе spline означает “гибкая линейка”. Реализуется сплайн-интерполяция следующей функцией:

yi=spline(x,y,xi) –использует векторы x и y, содержащие аргументы функции и ее значения, и вектор xi, задающий новые точки; для нахождения элементов вектора yi используется кубическая сплайн-интерполяция.

Пример:

» x=0:10;y=3*cos(x);

» x1=0:0.1:11;

» y1=spline(x,y,x1);

» plot(x,y,'o',x1,y1,'--')

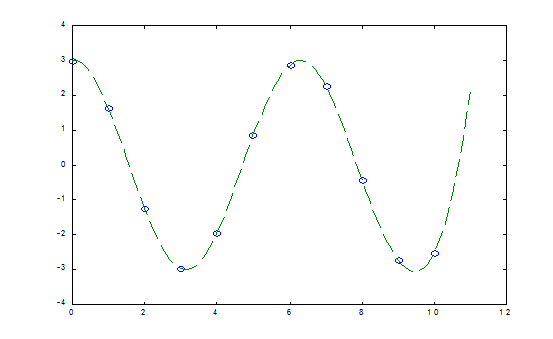
Рис.7. Пример применения функции spline.

Ввиду важности сплайн-интерполяции и аппроксимации в обработке и представлении сложных данных в состав системы MATLAB входит пакет Spline Toolbox, содержащий около 70 дополнительных функций, относящихся к реализации сплайн-интерполяции и аппроксимации. Для вызова данных об этом пакете (если он установлен) используется команда help splines.

Не нашли, что искали? Воспользуйтесь поиском по сайту: