Некорректность задачи восстановления сигналов
Проверим три необходимых для корректности задачи условия [4].
1. Существование решения. Вопрос о существовании решения интегрального уравнения
 (2.14) (2.14)
тесно связан с условиями, налагаемыми на ядро  и на правую часть и на правую часть  .решение может не существовать вообще, либо существовать не для всякой правой части. Например, если ядро имеет непрерывную производную по х, то и правая часть уравнения также должна иметь непрерывную производную по х. Если же правая часть содержит точки, в которых функция .решение может не существовать вообще, либо существовать не для всякой правой части. Например, если ядро имеет непрерывную производную по х, то и правая часть уравнения также должна иметь непрерывную производную по х. Если же правая часть содержит точки, в которых функция  не имеет производной (этот случай встречается, например, когда воспроизводимый график не имеет производной (этот случай встречается, например, когда воспроизводимый график  оказывается ломаной линией), то очевидно, что при наличии ядра с непрерывной производной уравнение (2.14) не имеет решения. Таким образом, существование решения зависит от того, к каким классам (пространствам) функций Φ и F по сути задачи относятся сигнал оказывается ломаной линией), то очевидно, что при наличии ядра с непрерывной производной уравнение (2.14) не имеет решения. Таким образом, существование решения зависит от того, к каким классам (пространствам) функций Φ и F по сути задачи относятся сигнал 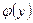 и отклик и отклик  . Естественно, уравнение (2.14) имеет решение только для таких правых частей . Естественно, уравнение (2.14) имеет решение только для таких правых частей  , которые принадлежат образу KΦ множества Φ функций , которые принадлежат образу KΦ множества Φ функций 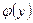 при отображении при отображении
f=K  Φ. Φ.
Пусть ядро уравнения (2.14) является симметричным ядром:
 . .
Тогда в силу теоремы Гильберта-Шмидта [20] для существования решения уравнения (2.14) необходимо, чтобы функция  разлагалась по собственным функциям разлагалась по собственным функциям 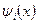 ядра ядра  : :
 . .
Здесь 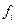 – коэффициенты разложения функции – коэффициенты разложения функции  относительно собственных функций ядра: относительно собственных функций ядра:
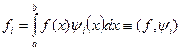 , ,
а собственные функции 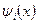 удовлетворяют интегральным уравнениям вида удовлетворяют интегральным уравнениям вида
 , ,
где 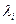 – собственные значения (собственные числа) ядра – собственные значения (собственные числа) ядра  . Заметим, что симметричность ядра гарантирует существование собственных значений и их действительность, а также ортогональность собственных функций, отвечающих различным собственным значениям. . Заметим, что симметричность ядра гарантирует существование собственных значений и их действительность, а также ортогональность собственных функций, отвечающих различным собственным значениям.
Если система собственных функций симметричного ядра  является полной, причем, является полной, причем,   и и   (предполагается, что (предполагается, что  , , 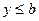 ), то уравнение (2.14) имеет решение, принадлежащее ), то уравнение (2.14) имеет решение, принадлежащее  , и притом единственное, тогда и только тогда, когда ряд , и притом единственное, тогда и только тогда, когда ряд
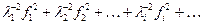 (2.15) (2.15)
сходится. Это утверждение составляет содержание теоремы Пикара [21].
Если отказаться от предположения о симметричности ядра и принадлежности его к  и считать, что и считать, что  – просто некоторое непрерывное ядро, то можно показать, сто уравнение (2.14) может не иметь решения и в классе – просто некоторое непрерывное ядро, то можно показать, сто уравнение (2.14) может не иметь решения и в классе  . Например, если ядро . Например, если ядро  является многочленом по переменной х является многочленом по переменной х
 , (2.16) , (2.16)
То левая часть уравнения (2.14) будет иметь вид
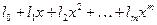
и, следовательно, такой же вид должна иметь и правая часть (2.14), т.е. функция  . В частности, если ядро уравнения (2.14) равно . В частности, если ядро уравнения (2.14) равно  , то уравнение имеет решение только для таких правых частей , то уравнение имеет решение только для таких правых частей  , которые являются линейной функцией х. Отсюда следует, что если функция , которые являются линейной функцией х. Отсюда следует, что если функция  – произвольная непрерывная на – произвольная непрерывная на  , то при данном ядре (2.16) уравнение (2.14) не имеет решения. , то при данном ядре (2.16) уравнение (2.14) не имеет решения.
В практических задачах восстановления сигналов мы обычно уверены в существовании функции 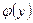 , стоящей под интегралом в левой части уравнения (2.14). Отсутствие решения в таких задачах может объясняться лишь неадекватностью математической модели реальному функционированию системы. , стоящей под интегралом в левой части уравнения (2.14). Отсутствие решения в таких задачах может объясняться лишь неадекватностью математической модели реальному функционированию системы.
2. Единственность решения. Ответ на вопрос о единственности решения уравнения (2.14) с симметричным ядром в классе  дается теоремой Пикара [21] о сходимости ряда (2.2). Для однозначного решения здесь существенно важным оказывается условие полноты системы собственных функций ядра дается теоремой Пикара [21] о сходимости ряда (2.2). Для однозначного решения здесь существенно важным оказывается условие полноты системы собственных функций ядра  [21]. [21].
Пусть, например, существуют не равные нулю почти всюду функции  , …, , …, 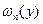 такие, что такие, что
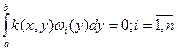 . .
Тогда если  – решение уравнения (2.14), то функция – решение уравнения (2.14), то функция
 , ,
где  – произвольные постоянные, также будет решением этого уравнения и, следовательно, решение определяется неоднозначно. – произвольные постоянные, также будет решением этого уравнения и, следовательно, решение определяется неоднозначно.
Для однозначного восстановления сигнала необходимы какие-то принципы отбора единственного «истинного» решения среди всех возможных, основанные на дополнительной априорной информации о сигнале. В частности можно воспользоваться методами интерполяции и экстраполяции функций, если дополнительная информация позволяет как-то ограничить класс возможных функций и ее можно использовать для устранения неоднозначности решения. Интересно, что даже на первый взгляд незначительная дополнительная информация, например информация о протяженности (длительности) восстанавливаемого сигнала, позволяет снять неопределенность решения [6, с.81].
3. Устойчивость решения. До сих пор мы не интересовались точностью измерения отклика системы, полагая, что правая часть интегрального уравнения (2.14) известна точно, без ошибок. На практике ошибки измерения неизбежны и вместо уравнения с точно известной правой частью  приходится решать это уравнение с приближенной правой частью приходится решать это уравнение с приближенной правой частью  известной, например, с точностью известной, например, с точностью  : :
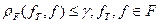 . .
Это было бы вполне приемлемо, если решение уравнения (2.14) было бы устойчиво к малым изменениям правой части.
Строгое определение устойчивости решения состоит в следующем [4]. Пусть каждому элементу  отвечает единственное решение отвечает единственное решение  Φ, получаемое по некоторому правилу Φ, получаемое по некоторому правилу  . Тогда решение . Тогда решение  из пространства Φ по исходным данным из пространства Φ по исходным данным  из пространства F называется устойчивым (на этих пространствах), если для любого из пространства F называется устойчивым (на этих пространствах), если для любого  можно указать такое число можно указать такое число 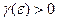 , что из неравенства , что из неравенства  следует следует  , где , где  ; ;   , ,  Φ. Φ.
В таком определении решение интегрального уравнения Фредгольма 1-го рода с ядром, принадлежащим  или или  , оказывается неустойчивым. Это объясняется тем, что оператор уравнения K, действующий в , оказывается неустойчивым. Это объясняется тем, что оператор уравнения K, действующий в  или в или в  и переводящий функцию и переводящий функцию 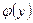 в функцию в функцию  по правилу по правилу
K  , ,
является вполне непрерывным оператором: он отображает всякое ограниченное множество элементов  в компактное множество элементов {K в компактное множество элементов {K  }. Критерием того, что оператор K является вполне непрерывным, обычно может служить условие [22]: }. Критерием того, что оператор K является вполне непрерывным, обычно может служить условие [22]:
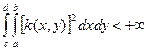 , ,
которое соблюдается для весовых функций реальных систем.
Вместе с тем одним из существенных моментов в теории интегральных уравнений является то, что оператор, обратный вполне непрерывному, не ограничен [21]. Поэтому, если  – два близких между собой элемента из пространства F и оба уравнения K – два близких между собой элемента из пространства F и оба уравнения K  =f1 и K =f1 и K  =f2 разрешимы, то соответствующие решения =f2 разрешимы, то соответствующие решения 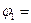 K-1 f1 и K-1 f1 и 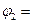 K-1 f2 могут сильно различаться друг от друга в пространстве Φ. K-1 f2 могут сильно различаться друг от друга в пространстве Φ.
Таким образом, сколь угодно малая погрешность в определении правой части уравнения (2.14) может привести к сколь угодно большой ошибке решения.
Не нашли, что искали? Воспользуйтесь поиском по сайту:
©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|


 (2.14)
(2.14) и на правую часть
и на правую часть  .решение может не существовать вообще, либо существовать не для всякой правой части. Например, если ядро имеет непрерывную производную по х, то и правая часть уравнения также должна иметь непрерывную производную по х. Если же правая часть содержит точки, в которых функция
.решение может не существовать вообще, либо существовать не для всякой правой части. Например, если ядро имеет непрерывную производную по х, то и правая часть уравнения также должна иметь непрерывную производную по х. Если же правая часть содержит точки, в которых функция 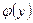 и отклик
и отклик  Φ.
Φ. .
.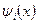 ядра
ядра  .
.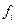 – коэффициенты разложения функции
– коэффициенты разложения функции 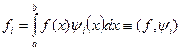 ,
, ,
,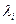 – собственные значения (собственные числа) ядра
– собственные значения (собственные числа) ядра 
 и
и 
 ,
, 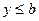 ), то уравнение (2.14) имеет решение, принадлежащее
), то уравнение (2.14) имеет решение, принадлежащее 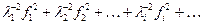 (2.15)
(2.15) . Например, если ядро
. Например, если ядро  , (2.16)
, (2.16)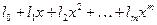
 , то уравнение имеет решение только для таких правых частей
, то уравнение имеет решение только для таких правых частей  , то при данном ядре (2.16) уравнение (2.14) не имеет решения.
, то при данном ядре (2.16) уравнение (2.14) не имеет решения. , …,
, …, 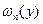 такие, что
такие, что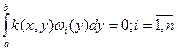 .
. – решение уравнения (2.14), то функция
– решение уравнения (2.14), то функция ,
, – произвольные постоянные, также будет решением этого уравнения и, следовательно, решение определяется неоднозначно.
– произвольные постоянные, также будет решением этого уравнения и, следовательно, решение определяется неоднозначно. приходится решать это уравнение с приближенной правой частью
приходится решать это уравнение с приближенной правой частью  :
: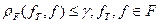 .
. отвечает единственное решение
отвечает единственное решение  Φ, получаемое по некоторому правилу
Φ, получаемое по некоторому правилу  . Тогда решение
. Тогда решение  из пространства Φ по исходным данным
из пространства Φ по исходным данным  из пространства F называется устойчивым (на этих пространствах), если для любого
из пространства F называется устойчивым (на этих пространствах), если для любого  можно указать такое число
можно указать такое число 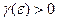 , что из неравенства
, что из неравенства  следует
следует  , где
, где  ;
; 
 ,
,  Φ.
Φ. ,
, в компактное множество элементов {K
в компактное множество элементов {K 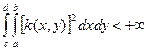 ,
, – два близких между собой элемента из пространства F и оба уравнения K
– два близких между собой элемента из пространства F и оба уравнения K 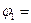 K-1 f1 и
K-1 f1 и 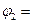 K-1 f2 могут сильно различаться друг от друга в пространстве Φ.
K-1 f2 могут сильно различаться друг от друга в пространстве Φ.