
|
|
Обратные некорректные задачиУсловно все задачи математической физики можно поделить на прямые и обратные. К прямым задачам математической физики относят задачи, ориентированные по ходу причинно-следственной связи, т.е. задачи разыскания следствий заданных причин, например, вычисление реакций прибора по известному сигналу на входе. Обратными задачами в этом понимании оказываются задачи, связанные с обращением причинно-следственной связи, т.е. задачи отыскания причин известных следствий – восстановление входного сигнала по реакции на выходе прибора. Обратные задачи возникают обычно как задачи интерпретации тех или иных наблюдений. Собственно говоря, любая задача измерения тех или иных характеристик физического объекта есть обратная задача в смысле данного определения. Однако имеется тенденция использовать термин «обратная задача» для обозначения достаточно сложных задач интерпретации, когда либо одновременно и не независимым образом измеряют много параметров физического объекта, либо число этих параметров вообще неопределенно велико (если состояние объекта описывается, например, некоторой функцией координат). Введем некоторые фундаментальные понятия, широко используемые в теории решения обратных задач, а именно: сигнал, обработка сигналов, восстановление и разрешение сигналов. Сигнал – это некоторое средство для передачи информации. Любое измерение, полученное экспериментатором, может быть названо сигналом. Определение слова сигнал в разных дисциплинах разное. С точки зрения исследователя сигнал может быть определен как отклик устройства на определенное воздействие. Сигналы могут измеряться как функции одного или нескольких параметров (времени, длины волны и т.п.). Целью обработки сигналовявляется извлечение информации. Следует иметь в виду, что обработка не может увеличить объем информации, однако она может преобразовать ее в такую форму, что наблюдатель сможет легко расшифровать информацию. Обработка сигналов включает в себя две основные задачи – преобразование способа представления информации в сигнале и сокращение ее объема. Первый класс задач включает улучшение визуального качества сигналов, спектральный анализ, коррекцию и т.п. Сокращение объема информации заключается в удалении ненужной информации. Каждый исследователь хотел бы пользоваться в своей работе идеальными приборами, т.е. приборами, которые не вносят искажений в результат наблюдения исследуемых процессов и явлений. На практике вместо истинного сигнала, который можно получить от идеального прибора, мы обычно наблюдаем некоторый искаженный сигнал. Устранение искажений, вносимых реальными приборами, требуется в самых различных областях науки и техники: оптике, спектроскопии, аналитической химии и т.д. Существуют два принципиально различающихся способа устранения искажений. Первый, который можно назвать априорным, состоит в том, что при помощи искусных технических решений совершенствуют конструкцию реального прибора, добиваясь минимума искажений в системе приема сигнала. Этот способ в основном используется в современной измерительной технике. Но возможности технического совершенствования аппаратуры не всегда безграничны. По мере улучшения технических характеристик неизбежно возрастают сложность и стоимость аппаратуры. Кроме того, сами процессы наблюдения (измерения) обычно связаны с различными неконтролируемыми факторами, искажающее влияние которых нельзя устранить никаким конструктивным улучшением аппаратуры. Примером такого фактора может служить влияние атмосферы на процесс съемки звездного неба с помощью телескопа. Другой способ устранения искажений, который будет называться апостериорным, заключается в восстановлении самих сигналов. Под восстановлением сигнала будем понимать такую обработку отклика на выходе прибора, которая позволяет получать функцию, наиболее близкую (по тому или иному критерию) к истинному входному сигналу. Процесс восстановления предусматривает апостериорное обращение тех этапов формирования сигнала, которые вызвали его искажение. При этом реальные явления, вызывающие искажения, заменяются их математической моделью. Результат такого восстановления можно рассматривать как данные измерений, полученные на некотором гипотетическом приборе, предельные возможности которого могут быть существенно выше, чем у исходного. Восстановление сигналов становится исключительно актуальной проблемой в свете повышения эффективности и качества научных исследований и производства. Разрешение можно определить как процесс, при котором сложный сигнал разлагается на составляющие. В физике и технике широко используется понятие линейной системы (линейного прибора). Обозначим через – при усилении входного сигнала без изменения его формы в k раз форма выходного сигнала также не должна изменяться, а амплитуда должна увеличиваться в k раз. – при подаче на вход системы суммы сигналов отклик системы должен быть равен аналогичной сумме выходных сигналов, соответствующих отдельным воздействиям. Для оператора L, ставящего в соответствие каждому входному сигналу L [ В линейных системах соотношения между изменениями физических величин обычно выражаются линейными дифференциальными уравнениями. Несмотря на то, что большинство реальных систем являются принципиально нелинейными, часто приходится прибегать к тем или иным методам линеаризации исходных уравнений и затем проводить исследования в классе линейных систем. Различие между процессами в линейных и нелинейных системах сводится к тому, что при анализе линейных систем (в силу свойства суперпозиции по частным процессам) можно сделать вполне определенное заключение о всех возможных в данной системе процессах, а для процессах в нелинейных системах этого сделать нельзя. Рассмотрим обыкновенное дифференциальное уравнение порядка n с переменными коэффициентами
и соответствующее ему операторное уравнение с дифференциальным оператором D : Df(x)= которые связывают выходной и входной сигналы некоторой линейной системы. Допустим сначала, что граничные условия отсутствуют, и существует некоторый оператор K такой, что DK=I, где I – единичный оператор. Тогда, по крайней мере формально, можно записать: f(x)= K Выясним смысл оператора K, полагая, что входным воздействием служит единичный импульс, приложенный в некоторой точке x=y, т.е. сигналом является функция Дирака Dk(x,y)= Если существует обратный оператор, то отклик должен быть равен k(x,y)=K Представляя
Учитывая равенство (1.1.6), находим
Таким образом, K – интегральный оператор с ядром k(x,y). Интеграл вида (2.7) обычно выражает частное решение уравнения (2.2), соответствующее основному закону функционирования линейной системы в установившемся режиме. Для получения общего решения к частному решению необходимо добавить все решения однородного уравнения Df(x)=0, (2.8) характеризующие переходные процессы в системе. Если область изменения независимых переменных ограничена некоторым промежутком [a,b] и заданы определенные граничные условия (начальные или краевые), то общее решение уравнения (2.2) в предположении о непрерывности всех коэффициентов
где Иногда удается определить функцию k(x,y) таким образом, что сумма в правой части выражения (1.1.9) становится исчезающе малой и частное решение
оказывается одновременно и общим решением уравнения (2.2). Функцию k(x,y) еще называют весовой функцией линейной системы. Дополнительные условия, налагаемые на функцию k(x,y), а также пределы интегрирования в (2.10) обычно определяются сущностью задачи. Если бы коэффициенты
Уравнение (2.11) представляет собой интегральное уравнение Фредгольма 1-го рода с ядром k(x,y), которое определяет оператор K прямой задачи, переводящий неизвестную функцию K Будем называть уравнение типа (2.11) основным интегральным уравнением обратной задачи, а уравнение (2.12) – основным операторным уравнением. Часто удобно допустить, что ядро уравнения Фредгольма является разностным ядром, т.е. k(x,y)=k(x-y). Такое допущение широко используется в различных физических и технических прикладных задачах и означает, что форма отклика системы на импульсное воздействие по условию не зависит от того. В какой точке области изменения независимой переменной приложен импульс. Линейные системы, удовлетворяющие этому условию, в теории систем называют однородными или инвариантными к сдвигу. Основной закон функционирования однородных систем выражается линейными дифференциальными уравнениями, а основное интегральное уравнение является уравнением типа свертки:
На функции сигнала и отклика наложим некоторые условия – будем считать их вещественными функциями – элементами некоторых метрических пространств Φ и F с расстояниями между элементами Класс
Расстояние между двумя функциями,
Класс
Расстояние в
Здесь всюду интеграл понимается в смысле интеграла Лебега. Класс
При решении обратных задач естественно возникают три следующих вопроса: существует ли решение основного интегрального уравнения? если решение существует, то является ли оно единственным? устойчиво ли решение, т.е. приводят ли малые изменения исходных данных соответственно к малым изменениям решения? Если ответ на все эти вопросы положительный, то задача называется корректно поставленной. В противном случае задачу называют некорректно поставленной или просто некорректной. Задачи восстановления сигналов, как правило, оказываются некорректными. Понятие корректности впервые ввел Ж.Адамар [16,17]. Позднее А.Н.Тихонов [4] сформулировал новое определение корректности, которое М.М.Лаврентьев [18] назвал корректностью по Тихонову. Задача решения уравнения (2.12) называется условно корректной или корректной по Тихонову, если [4,18-20]: априори известно, что решение решение единственно в классе функций, принадлежащих М; бесконечно малым вариациям f, не выводящим решение Отличие условной корректности от классической заключается во введении множества корректности, существенно сужающего класс возможных решений. Наиболее характерный пример множества корректности – компакт. Однако в большинстве прикладных задач класс возможных решений Φ не является компактом, т.е. на решение нельзя наложить, исходя из физических соображений, жесткие ограничения и, кроме того, изменения правой части f уравнения (2.12), обусловленные ее погрешностями, могут выводить f за пределы множества KΦ. Такие задачи иногда называют существенно некорректными [4]. В течение долгого времени считалось, что некорректные задачи лишены физического смысла и их не имеет смысла решать. Однако имеется много важных задач физики, техники, геологии и т.д., математически описываемых адекватно и тем не менее являющихся некорректными, что сделало актуальной проблему разработки эффективных методов их решения. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 входной сигнал (или просто сигнал), а через
входной сигнал (или просто сигнал), а через  - выходной сигнал (или отклик). Если система линейна, то она обладает свойством суперпозиции сигналов, которое предусматривает выполнение следующих требований:
- выходной сигнал (или отклик). Если система линейна, то она обладает свойством суперпозиции сигналов, которое предусматривает выполнение следующих требований: ]=
]= 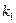 L [
L [  ]+
]+  L [
L [  ]+…+
]+…+  L [
L [  ]==
]==  ;
;  Φ;
Φ;  F (2.1)
F (2.1) (2.2)
(2.2) . Тогда результирующий выходной сигнал k, как отклик системы в точке x на импульсный входной сигнал в точке y, является функцией двух независимых переменных x и y и должен удовлетворять уравнению
. Тогда результирующий выходной сигнал k, как отклик системы в точке x на импульсный входной сигнал в точке y, является функцией двух независимых переменных x и y и должен удовлетворять уравнению K[
K[  ]dy.
]dy. (2.7)
(2.7) и функции
и функции  , (2.9)
, (2.9) – линейно-независимые решения однородного уравнения (2.8),
– линейно-независимые решения однородного уравнения (2.8), 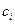 – постоянные, определяемые по граничным условиям.
– постоянные, определяемые по граничным условиям. (2.10)
(2.10) = f (2.12)
= f (2.12) (2.13)
(2.13) и
и  соответственно. Мы будем иметь дело главным образом с функциями, принадлежащими пространствам (классам)
соответственно. Мы будем иметь дело главным образом с функциями, принадлежащими пространствам (классам)  ,
,  и
и  .
. , интегрируемых на промежутке [a,b] (-
, интегрируемых на промежутке [a,b] (-  ) т.е. таких, что
) т.е. таких, что .
. и
и  , принадлежащих
, принадлежащих  )
) .
. .
.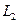 )
) .
. .
. М;
М;