|
Внецентренно сжатые стержни
Внецентренно сжатые и сжато-изогнутые стержни можно напрягать со стороны растяжения от действия изгибающего момента. Такие стержни могут быть в стойках и ригелях рам, в колоннах и т. п. По сравнению с изгибаемыми элементами (балками) работа и расчет внецентренно сжатых стержней сложнее, так как здесь появляется еще один дополнительный параметр — сжимающая сила 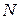 . .
Напряженное состояние сечения сплошного стержня при предварительном напряжении и последующем загружении показано на рис. 2.17. Методика подбора сечения, оптимального по расходу материала, разработана Л. В. Венковым (София).
Оптимальное сечение определяется значениями девяти параметров: 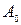 , , 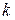 , ,  , , 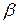 , ,  , ,   , ,  , ,  , где , где  – характеристика асимметрии сечения; – характеристика асимметрии сечения;  – гибкость стенки балки; – гибкость стенки балки;  ; ;  – коэффициент самонапряжения; – коэффициент самонапряжения; 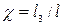 – относительная длина затяжки; – относительная длина затяжки;  – характеризует физические параметры материалов балки и затяжки. Значения остальных параметров даны на рис. 2.17. Коэффициентом – характеризует физические параметры материалов балки и затяжки. Значения остальных параметров даны на рис. 2.17. Коэффициентом  , определяющим положение затяжки по высоте сечения, следует задаваться по конструктивным соображениям в пределах , определяющим положение затяжки по высоте сечения, следует задаваться по конструктивным соображениям в пределах  . При большем значении . При большем значении  эффективность предварительного напряжения увеличивается, но вместе с тем затрудняются устройство анкерных креплений и обеспечение устойчивости стержня в процессе предварительного напряжения. Исходными уравнениями для анализа влияния различных параметров на получение оптимального сечения и разработки рабочей методики подбора сечений являются уравнения равновесия эффективность предварительного напряжения увеличивается, но вместе с тем затрудняются устройство анкерных креплений и обеспечение устойчивости стержня в процессе предварительного напряжения. Исходными уравнениями для анализа влияния различных параметров на получение оптимального сечения и разработки рабочей методики подбора сечений являются уравнения равновесия  и и  , получаемые из рассмотрения напряженного состояния сечения стержня. Уравнения равновесия при предварительном напряжении (рис. 2.17, б): , получаемые из рассмотрения напряженного состояния сечения стержня. Уравнения равновесия при предварительном напряжении (рис. 2.17, б):
 ; ; 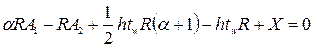 ; (2.19) ; (2.19)
 ; ;
 . (2.20) . (2.20)
При действии расчетной нагрузки (рис. 2.17, г)
 ; ;  ; (2.21) ; (2.21)
 ; ; 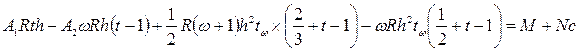 . (2.22) . (2.22)
Подстановкой в полученные уравнения различных параметров на ЭВМ было проанализировано их влияние на оптимальное сечение. Параметры  , , 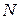 , , 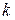 , ,  и и  принимаются заданными. Оптимальные параметры сечения в первую очередь зависят от коэффициента самонапряжения принимаются заданными. Оптимальные параметры сечения в первую очередь зависят от коэффициента самонапряжения 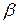 , который в свою очередь зависит от характера нагрузки, удаления затяжки от нижнего пояса и от физико-механических параметров стержня , который в свою очередь зависит от характера нагрузки, удаления затяжки от нижнего пояса и от физико-механических параметров стержня  . Получив формулу для значений усилий самонапряжения при изгибе сжатого стержня равномерно распределенной нагрузкой в функции геометрических и физико-механических параметров сечения стержня и затяжки, было проанализировано влияние этих параметров на оптимальное сечение стержня. . Получив формулу для значений усилий самонапряжения при изгибе сжатого стержня равномерно распределенной нагрузкой в функции геометрических и физико-механических параметров сечения стержня и затяжки, было проанализировано влияние этих параметров на оптимальное сечение стержня.
Полученные значения коэффициента самонапряжения 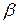 в функции параметров в функции параметров  , ,  и и  приведены в табл. 2.6 [1, с.34]. приведены в табл. 2.6 [1, с.34].
Из табл. 2.6 видно, что наибольшее влияние на коэффициент самонапряжения оказывают физико-механические характеристики затяжки и стержня. С ростом  коэффициент самонапряжения увеличивается незначительно, влияние коэффициент самонапряжения увеличивается незначительно, влияние  несколько больше. Анализ показал, что коэффициент несколько больше. Анализ показал, что коэффициент  незначительно отклоняется от значения 0,15 – 0,2. Коэффициент незначительно отклоняется от значения 0,15 – 0,2. Коэффициент  равен единице при больших значениях эксцентриситета и значениях равен единице при больших значениях эксцентриситета и значениях 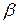 , близких к 1 – 1,4. При малых значениях , близких к 1 – 1,4. При малых значениях  и больших и больших 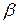 коэффициент коэффициент  может быть значительно меньше единицы, т. е. оптимальные параметры получаются при недонапряжении растянутых волокон в процессе нагружения. Параметр может быть значительно меньше единицы, т. е. оптимальные параметры получаются при недонапряжении растянутых волокон в процессе нагружения. Параметр  мало меняется и может быть принят, как и для изгибаемых элементов, равным 0,55. Площадь сечения уменьшается с увеличением параметров мало меняется и может быть принят, как и для изгибаемых элементов, равным 0,55. Площадь сечения уменьшается с увеличением параметров  и и 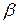 . При изгибе стержня равномерно распределенной нагрузкой длина затяжки . При изгибе стержня равномерно распределенной нагрузкой длина затяжки 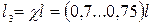 . .
Для практического применения составлена табл. 2.7 [1, с.35] расчетных параметров, с помощью которых можно легко подбирать сечения предварительно напряженных сжато-изогнутых стержней.
Методика подбора сечения стержня с оптимальными параметрами сводится к следующему:
1. Из табл. 2.7, задаваясь гибкостью стенки 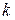 , и, интерполируя по известному , и, интерполируя по известному  , находим значения параметров , находим значения параметров 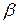 , ,  , ,  , , 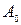 , ,  , , 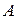 , ,  , ,  . .
2. Используя формулы (3.15) безразмерных величин несимметричного двутавра, компонуем сечение стержня и проверяем прочность в стадии предварительного напряжения и под нагрузкой.
Результаты пробного проектирования показали, что экономия массы от применения предварительного напряжения составляет 9 – 16 %. Экономия возрастает с увеличением параметров  и и  и с уменьшением параметра и с уменьшением параметра  . .
Не нашли, что искали? Воспользуйтесь поиском по сайту:
©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|


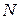 .
.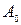 ,
, 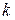 ,
,  ,
, 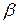 ,
,  ,
, 
 ,
,  ,
,  , где
, где  – характеристика асимметрии сечения;
– характеристика асимметрии сечения;  – гибкость стенки балки;
– гибкость стенки балки;  ;
;  – коэффициент самонапряжения;
– коэффициент самонапряжения; 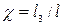 – относительная длина затяжки;
– относительная длина затяжки;  . При большем значении
. При большем значении  и
и  , получаемые из рассмотрения напряженного состояния сечения стержня. Уравнения равновесия при предварительном напряжении (рис. 2.17, б):
, получаемые из рассмотрения напряженного состояния сечения стержня. Уравнения равновесия при предварительном напряжении (рис. 2.17, б):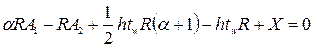 ; (2.19)
; (2.19) . (2.20)
. (2.20) ; (2.21)
; (2.21)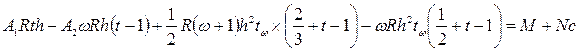 . (2.22)
. (2.22) ,
,  и
и  и больших
и больших  мало меняется и может быть принят, как и для изгибаемых элементов, равным 0,55. Площадь сечения уменьшается с увеличением параметров
мало меняется и может быть принят, как и для изгибаемых элементов, равным 0,55. Площадь сечения уменьшается с увеличением параметров  и
и 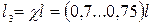 .
.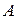 ,
,  ,
,