
|
|
Конструкция и расчет центрально сжатых стержнейГибкие стержни, работающие на центральное сжатие, можно усилить предварительно напряженным шпренгелем, значительно повысив тем самым его несущую способность и облегчив конструкцию. Шпренгельные системы могут иметь разнообразные схемы (рис. 2,12). Конструкция состоит из центрального стержня (чаще всего трубы) и четырехстороннего шпренгеля, который обеспечивает пространственную жесткость. Тяги шпренгельной системы натягиваются, что обеспечивает их работу в момент потери стержнем устойчивости как со стороны растяжения, так и сжатия. Распорки шпренгеля должны быть жестко соединены со стойкой и иметь достаточную изгибную жесткость (рис. 2.13). Центральный стержень работает как стойка, имеющая упругие опоры в местах прикрепления распорок шпренгеля. Тяги прикрепляются к концам распорок, чтобы устранить проскальзывание их в момент изгиба стержня. Тяги могут быть из стальных канатов, семипроволочных прядей или круглой арматуры. В СССР построены мачты, состоящие из одной секции нескольких последовательно сопряженных однотипных секций, поддерживаемых в вертикальном положении оттяжками (рис. 2.14). Каждая секция представляет собой стойку, усиленную с четырех сторон предварительно напряженными шпренгельными системами. Такие мачты высотой до 164 м оказались весьма экономичными по расходу металла и удобными в монтаже. Расчёт стержней, усиленных предварительно напряженными шпренгелями, разработан А. А. Воеводиным [2].
Рис. 2.12. Предварительно напряжённые шпренгельные стойки
Рис. 2.13. Сборка на стеллажах с предварительно напряженным шпренгелем
Рис. 2.14. Многоярусные мачты шпренгельной системы Расчетная схема многопанельных стержней принимается в виде центрально-сжатого стержня с упругоподатливыми опорами в месте прикрепления распорок шпренгеля (рис. 2.15). Упругоподатливые опоры препятствуют свободному горизонтальному перемещению и повороту соответствующих сечений при искривлении стержня от приложения критической силы. При жестких распорках стержень теряет устойчивость по первой (рис. 2.15,б), а при недостаточной их жесткости по второй (рис. 2.15, в) кривой Эйлера. При потере устойчивости по второй кривой Эйлера критическая сила заметно уменьшается.
Рис. 2.15. Расчётная схема двухпанельной предварительно напряжённой шпренгельной стойки а – конструктивная схема; б – потеря устойчивости по первой схеме; в – потеря устойчивости по второй схеме; г – сечение распорки Исходя из устойчивости одной панели стержня с расчетной длиной При заданном коэффициенте запаса общей устойчивости
коэффициент Из уравнения
определяем площадь тяги. Тяга принимается из круглой стали. Зная
находим площадь сечения ветвей распорок При предварительном напряжении стержня параллельными тягами задача устойчивости сводится к нахождению критической силы сжатого стержня с разгружающими моментами на концах. При потере стержнем устойчивости жесткие диафрагмы поворачиваются на угол
Рис. 2.16. К расчёту предварительно напряжённой стойки с параллельными тягами Эти усилия создают по концам стержня моменты, обратные по знаку моментам, возникающим в стержне при потере устойчивости.
Критическая сила в стержне определяется по формуле
Мощные тяги могут обеспечить полное защемление концов стержня, при этом
Коэффициент
Зная
Рис. 2.17. Эпюра нормальных напряжений внецентренно сжатого стержня при предварительном напряжении и нагружении а – сечение стержня; б – напряжение от усилия в затяжке; в – напряжения от нагрузки; г – суммарные напряжения при действии расчётной нагрузки
Варьируя расстояние
В формулах (2.14) - (2.18): 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
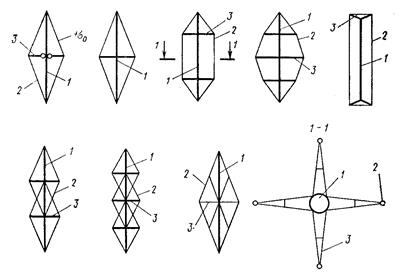
 1 – стержень; 2 – тяга; 3 - распорка
1 – стержень; 2 – тяга; 3 - распорка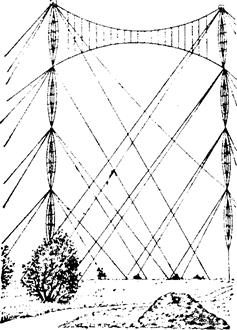
 Двухпанельный стержень, усиленный четырехсторонним шпренгелем, рассчитывают по следующей схеме. Заданными являются расчетная нагрузка
Двухпанельный стержень, усиленный четырехсторонним шпренгелем, рассчитывают по следующей схеме. Заданными являются расчетная нагрузка  и остаточные натяжения
и остаточные натяжения 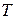 в каждой из четырех тяг после нагружения стержня; высота стержня
в каждой из четырех тяг после нагружения стержня; высота стержня  ; угол наклона тяг
; угол наклона тяг  ; расчетное сопротивление
; расчетное сопротивление  и модуль упругости материала
и модуль упругости материала  ; коэффициенты условия работы
; коэффициенты условия работы 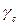 и надежности по нагрузке;
и надежности по нагрузке;  ; запас общей устойчивости
; запас общей устойчивости  .
.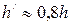 , находим гибкость
, находим гибкость  и по гибкости – требуемый наружный диаметр трубы
и по гибкости – требуемый наружный диаметр трубы  . Подбираем трубу по ГОСТу и получаем ее геометрические характеристики:
. Подбираем трубу по ГОСТу и получаем ее геометрические характеристики:  ,
,  ,
, 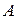 ,
,  ,
,  . Определяем допустимую вертикальную нагрузку
. Определяем допустимую вертикальную нагрузку  для подобранной трубы высотой
для подобранной трубы высотой  , найдя по гибкости
, найдя по гибкости 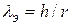 коэффициент
коэффициент  . Тогда расчетная нагрузка на шпренгельную стойку
. Тогда расчетная нагрузка на шпренгельную стойку  (полная допустимая нагрузка минус остаточные натяжения в тягах).
(полная допустимая нагрузка минус остаточные натяжения в тягах). получим критическую нагрузку шпренгельной стойки
получим критическую нагрузку шпренгельной стойки  и, исходя из формулы
и, исходя из формулы –
– .
. (2.12)
(2.12) и
и  из уравнения
из уравнения (2.13)
(2.13) и подбираем их сечение (обычно из сдвоенных уголков). Если уменьшить сечение ветвей распорок, то стержень может потерять устойчивость по двум полуволнам, и критическая нагрузка несколько уменьшится.
и подбираем их сечение (обычно из сдвоенных уголков). Если уменьшить сечение ветвей распорок, то стержень может потерять устойчивость по двум полуволнам, и критическая нагрузка несколько уменьшится. . (2.14)
. (2.14)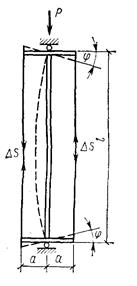
 (2.15)
(2.15) (2.16)
(2.16) , а критическая сила
, а критическая сила (2.16')
(2.16') . (2.17)
. (2.17) и геометрические параметры
и геометрические параметры  ,
,  ,
,  , можно по формулам (2.16) и (2.17) подобрать сечение стержня.
, можно по формулам (2.16) и (2.17) подобрать сечение стержня.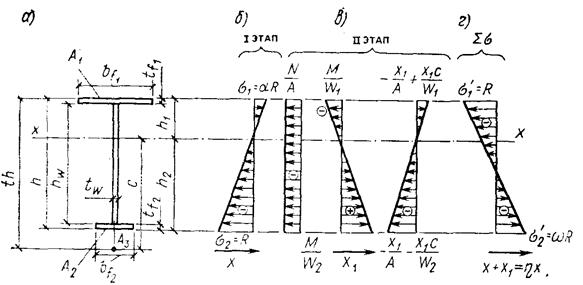
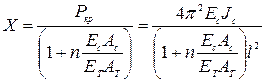 . (2.18)
. (2.18) ,
,  – модуль упругости и площадь стержня;
– модуль упругости и площадь стержня;  ,
,  – число тяг.
– число тяг.