Максимальное ослабление света происходит в тех точках пространства, где суммируются волны, имеющие оптическую разность хода, равную нечетному числу длин полуволн
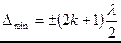 (3) (3)
где k = 0, 1, 2, 3... и т.д.
При всех промежуточных значениях разности хода будет иметь место частичное усиление или ослабление света.
Интерференцию света можно наблюдать при отражении его от тонких пленок. Примером интерференции света в тонких пленках являются цветные разводы масла, бензина на лужах, мыльные пузыри, оперения птиц, крылья бабочек, цвета побежалости на металлах и т. д. Интерференция света втонких пленках представляет большой практический интерес.
Рассмотрим процесс образования интерференции света на тонкой пленке. Пусть имеется тонкая плоскопараллельная пластинка (Рис. 1), толщиною d с относительным показателем преломления п.
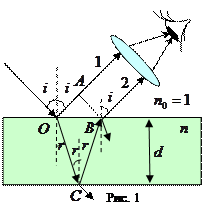 На пластинку падает луч света под углом На пластинку падает луч света под углом 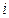 . Лучи 1 и2 когерентны. Разность хода между ними возникает в области от точки O до плоскости AB, которая перпендикулярна лучам 1 и 2. Из геометрии рис. 1 видно, что . Лучи 1 и2 когерентны. Разность хода между ними возникает в области от точки O до плоскости AB, которая перпендикулярна лучам 1 и 2. Из геометрии рис. 1 видно, что
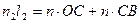 (4); (4); 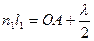 (5) (5)
Слагаемое 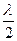 в уравнении (5) возникает из-за того, что при отражении света от оптически более плотной среды происходит потеря половины длины волны, путь света как бы увеличивается на в уравнении (5) возникает из-за того, что при отражении света от оптически более плотной среды происходит потеря половины длины волны, путь света как бы увеличивается на 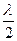 вследствие того, что электромагнитное поле вещества захватывает электромагнитное поле световой волны. Вычитая (5) из (4), получаем оптическую разность хода: вследствие того, что электромагнитное поле вещества захватывает электромагнитное поле световой волны. Вычитая (5) из (4), получаем оптическую разность хода:
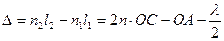 (6) (6)
Из геометрии рисунка и с учетом закона преломления 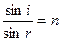 можно получить следующее выражение для оптической разности хода лучей на тонкой пленке в отраженных лучах можно получить следующее выражение для оптической разности хода лучей на тонкой пленке в отраженных лучах
 (7) (7)
Оптическая разность хода 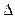 зависит от толщины пленки d, ее относительного показателя преломления зависит от толщины пленки d, ее относительного показателя преломления 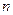 , угла падения , угла падения 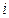 света на пленку и длины волны света света на пленку и длины волны света 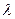 . При выполнении условия (2) получаются интерференционные максимумы, при выполнении условия (3) - минимумы. При интерференции света на тонкой пленке . При выполнении условия (2) получаются интерференционные максимумы, при выполнении условия (3) - минимумы. При интерференции света на тонкой пленке  и в общем случае одновременно могут изменяться все четыре параметра. Но в некоторых случаях хотя бы два из них могут оставаться постоянными. В зависимости от этого различают интерференционные полосы равной толщины и равного наклона. и в общем случае одновременно могут изменяться все четыре параметра. Но в некоторых случаях хотя бы два из них могут оставаться постоянными. В зависимости от этого различают интерференционные полосы равной толщины и равного наклона.
Интерференционные полосы равного наклонанаблюдаются, когда d = const, n = const. Из уравнения (7) при 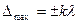 следует, что угол следует, что угол 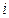 пропорционален длине волны пропорционален длине волны 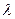 . С изменением угла падения света . С изменением угла падения света 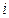 на пленку условия максимума будут выполняться для света различных длин волн, в результате пленка под различными углами будет казаться окрашенной в различные цвета. на пленку условия максимума будут выполняться для света различных длин волн, в результате пленка под различными углами будет казаться окрашенной в различные цвета.
Интерференционные полосы равной толщинынаблюдаются на пленке в виде клина (мыльные пузыри) или ступенек, когда  и и 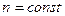 . Тогда с изменением толщины d плёнки, согласно уравнению (7), условия максимума будут выполняться для света различных длин волн . Тогда с изменением толщины d плёнки, согласно уравнению (7), условия максимума будут выполняться для света различных длин волн 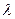 . Пленка на различных толщинах будет казаться окрашенной в различные цвета. . Пленка на различных толщинах будет казаться окрашенной в различные цвета.
 Рассмотрим один из примеров практического использования явления интерференции, при котором представляется возможным или найти параметры экспериментальной установки, или определить длину волны используемого света. Рассмотрим один из примеров практического использования явления интерференции, при котором представляется возможным или найти параметры экспериментальной установки, или определить длину волны используемого света.
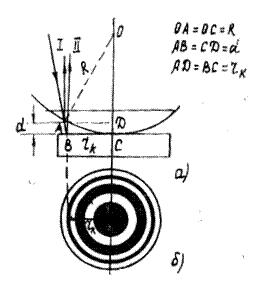
Примером интерференционных полос равной толщины являются кольца Ньютона(Рис. 2, б), которые наблюдаются при интерференции света на воздушном клине между плоскопараллельной стеклянной пластинкой и плосковыпуклой линзой большого радиуса кривизны R. Процесс образования когерентных лучей показан на рис. 2, а. Оптическая разность хода между когерентными лучами I и II
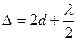 (8) (8)
где d - толщина воздушного клина на расстоянии 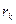 от центра С. Из треугольника ОАD получаем от центра С. Из треугольника ОАD получаем
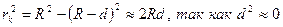 . .
Отсюда 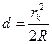 (9) (9)
Оптическая разность хода 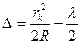 (10) (10)
При 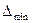 получаются темные кольца Ньютона. Радиусы темных колец Ньютона в отраженном свете получаются темные кольца Ньютона. Радиусы темных колец Ньютона в отраженном свете  (11), (11),
где k = 0, 1, 2, 3... Радиусы светлых колец Ньютона в отраженном свете:
 (12) (12)
Из формул (11) и (12)следует, чем больше k, тем меньше различие между радиусами соседних колец и тем теснее расположены кольца. Наблюдая кольца Ньютона с помощью специальных пробных колец, широко применяющихся в оптической промышленности, можно измерять радиусы R кривизны поверхностей линз, контролировать правильность формы плоских и сферических поверхностей.
По измеренным радиусам колец Ньютона, используя формулу (11), можно определить длину световой волны 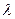 если известен радиус кривизны линзы R. Однако вследствие упругой деформации стекла невозможно добиться идеального соприкосновения сферической линзы и плоской пластинки в одной точке. Поэтому результат получится более точным, если если известен радиус кривизны линзы R. Однако вследствие упругой деформации стекла невозможно добиться идеального соприкосновения сферической линзы и плоской пластинки в одной точке. Поэтому результат получится более точным, если 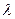 вычислять по разности радиусов двух колец: вычислять по разности радиусов двух колец: 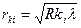 (13) (13)
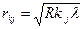 (14) (14)
Совместное решение уравнений (13) и (14)дает длину световой волны
 (15) (15)
Не нашли, что искали? Воспользуйтесь поиском по сайту:
©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|


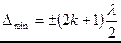 (3)
(3) На пластинку падает луч света под углом
На пластинку падает луч света под углом 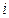 . Лучи 1 и2 когерентны. Разность хода между ними возникает в области от точки O до плоскости AB, которая перпендикулярна лучам 1 и 2. Из геометрии рис. 1 видно, что
. Лучи 1 и2 когерентны. Разность хода между ними возникает в области от точки O до плоскости AB, которая перпендикулярна лучам 1 и 2. Из геометрии рис. 1 видно, что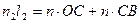 (4);
(4); 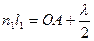 (5)
(5)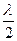 в уравнении (5) возникает из-за того, что при отражении света от оптически более плотной среды происходит потеря половины длины волны, путь света как бы увеличивается на
в уравнении (5) возникает из-за того, что при отражении света от оптически более плотной среды происходит потеря половины длины волны, путь света как бы увеличивается на 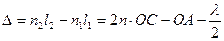 (6)
(6)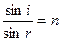 можно получить следующее выражение для оптической разности хода лучей на тонкой пленке в отраженных лучах
можно получить следующее выражение для оптической разности хода лучей на тонкой пленке в отраженных лучах (7)
(7)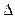 зависит от толщины пленки d, ее относительного показателя преломления
зависит от толщины пленки d, ее относительного показателя преломления 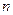 , угла падения
, угла падения 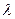 . При выполнении условия (2) получаются интерференционные максимумы, при выполнении условия (3) - минимумы. При интерференции света на тонкой пленке
. При выполнении условия (2) получаются интерференционные максимумы, при выполнении условия (3) - минимумы. При интерференции света на тонкой пленке  и в общем случае одновременно могут изменяться все четыре параметра. Но в некоторых случаях хотя бы два из них могут оставаться постоянными. В зависимости от этого различают интерференционные полосы равной толщины и равного наклона.
и в общем случае одновременно могут изменяться все четыре параметра. Но в некоторых случаях хотя бы два из них могут оставаться постоянными. В зависимости от этого различают интерференционные полосы равной толщины и равного наклона.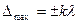 следует, что угол
следует, что угол  и
и 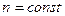 . Тогда с изменением толщины d плёнки, согласно уравнению (7), условия максимума будут выполняться для света различных длин волн
. Тогда с изменением толщины d плёнки, согласно уравнению (7), условия максимума будут выполняться для света различных длин волн  Рассмотрим один из примеров практического использования явления интерференции, при котором представляется возможным или найти параметры экспериментальной установки, или определить длину волны используемого света.
Рассмотрим один из примеров практического использования явления интерференции, при котором представляется возможным или найти параметры экспериментальной установки, или определить длину волны используемого света.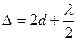 (8)
(8)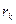 от центра С. Из треугольника ОАD получаем
от центра С. Из треугольника ОАD получаем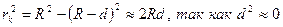 .
.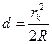 (9)
(9)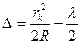 (10)
(10)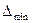 получаются темные кольца Ньютона. Радиусы темных колец Ньютона в отраженном свете
получаются темные кольца Ньютона. Радиусы темных колец Ньютона в отраженном свете  (11),
(11), (12)
(12)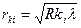 (13)
(13)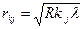 (14)
(14) (15)
(15)