
|
|
Краткие теоретические сведенияЛинзой называется прозрачное для света отшлифованное тело, ограниченное двумя криволинейными или криволинейной и плоской поверхностями. Линза называется тонкой, если её толщина мала по сравнению с радиусами кривизны её поверхностей. Линзы с действительными фокусами (положительной оптической силой) называются собирающими, с мнимыми фокусами (отрицательной оптической силой) - рассеивающими. Оптической силой линзы D называется величина обратная её фокусному расстоянию F:
R1 и R2 – радиусы кривизны первой и второй поверхности линзы (если поверхность выпуклая, то перед Т.о. если при расчетах по формуле (1) получается положительная оптическая сила, то линза является собирающей, если же оптическая сила, получается отрицательной, то линза является рассеивающей (т.е. одна и та же линзы в различных средах может являться и собирающей и рассеивающей). Изображение точки в линзе графически получается как точка пересечения двух любых преломленных лучей прошедших через линзу. Наиболее часто пользуются двумя лучами из трёх (см. рис.): 1 - падающий луч, параллельный главной оптической оси, преломляясь, он проходит через главный фокус (F); 2 - падающий луч, проходящий через главный фокус, преломляясь, он проходит параллельно главной оптической оси; 3 - луч, проходящий через оптический центр линзы, не изменяет своего направления, так как у оптического центра поверхности линзы практически параллельны. Расстояние от оптического центра линзы до главного фокуса называется фокусным расстоянием F. Расстояние от положения предмета на главной оптической оси линзы до оптического центра линзы принято обозначать d, а расстояние от оптического центра линзы до положения изображения на главной оптической оси f. При использовании введённых обозначений формула тонкой линзы имеет вид: где знак плюс перед D и Все изображения делятся на действительные (получаются на пересечении самих лучей (существуют в действительности)) и мнимые (получаются на пересечении продолжений лучей (в действительности не существуют)); прямые и перевёрнутые (обратные); увеличенные, уменьшенные и равные по величине предмету. Увеличение, даваемое линзой по определению равно: где H – высота изображения, h – высота предмета. Вторая часть этого равенства получается, если рассмотреть подобие треугольников (см. рис.). Если у двояковыпуклой линзы радиусы кривизны поверхностей одинаковы, то эти радиусы можно определить, используя формулу (1):
В формуле (4) мы приняли, что линза изготовлена из стекла ( Порядок выполнения работы: 1. С помощью мыши установить на оптической скамье фокусное расстояние линзы F (тем самым выбрать линзу) (см. варианты).
2. Установить предмет (стрелку) на определённом расстоянии d от линзы, таком, чтобы можно было измерить расстояние f от линзы до изображения. Замерить линейкой эти расстояния, а также высоту предмета h и изображения H. Охарактеризовать изображение (действительное или мнимое, прямое или перевёрнутое, увеличенное или уменьшенное). Записать полученные данные в таблицу 1. 3. Повторить пункт 2 ещё для шести положений предмета (не забывайте о знаке перед f, если изображение мнимое, то знак минус)
Обработка результатов измерений: 1. Рассчитайте оптическую силу линзы по формуле (2), используя расстояния f и d, и сравните полученный результат с величиной обратной фокусному расстоянию (тем самым проверьте справедливость формулы тонкой линзы). Сделайте соответствующие выводы.
2. Рассчитайте увеличение Г, даваемое линзой по формуле (3) двумя способами и сделайте соответствующие выводы
3. Рассчитайте радиус кривизны линзы по формуле (4).
4. Погрешности в измерениях оптической силы и радиуса кривизны линзы определите как при многократных измерениях. Таблица 1
Контрольные вопросы: 1. Что такое линза? Какие бывают линзы, от чего это зависит? Какая линза называется тонкой?
2. Что такое фокус линзы, оптическая сила линзы, радиус кривизны линзы?
3. Запишите формулу тонкой линзы, объясните правила знаков в этой формуле.
4. Объясните, почему увеличение, даваемое линзой можно рассчитывать как через h и H, так и через f и d.
5. Изобразите продолжения пяти лучей попавших на собирающую линзу
6. Изобразите продолжения пяти лучей попавших на рассеивающую линзу
7. Охарактеризуйте изображение предмета даваемого собирающей или рассеивающей линзой в зависимости от положения предмета (для ответа можно пользоваться геометрическими построениями). 1) Линза собирающая, предмет между линзой и F изображение:______________________________ 1) Линза собирающая, предмет между F и 2F изображение:______________________________ 1) Линза собирающая, предмет за 2F изображение:______________________________ 1) Линза собирающая, предмет в 2F изображение:______________________________ 1) Линза собирающая, предмет в F изображение:______________________________ 1) Линза рассеивающая, предмет за 2F изображение:______________________________ 1) Линза рассеивающая, предмет в F изображение:______________________________
Выводы: Лабораторная работа №4 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 (1),
(1), где
где 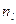 - абсолютный показатель преломления материала линзы;
- абсолютный показатель преломления материала линзы;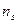 - абсолютный показатель преломления среды, в которой находится линза;
- абсолютный показатель преломления среды, в которой находится линза; ставится знак плюс, если же поверхность вогнутая, то минус).
ставится знак плюс, если же поверхность вогнутая, то минус). (2),
(2),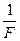 ставится если линза собирающая, а минус если рассеивающая. Перед
ставится если линза собирающая, а минус если рассеивающая. Перед  ставится знак плюс, если изображение действительное и минус, если оно мнимое.
ставится знак плюс, если изображение действительное и минус, если оно мнимое. (3)
(3) (4)
(4) ) и находится в воздухе (
) и находится в воздухе ( 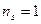 )
) , %
, %
 ,
м
,
м
 , %
, %

