
|
|
Краткие теоретические сведенияКолебательным контуром называется устройство, состоящее из последовательно соединенных конденсатора, катушки индуктивности и резистора (наличие резистора возможно, но не обязательно). Основной характеристикой конденсатора является его емкость C. В идеальном конденсаторе нет диссипативных потерь энергии. Его сопротивление чисто реактивное. В реальных конденсаторах диэлектрик, заполняющий пространство между обкладками, может иметь небольшую электропроводность, и поэтому возможны некоторые потери энергии на выделение Джоулева тепла. Кроме того, при электрических колебаниях периодически происходит переполяризация диэлектрика, на которую также затрачивается некоторое количество энергии. В некоторых случаях приходится учитывать также тот факт, что кроме емкости C конденсатор, как и любой проводник, может иметь небольшое значение индуктивности L, величина которой зависит от конструкции конденсатора. Основной характеристикой катушки индуктивности является ее индуктивность L. Идеальная катушка, в которой нет потерь энергии, имеет чисто реактивное сопротивление. Однако, если в катушке применяется сердечник, то при колебаниях в контуре часть энергии теряется на перемагничивание сердечника. Часть энергии теряется также на нагревание проводника обмотки, имеющей конечное значение сопротивления. Большое влияние на реальное сопротивление катушки оказывают так называемые межвитковые емкости. Эти емкости имеют наименьшее значение в однослойных катушках с принудительным шагом (шаг спирали больше диаметра провода) и наибольшее в многослойных катушках с намоткой внавал. Резисторы, кроме активного сопротивления R , могут иметь некоторое значение индуктивности. В идеальном случае можно считать, что колебательный контур состоит из последовательно соединенных идеальных элементов L, R и C. Рассмотрим колебательный контур, состоящий из этих элементов. При наличии электромагнитных колебаний в контуре энергия магнитного поля сосредоточена в катушке и равна Если бы потерь энергии не было (при
Выражение (2) после взятия производной и учитывая определение силы тока Если ввести обозначения
Выражение (4) является стандартной формой записи дифференциального уравнения любого линейного осциллятора, совершающего свободные затухающие колебания. Решением уравнения (4) является функция где частота колебаний
В выражении (5) произведение Период свободных колебаний в контуре
При отсутствии потерь энергии (или когда амплитуды двух соседних, отличающихся на один период, колебаний почти одинаковы и потерями энергии за один период по сравнению с
Из выражения (7) следует, что с увеличением сопротивления
называется критическим. Решение дифференциального уравнения (4), представленное выражением (5) трудно проверить экспериментально, так как мы не располагаем прибором, позволяющим непосредственно измерять заряд конденсатора для каждого момента времени. Однако мы можем сравнительно легко измерить напряжение на конденсаторе. Напряжение на конденсаторе, имеющем емкость С
Для характеристики степени затухания колебаний колебательной системы кроме коэффициента затухания
Можно показать, что логарифмический декремент колебательного контура связан с параметрами контура соотношением Если затухание мало, то в соответствии с (8)

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 . Энергия электрического поля сосредоточена в конденсаторе и равна
. Энергия электрического поля сосредоточена в конденсаторе и равна  . Полная энергия электромагнитного поля в контуре равна
. Полная энергия электромагнитного поля в контуре равна  (1)
(1) ), то энергия была
), то энергия была  бы постоянной, а производная от этой энергии по времени равнялась нулю. Если сопротивление R отлично от нуля, то в резисторе выделяется Джоулево тепло, на что расходуется энергия электромагнитного поля. При этом, в соответствии с законом сохранения энергии, изменение энергии
бы постоянной, а производная от этой энергии по времени равнялась нулю. Если сопротивление R отлично от нуля, то в резисторе выделяется Джоулево тепло, на что расходуется энергия электромагнитного поля. При этом, в соответствии с законом сохранения энергии, изменение энергии 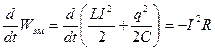 (2)
(2) можно привести к виду
можно привести к виду  (3)
(3) ;
;  , то получим уравнение
, то получим уравнение (4)
(4) , (5)
, (5) . Для колебательного контура
. Для колебательного контура (6)
(6) имеет смысл амплитуды, величина которой убывает со временем. Коэффициент
имеет смысл амплитуды, величина которой убывает со временем. Коэффициент 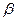 называется коэффициентом затухания. Чем больше коэффициент
называется коэффициентом затухания. Чем больше коэффициент 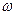 . В идеальном случае, когда потери отсутствуют и коэффициент
. В идеальном случае, когда потери отсутствуют и коэффициент 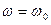 . Частоту
. Частоту  называют собственной частотой колебаний в колебательном контура.
называют собственной частотой колебаний в колебательном контура. (7)
(7) можно пренебречь)
можно пренебречь) (8)
(8) период
период  также увеличивается и при приближении к значению
также увеличивается и при приближении к значению  стремится к бесконечности. При значениях R, больших, чем
стремится к бесконечности. При значениях R, больших, чем  (9)
(9) (10)
(10)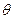 . Логарифмическим декрементом затухания называется натуральный логарифм отношения амплитуд, соответствующих моментам времени, различающимся на период, т.е.
. Логарифмическим декрементом затухания называется натуральный логарифм отношения амплитуд, соответствующих моментам времени, различающимся на период, т.е. (11)
(11) (12)
(12)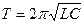 и
и (12а)
(12а)