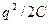|
|
Описание установки и метода измеренияСхема лабораторной установки показана на рисунке
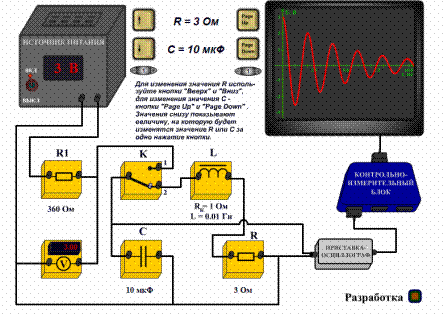 Колебательный контур состоит из катушки L, конденсатора С, резистора R. Колебательный контур подключен к источнику ЭДС через ключ K. В положении ключа 1 конденсатор заряжается, затем ключ переключают в положение 2, и в контуре совершаются свободные колебания. Колебательный контур состоит из катушки L, конденсатора С, резистора R. Колебательный контур подключен к источнику ЭДС через ключ K. В положении ключа 1 конденсатор заряжается, затем ключ переключают в положение 2, и в контуре совершаются свободные колебания.
Для того, чтобы измерить период собственных колебаний нужно воспользоваться шкалой времени с ценой деления k = 0,5 мс (измерив по этой шкале продолжительность промежутка времени между двумя соседними локальными максимумами (минимумами) или промежуток времени между двумя ближайшими точками пересечения осциллограммы временной оси находящимися в одинаковых фазах).
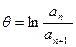 (13) (13)
Нетрудно доказать, что логарифмический декремент затухания можно найти по отношению любых двух амплитуд Точность измерения логарифмического декремента затухания зависит от точности измерения амплитуд по шкале прибора. При измерении амплитуд
Порядок выполнения работы: 1. Установить параметры колебательного контура (сопротивление R и электроёмкость С) в соответствии с вариантом:
2. Включить источник питания. 3. Зарядить конденсатор от источника постоянного напряжения, установив ключ К в положение 1. 4. Переключить ключ К в положение 2. 5. Наблюдать за изменением напряжения в колебательном контуре и зафиксировать три значения периода колебаний на трёх любых участках графика. Результаты измерений периода колебания занести в таблицу 1. 6. Измерить амплитуды Таблица 1.
Обработка результатов измерений: 1. По результатам эксперимента вычислить средние значения периода колебаний. 2. Логарифмический декремент затухания рассчитать по формуле (15). 3. Найти абсолютные и относительные погрешности периода и логарифмического декремента затухания как при многократных измерениях. Результаты вычислений внести в табл.1. 4. По данным выбранного варианта, используя значение электроемкости C и активного сопротивления R, индуктивности L (см. в данные установки)вычислить теоретические значения периода колебаний Tтеор, учитывая активное сопротивление катушки (формула (7)) и логарифмический декремент затухания qтеор (формула (12), при условии малости затухания формула (12а)). 5. Сравнить экспериментальные (взятые из таблицы 1) и теоретические значения периода колебаний и логарифмического декремента затухания, внеся данные в таблицу 2. Сделать соответствующие выводы. Таблица 2
Контрольные вопросы: 1. Какие колебания называются свободными?
2. Запишите дифференциальное уравнение, описывающее затухающие колебания в колебательном контуре, в чем его отличие от соответствующего ему уравнения незатухающих колебаний, вынужденных колебаний?
3. Перечислите основные параметры свободных затухающих колебаний (и их определения).
4. Как выглядит решение дифференциального уравнения для случая затухающих колебаний. Чему равны период колебаний Т и коэффициент затухания
5. Что такое логарифмический декремент затухания? Как он выражается через параметры контура? Соотношение между
6. Что такое критическое сопротивление? Его выражение через параметры контура.
Тесты 1. Формула периода колебаний контура без потерь энергии А. 2. Формула дифференциального уравнения колебания контура А.
3. Формула частоты колебаний контура с потерями А. 4. Критическое сопротивление контура А. 5.Логарифмический декремент связан с параметрами контура соотношением А. 6. С увеличением величины заряда конденсатора частота колебаний контура А. увеличивается В. уменьшается С. не изменяется
7. С увеличением величины сопротивления частота колебаний A. увеличивается В. уменьшается С. не изменяется.
8. Собственной частотой колебательного контура называют частоту, когда… А.
9. При наличии электромагнитных колебаний в контуре энергия магнитного поля сосредоточена в A. катушке и равна С. конденсаторе и равна
10. С увеличением индуктивности затухание в колебательном контуре А. увеличивается В. уменьшается С. не изменяется Выводы:
Лабораторная работа №3

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 Схема для определения логарифмического декремента затухания при помощи осциллографа представлена на рисунке 2. Зная цену деления шкалы напряжений (m=1В), измеряем амплитуду напряжения на конденсаторе для колебания под номером n, т.е.
Схема для определения логарифмического декремента затухания при помощи осциллографа представлена на рисунке 2. Зная цену деления шкалы напряжений (m=1В), измеряем амплитуду напряжения на конденсаторе для колебания под номером n, т.е. 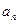 , а так же амплитуду напряжения следующего колебания, с номером
, а так же амплитуду напряжения следующего колебания, с номером  . Тогда логарифмический декремент затухания
. Тогда логарифмический декремент затухания 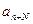 по формуле
по формуле 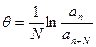 (14)
(14)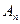 и
и  , как показано на рисунке 2. Можно доказать, что при этом
, как показано на рисунке 2. Можно доказать, что при этом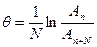 (15)
(15)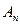 и
и  (записывая количество полных колебаний N) для трёх различных участков графика. Результаты измерения занести в таблицу 1.
(записывая количество полных колебаний N) для трёх различных участков графика. Результаты измерения занести в таблицу 1.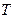 , с
, с
 ,с
,с
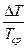 , %
, %
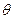

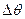
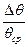 , %
, %
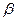 ? Как эти величины выражаются через параметры контура L, C и R ?
? Как эти величины выражаются через параметры контура L, C и R ?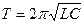 В.
В. 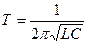 С.
С.  D.
D. 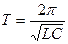
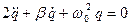 В.
В. 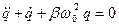 С.
С. 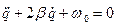 D.
D. 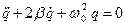
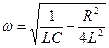 В.
В. 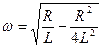 С.
С.  D.
D. 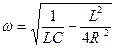
 В.
В. 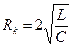 С.
С. 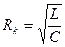 D.
D. 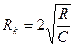
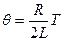 В.
В.  С.
С. 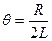 D.
D. 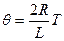
 B.
B. 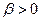 С.
С. 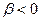
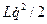 B. катушке и равна
B. катушке и равна