
|
|
Описание установки и метода измерения
математический маятник, длину которого можно регулировать, захватив мышью шарик и перемещая его вверх или вниз (или нажимая клавиши «Меньше» и «Больше»); таймер (секундомер) с точностью измерения времени до сотых долей секунды; специальный пусковой механизм, с клавишей «Отклонить», для того чтобы угол отклонения не устанавливался слишком большим (лишь при малых углах отклонения колебания реального маятника можно условно считать гармоническими). Для определения gпо формуле (9)необходимо измерить период колебаний маятника T и его длину l. Однако непосредственное измерение длины маятника в реальных условиях представляет собой сложную задачу, так как приходится определять центр тяжести, который при неоднородности материала шарика и неточности шаровой поверхности нелегко найти. В виртуальной работе устанавливается длина нити, а радиус шарика считается неизвестным, хотя в (9) l – расстояние от точки подвеса до центра тяжести шарика. Чтобы обойти эту трудность воспользуемся маятником переменной длины. Сначала с помощью секундомера измерим период колебаний маятника с длиной нити l1, а затем изменим длину и измерим период колебаний с длиной нити l2. Так как на основании (8)
Так как в (10) используется разность длин Порядок выполнения работы: 1. Установите длину нити математического маятника l1 (запишите эту длину в таблицу 1) в соответствии с вариантом:
2. Нажмите клавишу «Отклонить» и измерьте время нескольких (N=30) полных колебаний маятника. Остановите секундомер вручную, и запишите полученное время с точностью до сотых долей секунды в таблицу 1. 3. Не меняя длину нити, повторите пункт 2 ещё 4 раза. 4. Измените длину нити l не менее чем на 80 см и запишите длину l2 в таблицу 1. 5. Повторите пункт 2 с длиной l2 5 раз, записывая время в таблицу 1. Таблица 1
Обработка результатов измерений: 1. Средние значения всех величин считайте как среднее арифметическое. 2. Зная количество полных колебаний N, рассчитайте период колебаний по формуле 3. Погрешности времени и периода определите как при многократных измерениях. 4. Ускорение свободного падения рассчитайте по формуле (10), используя средние значения периодов. 5. Относительную погрешность измерения ускорения свободного падения dg рассчитайте по формуле
6. Абсолютную погрешность измерения ускорения свободного падения рассчитать по формуле
где dg должно быть выражено не в %. Контрольные вопросы: 1. Какие колебания называются свободными?
2. Что такое гармонический осциллятор? Перечислите основные характеристики колебаний гармонического осциллятора (дайте им определения)
3. Приведите примеры гармонических осцилляторов (кратко их опишите).
4. Как выглядит дифференциальное уравнение колебаний математического маятника и его решение? Что является колеблющейся величиной в этом случае?
5. Какие характеристики математического маятника нужно знать, чтобы можно было рассчитать ускорение свободного падения (по какой формуле это можно сделать)?
Тесты 1. Период колебаний математического маятника при покоящейся (или движущейся равномерно и прямолинейно) точке подвеса определяется по формуле А.
2. Период колебаний математического маятника в случае вертикального равнопеременного движения точки подвеса с ускорением направленным вверх определяется по формуле А.
3. Дифференциальное уравнение колебания математического маятника имеет вид А.
4. Ускорение свободного падения с помощью математического маятника можно рассчитать, зная А. длину нити и массу материальной точки В. частоту колебаний и длину нити С. частоту и период колебаний D. период колебаний и массу материальной точки
5. При колебаниях математического маятника гармонически колеблется А. угол отклонения В. угловая скорость С. угловое ускорение D. потенциальная энергия
6. При колебаниях математического маятника не колеблется А. угловое ускорение В. возвращающая сила С. полная механическая энергия D. кинетическая энергия
7. Чему равно ускорение свободного падения на планете X, если уравнение колебаний математического маятника длиной 2 метра на этой планете имеет вид А. 8. Если уравнение колебаний пружинного маятника имеет вид А. 9. Если уравнение колебаний пружинного маятника имеет вид А.
10. Если уравнение колебаний пружинного маятника имеет вид А.
Выводы:
Лабораторная работа №2 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
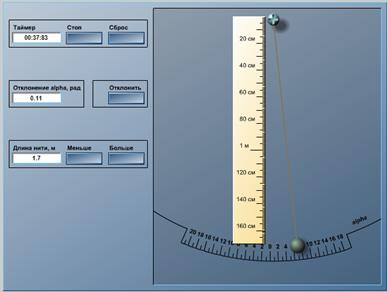 Виртуальная установка содержит:
Виртуальная установка содержит: , а
, а  , то
, то (10)
(10) , то неизвестный радиус шарика становится неважным, и по формуле (10) мы получим более точный результат для g, чем по формуле (9).
, то неизвестный радиус шарика становится неважным, и по формуле (10) мы получим более точный результат для g, чем по формуле (9). .
.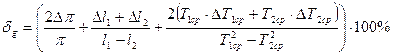
 ,
, В.
В.  С.
С.  D.
D. 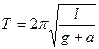
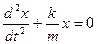 В.
В.  С.
С.  D.
D. 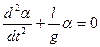
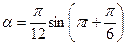
 В.
В.  С.
С.  D.
D. 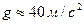
 , то фаза колебаний в момент времени t равна
, то фаза колебаний в момент времени t равна В.
В.  С.
С.  D.
D. 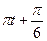
 В.
В.  С.
С. 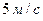 D.
D. 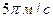
 В.
В.  С.
С.  D.
D. 