
|
|
Определение коэффициентов местных сопротивленийЗадание: 1. Определить экспериментально коэффициент местного сопротивления для случая внезапного расширения потока. 2. Рассчитать для этого же случая значение коэффициента местного сопротивления по аналитической зависимости.
Общие сведения
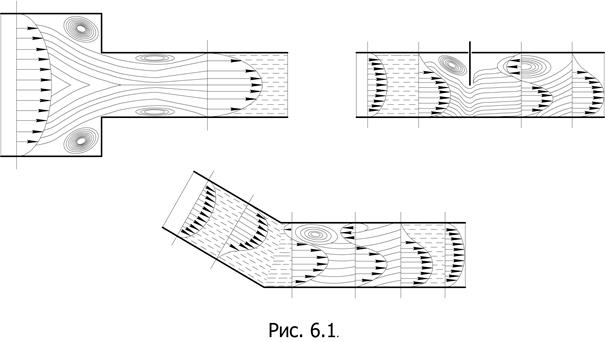
Местные гидравлические сопротивления – короткие участки трубопроводов или каналов, в которых происходит изменение скоростей потока и возникают вихревые зоны. Местные сопротивления бывают трех видов: – обусловленные изменением сечения потока (внезапное и плавное сужение и расширение); – возникающие в результате изменения направления движения потока (повороты на различные углы); – возникающие при прохождении жидкости через запорные регулирующие и другие устройства (краны, вентили, клапаны и т.д.). см. рис. 6.1.
На рис. 6.1. показаны зафиксированные в опытах картины течений в области различных местных сопротивлений. Во всех случаях можно видеть образование отрывов и водоворотных (вихревых) зон, которые характеризуются возвратным течением. Благодаря этим течениям потери энергии в местных сопротивлениях намного превосходят потери по длине на участке той же протяженности, что и местное сопротивление. Потери энергии в местных сопротивлениях называются местными потерями напора и определяются в долях кинетической энергии по формуле Вейсбаха: h где
Величина В связи со сложностью структуры потока в местных сопротивлениях, только в отдельных случаях (например, внезапное расширение потока) hм, и zм, определяются теоретически. В преобладающем большинстве случаев коэффициенты zм, найдены экспериментально и имеются в справочной литературе. Исследованиями установлено, что zм зависит от Re лишь при ламинарном режиме движения. В турбулентных потоках при достаточно больших Re влияние последних на величину коэффициентов zмнезначи-тельно, поэтому их считают зависящими только от вида и конструк-тивного исполнения местного сопротивления. Потери напора при внезапном расширении находят по формуле Борда: h где Таким образом, потеря напора при внезапном расширении трубопровода ровна скоростному напору от потерянной скорости. Коэффициент сопротивления в формуле Вейсбаха (6.1.) определяя-ется выражениями:
где w1; w2 – площади поперечных сечений до и после внезапного расширения Суммирование потерь энергии производится в соответствии с принципом наложения потерь, согласно которому полные потери давления на рассматриваемом участке представляют собой арифметическую сумму потерь напора, вызванную каждым сопротив-лением в отдельности.
где
Где Необходимо помнить, что принцип наложения потерь напора применим, если местные сопротивления находятся друг от друга на расстоянии Для коротких трубопроводов принцип наложения потерь вносит неточность, т.к. не учитывает влияние одного местного сопротивления на другое, с ним соседнее.
Описание лабораторной установки
Работа выполняется на той же лабораторной установке, что и предыдущая с той лишь разницей, что пьезометры подключаются к одному из имеющихся местных сопротивлений. В данном случае сопротивлением будет внезапное расширения потока. Диаметры трубо-провода до и после расширения равны 10 мм и 20 мм соответственно.
Порядок выполнения работы
Измерить диаметр трубопровода до и после местного сопротивления. Краном 9 установить расход воды и определить среднюю, скорость течения до и после расширения. Измерить потери напора в местном сопротивлении по показаниям пьезометров 7. Определить абсолютные погрешности измерений: объема – равную половине наименьшей цены деления мерного бака Определить коэффициент местного сопротивления внезапного расширения по результатам измерения, используя формулу (6.1.) Определить коэффициенты местных сопротивлений по расчетным формулам (6.3) и (6.4).
Обработка опытных данных
При обработке опытных данных заполняют табл. 6.1. Определить расход воды: Q= Определить средние скорости течения до и после внезапного расширения.
где d1 и d2 – диаметры трубопровода до и после расширения.
Определить расчетные коэффициенты местных сопротивлений по формулам (6.3) и (6.4). Определить наименьшую относительную погрешность измерения скорости
где Таблица 6.1
Контрольные вопросы
1. Дать определение и перечислить виды местных сопротивлений. 2. Объяснить физическую сущность потерь напора в местных сопротивлениях. 3. Какие факторы влияют на величину zм при различных режимах движения жидкости? 4. Методика экспериментального определения zм. 5. Как определить коэффициент сопротивления системы из нескольких местных сопротивлений? 6. Оценить погрешность измерений и достоверность результатов.
Лабораторная работа №7

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
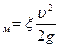 ,
,  (6.1)
(6.1) – средняя скорость в сечении трубопровода или канала (обычно за местным сопротивлением);
– средняя скорость в сечении трубопровода или канала (обычно за местным сопротивлением); – коэффициент местного сопротивления.
– коэффициент местного сопротивления.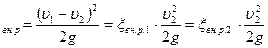 (6.2)
(6.2) (6.3)
(6.3) (6.4)
(6.4) , (6.5)
, (6.5) . (6.6)
. (6.6) – коэффициент местного сопротивления каждого из сопротивлений системы.
– коэффициент местного сопротивления каждого из сопротивлений системы. ≥ (20.. .50)d, где d – диаметр трубопровода.
≥ (20.. .50)d, где d – диаметр трубопровода.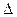 W; времени – равна наименьшей цене деления секундомера –
W; времени – равна наименьшей цене деления секундомера – 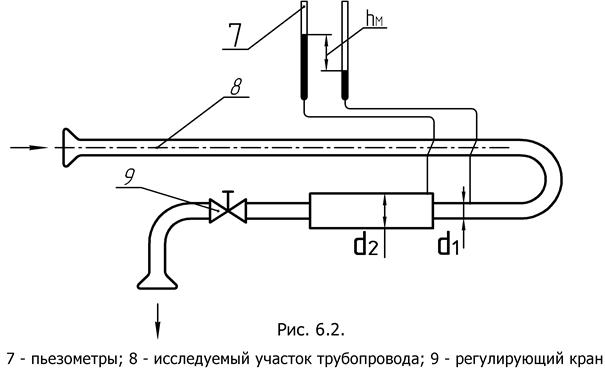
 ,
,  /с.
/с. ,
,  ,
, 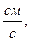
 Определить измеренный коэффициент местного сопротивления из формулы (6.1) для
Определить измеренный коэффициент местного сопротивления из формулы (6.1) для  и
и  .
. и коэффициента местного сопротивления d
и коэффициента местного сопротивления d  .
.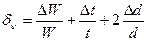

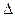 W,
W, 