
|
|
Экспериментальная проверка уравненияД. Бернулли Задание: 1. По данным замеров построить линию полного давления и пьезометрическую линию для установившегося расхода в трубопроводе переменного сечения. 2. Провести наблюдение за изменением скоростного напора при изменении расхода жидкости в трубопроводе. 3. Определить средние скорости движения воды в сечениях трубопровода, расход и потери напора между сечениями.
Общие сведения
Уравнение Д. Бернулли является основным уравнением гидродинамики и представляет аналитическое выражение закона сохранения энергии, устанавливая зависимость между средней скоростью и гидродинамическим давлением жидкости. Для потока реальной жидкости при двух сечениях потока, находящихся на расстоянии друг от друга, уравнение имеет вид:
Z где Z1, Z2 – геометрическая высота или геометрический напор, т.е. расстояние от произвольной горизонтальной плоскости сравнения 0-0 до рассматриваемой точки в сечении (рис.4.1);
hw – потери напора при движении жидкости на участке между сечениями. Все слагаемые уравнения (4.1) имеют размерность длины, следовательно уравнение можно представить геометрически в виде отрезков или как сумму трех высот (рис.4.1).
Отложив в масштабе величины Z1 , Z2 , Z3 и соединив концы отрезков получим ось трубопровода. Величину ir называют геометри-ческим уклоном между сечениями: В общем случае геометрический уклон может быть как положительным так и отрицательным. Отложив на оси трубопровода вверх величины P/
Пьезометрический уклон для двух сечений определяется зависимостью:
Пьезометрический уклон также как и гидравлический может быть знакопеременным. Отложив вверх от пьезометрического скоростного напора и соединив полученные точки, получим уклон, который называется гидравлическим или линию полной удельной энергии потока. Гидравлический уклон между сечениями I–I и II–II записывается в виде:
I или I= Напорная линия по длине потока всегда понижается, так как часть напора затрачивается на преодоление сопротивления. Иными словами I всегда положителен. Сумма трех членов уравнения называется гидродинамическим напором и обозначается "Н". Для двух сечений запишем:
H (4.6) H
С энергетической точки зрения, уравнение (4.6) выражает сумму трех удельных энергий потока реальной жидкости в сечениях I-I и Z+
Z – удельная потенциальная энергия положения
Лабораторная установка
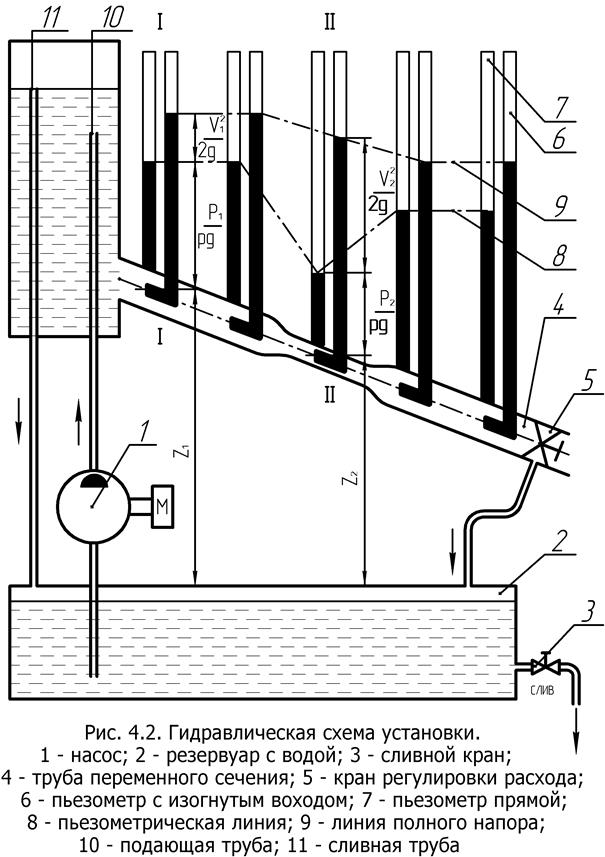
Схема экспериментальной установки представлена на рис. 4.2. установка состоит из бака - 2, служащего одновременно основанием установки, напорного резервуара - 12 с переливной трубой - 11 и трубой переменного сечения - 4, центробежного насоса 1 - и пьезометров - 6, 7. Основным элементом установки является труба переменного по длине сечения, закрепленная наклонно. Для измерений труба оборудована пьезометрами и трубками для измерения полного напора (трубка Пито). Изменение расхода жидкости в трубе осуществляется краном - 5.
Порядок проведения опытов
Перед проведением опытов закрыть кран – 5, включить насос – 1 и заполнить резервуар 12 водой. После заполнения резервуара, приоткрывая регулировочный кран 5 установить желательный режим опыта. Постоянство напора, т. е. уровень жидкости в резервуаре, должен обеспечиваться подачей насоса и переливной трубкой 11. Режимы опытов рекомендуется выбирать такими, чтобы скоростной напор в наиболее узком сечении трубы переменного сечения находился в пределах 50–200 мм. При каждом режиме фиксируются положения линии гидродинамического напора и пьезометрической линии по уровню воды в стеклянных трубках. Изменение режима опыта осуществить дважды, т.е. измерение расхода и скорости движения воды в трубе переменного сечения осуществить три раза. При каждом произвести сравнение изменения положения линии пьезометрического и гидродинамического напора. Результаты измерения занести в табл. 4.1. Для одного из режимов построить линию полного давления (график подобный рис. 4.1.)
Обработка опытных данных
При обработке опытных данных заполняют таблицу 4.2. Для каждого опыта определяют среднюю скорость воды в сечениях трубопровода по величине измеренного скоростного напора Hc: Hс Для каждого опыта определяют расход: Q = где S - площадь соответствующего поперечного сечения трубопровода, м2.
Потери напора между выбранными сечениями трубопровода определяют как разность между гидродинамическими напорами в сечениях. Например: h h h Исходные данные. Размеры сечения трубопровода: наибольшая ширина – 10 мм, высота – 30 мм; наименьшая ширина – 10 мм, высота – 10 мм. Геометрические высоты: Z1 = 35 см, Z2 = 33 см, Z3 = 31,5 см. Расстояние между сечениями: L12 = L23 = 31 см.
Измеренные величины Таблица 4.1
Расчетные величины Таблица 4.2
Контрольные вопросы
1. Устройство лабораторного стенда. 2. Физический смысл геометрического, пьезометрического, скорост-ного и полного напоров, методика их экспериментального определения. 3. Что такое гидродинамический напор? 4. Уравнение Бернулли, назначение и физический смысл. 5. Чем вызваны потери энергии при движении вязкой жидкости по трубопроводу? 6. Как определяется средняя скорость потока? 7. Каково назначение и физический смысл коэффициента a? 8. Дать понятие гидравлического, пьезометрического и геометри-ческого уклонов. Лабораторная работа №5

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
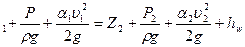 , (4.1)
, (4.1)
 – пьезометрическая высота или пьезометрический напор, соответствующий манометрическому давлению;
– пьезометрическая высота или пьезометрический напор, соответствующий манометрическому давлению;

 – скоростной напор в сечениях;
– скоростной напор в сечениях; 1;
1; 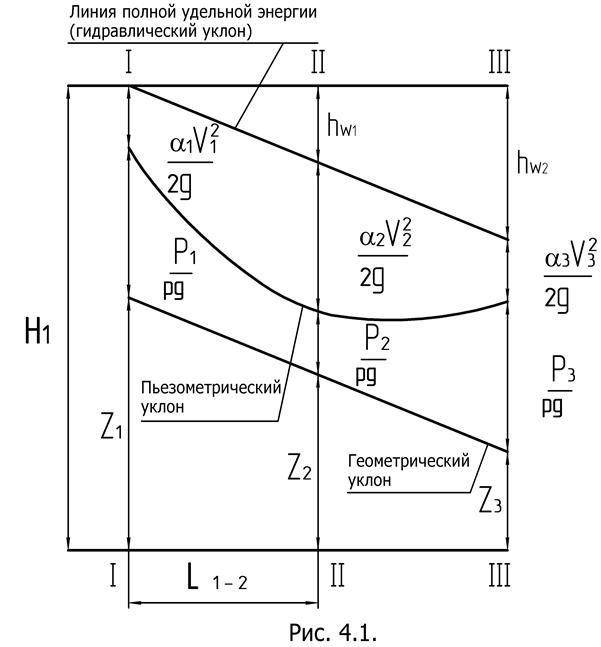
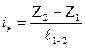 (4.2)
(4.2)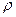 g и соединив концы отрезков, получим пьезометрическую линию.
g и соединив концы отрезков, получим пьезометрическую линию.
 (4.3)
(4.3) (4.4)
(4.4) (4.5)
(4.5)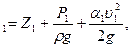
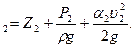
 -
-  – удельная потенциальная энергия;
– удельная потенциальная энергия; – удельная кинетическая энергия;
– удельная кинетическая энергия; – удельная потенциальная энергия давления.
– удельная потенциальная энергия давления. м отсюда
м отсюда 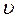 =
= 
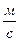
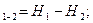
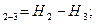
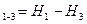 .
.