
|
|
Определение режима движения жидкости
Задание: установить и визуально пронаблюдать ламинарный и турбулентный режим движения жидкости. Определить, установленные произвольно, режимы движения жидкости по критерию Рейнольдса.
Общие сведения
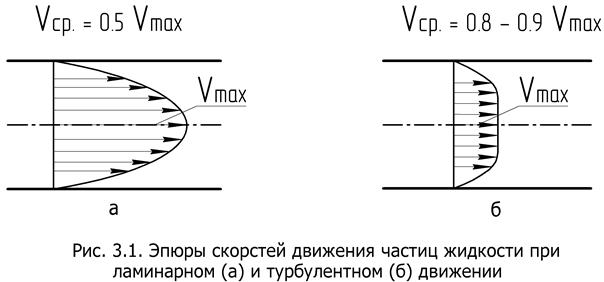
При течении жидкости характер или режим движения ее может быть ламинарным (слоистым) или турбулентным (беспорядочным). В случае ламинарного режима отдельные частицы жидкости движутся по траекториям, параллельным стенкам, без перемешивания. Струи по сечению потока обладают разными скоростями, но скорость каждой постоянна и направлена вдоль оси потока. При ламинарном движении скорость частиц по сечению трубы изменяется по параболе от нуля у стенок до максимума на ее оси (рис. 3. 1,а) Средняя скорость жидкости при этом равна половине максимальной.
При турбулентном режиме частицы жидкости движутся по пересекающимся траекториям. Здесь имеет место перемешивание жидкости. В каждой точке потока происходят быстрые изменения скорости по величине и направлению так называемые пульсации скорости. В турбулентном потоке изменение скорости в поперечном сечении идет по более пологой кривой и средняя скорость составляет 0,8...0,9 от максимальной (рис. 3.1 б). Впервые существование двух принципиально разных режимов движения жидкости было открыто немецким гидротехником Г. Хагеном в 1839 г. Д.И Менделеев в своем труде "Сопротивление жидкости и о воздухоплавании" в 1880 году отметил существование двух режимов движения жидкости. Однако специальные исследования ламинарного и турбулентного режимов движения были проведены в 1883 г. английским физиком О. Рейнольдсом, который экспериментально доказал существование двух режимов движения жидкости, и получил математическую зависимость количественно определяющую характер движения потока. Эта зависимость получила название критерий (число) Рейнольдса (Re). Для круглой трубы критерий Рейнольдса имеет вид:
где υ – средняя скорость потока, м/с;
m – динамический коэффициент вязкости, Н∙с/м2;
d – диаметр трубы, м. Установлено, что для ламинарного режима числовые значения всегда меньше, а для турбулентного всегда больше некоторого определенного критического значения. Например, для прямых круглых труб критическое значение числа Рейнольдса Reкр = 2320. Приведенное критическое значение является условной величиной, так как обнаружить четкую границу перехода от ламинарного режима к турбулентному затруднительно. В действительности обычно наблюдается так называемая переходная область исчезновения ламинарного режима и установления турбулентного режима движения. Числовые значения Re для переходной области находятся в пределах 2320... 10000. При значении Re больше 10000 режим движения потока становится устойчивым турбулентным. Для изогнутых труб критическое значение Re в зависимости от кривизны может достигать значений 7000...8000. При определении режима движения в трубах некруглого селения и при безнапорном движении жидкости в круглых трубах и каналах любой формы критерий Рейнольдса записывается в виде:
где R - гидравлический радиус, равный отношению площади живого сечения к смоченному периметру : R=S/c c- смоченный периметр - это линия соприкосновения потока с твердыми стенками трубы или канала. Гидравлический радиус для круглой трубы, работающей полным сечением, равен половине геометрического радиуса R= r/2 = d/4. Критическое значение числа Рейнольдса полученное по формуле (3.2) будет в четыре раза меньше, т.е. Re= 580.
Описание лабораторной установки
Гидравлическая схема лабораторной установки показана на рисунке 3.2. Подача воды в установку производится из водопровода, причем расход регулируется вентилем 1. Постоянный уровень (напор) в расходном баке 7 поддерживается с помощью перелива 2. Над расходным баком установлен бачок с подкрашивающей жидкостью 3, из которого она может поступать по капилляру 5 в стеклянную трубку 8. Расход подкрашивающей жидкости регулируется вентилем 4. Из расходного бака вода, при постоянном напоре, поступает в стеклянную трубку 8, куда из капилляра 5 поступает подкрашивающая жидкость. Скорость движения воды в стеклянной трубке 8 регулируется вентилем 10. Расход воды определяется мерным баком 9, имеющим водомерное стекло со шкалой
Порядок проведения работы
Работу начинают с заполнения установки водой при открытым вентиле 1 и закрытых 4,10. Установку можно считать заполненной когда вода начнет переливаться по трубе 2.
Вентилем 10 устанавливают минимальную скорость воды в стеклянной трубе и плавно открывают вентиль 4. Регулируя степень открытия вентиля 4, добиваются четкого очертания струйки подкрашенной жидкости. Наличие резко выделяющейся, четко очерченной неизломанной подкрашенной струйки указывает на существование ламинарного режима. При установившемся режиме движения измеряют расход жидкости Q, м3/с, мерным баком 9. Для этого закрывают вентиль 11, измеряют время прохождения уровня жидкости между двумя делениями шкалы водомерного стекла. Увеличивая степень открытия вентиля 10 и отрегулировав подачу подкрашивающей жидкости вентилем 4, устанавливают другие режимы движения воды в стеклянной трубке и делают соответствующие замеры. Таких опытов проводят несколько – 4,5, закончив их при развитом турбулентном режиме движения. Этому режиму соответствует интенсивное перемешивание струйки подкрашивающей жидкости на выходе из капилляра 5.
Обработка опытных данных
После проведения всех измерений проводят обработку полученных результатов. По измеренному объему мерного бака W, времени его заполнения t определяют расход воды: Q= Определяют среднюю скорость движения воды в стеклянной трубке: υ= где d- внутренний диаметр стеклянной трубки, м; S – площадь поперечного сечения, Значение критерия Рейнольдса определяют по формуле 3.1. Сравнивая полученные значения Re с критическими делают вывод о режиме движения жидкости в стеклянной трубе и сопоставляют с визуальными наблюдениями . Результаты наблюдения, опытные и расчетные данные заносятся в табл. 3.1. Таблица 3.1.
Контрольные вопросы
1. В чем отличие турбулентного течения от ламинарного? 2. Как распределяются скорости по сечению цилиндрической трубы при ламинарном и турбулентном движении жидкости? 3. Дать определение гидравлического радиуса. Дать понятие критической скорости. 4. Как определить критическую скорость? 5. Как рассчитать режим движения жидкости при движении ее в цилиндрической трубе и в русле произвольной формы?
Лабораторная работа №4

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|

 ,(3.1)
,(3.1) – плотность жидкости, кг/м3;
– плотность жидкости, кг/м3; – кинематический коэффициент вязкости, м/с;
– кинематический коэффициент вязкости, м/с;
 (3.2)
(3.2)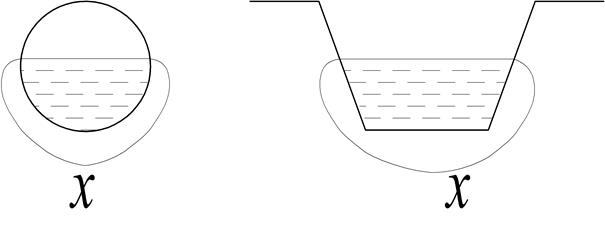

 ,
,  .
. ,
, 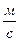 ,
, , м/с
, м/с