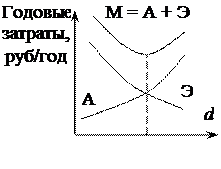|
|
Гидравлический расчет трубопроводовПлан
1.Сопротивление трения в гладких и шероховатых трубах. 2.Местные сопротивления. 3.Гидравлический расчет трубопроводов. 4.Понятие в технико-экономическом расчете трубопроводов.
1. Определение потерь напора hп необходимо для расчета затрат энергии для перемещения жидкости (с помощью насосов, компрессоров). Потери напора в трубопроводе расходуется на преодоление 1)путевых (линейных) сопротивлений (сопротивление трения) и 2)местных сопротивлений: hп = hтр + hмс. В общем случае путевые сопротивления зависят от режима течения жидкости и от шероховатости стенок труб. Для определения потерь напора на трение при равномерном движении жидкости в круглых трубах применяют формулу Дарси-Вейсбаха: λ показывает, какая доля динамического напора теряется на участке, равном диаметру трубы. Для некруглых труб в уравнении Дарси-Вейсбаха вместо диаметра d подставляют эквивалентный диаметр dэ. Зависимость
ε1 > ε2 > ε3 (относительная шероховатость). На графике Никурадзе можно выделить пять зон: 1) ламинарный режим (Re ≤ 2320) ( 2) переходная из ламинарного в турбулентный (Re=2320-3000); 3) область «гидравлически гладких» труб при турбулентном режиме: 4) область шероховатых труб (доквадратичная область «смешанного трения») при турбулентном режиме: 5) область «вполне шероховатых труб» (квадратичная или автомодельная область) при турбулентном режиме: Пока выступы шероховатости полностью погружены в ламинарный пограничный слой (∆ < δ), жидкость плавно обтекает эти выступы и влиянием шероховатости на величину λ можно пренебречь. В этом случае коэффициент λ зависит только от числа Re и определяется как для гидравлически гладких труб. (1 – 3-я зоны). С увеличением Re толщина слоя δ уменьшается. При ∆ ≥ δ ламинарное течение нарушается и λ начинает зависеть от шероховатости (4-ая зона), хотя еще и продолжает зависеть от Re. Если число Re очень велико и ∆ >> δ, то λ зависит только от шероховатости (5-ая зона). В практических расчетах для определения λ используются следующие формулы. 1-ая зона – ламинарный режим:
2-ая зона. Поток является неустойчивым, т.к. небольшое изменение Re приводит к сильному изменению сопротивления. Нерасчетная область. 3-я зона – гидравлически гладкие трубы.
4-ая зона – частично шероховатые трубы.
5-ая зона – шероховатые трубы.
или Все эти формулы справедливы для изотермических условий (T = const). При переменной температуре в эти формулы вводятся поправочные множители (т.к. μ = f(Т)). По опытным данным, для новых стальных труб ∆ ≈ 0,05 – 0,1 мм; для стальных труб после некоторой эксплуатации ∆ ≈ 0,1 – 0,2 мм; для старых чугунных и стальных труб ∆ ≈ 0,5 – 2 мм.
2. В местных сопротивлениях средняя скорость потока изменяется по величине, по направлению или одновременно по величине и направлению. К местным сопротивлениям относятся внезапные сужения и расширения труб, краны, вентили, тройники, вход в трубу, выход из трубы и т.д.
В местных сопротивлениях происходит дополнительная потеря энергии, кроме потерь на трение. Потеря энергии здесь вызывается ударом потока (аналогично удару твердого тела), который ведет к завихрениям жидкости. В практических расчетах местные потери определяют по формуле:
Т.о., потеря напора в местном сопротивлении пропорциональна скоростному напору. Для различных местных сопротивлений
Суммарно, для всех местных сопротивлений трубопровода Коэффициент местного сопротивления ξм.с. показывает, какая часть динамического напора теряется на данном местном сопротивлении. Коэффициенты местных сопротивлений определяют экспериментально. Их средние значения приводятся в справочниках.
3. При гидравлическом расчете трубопроводов путевые и местные сопротивления определяются независимо друг т друга и складываются. Полученная сумма является гидравлическим сопротивлением всей системы. Введем обозначение: Тогда hп = hтр + hмс = Данное правило расчета называется принципом наложения гидравлических потерь. По этому принципу: Т.о., потеря напора определяется по уравнению: или Величина hп выражается в метрах столба жидкости и не зависит от природы жидкости, а величина Иногда потерю напора в местном сопроивлении приравнивают потерям напора на трение в гипотетически прямой трубе эквивалентной длины lэкв. Длина участка прямой трубы, гидравлическое сопротивление которого равно потере напора в данном местном сопротивлении, называется эквивалентной длиной lэ этого местного сопротивления. Применяют формулу: lэкв =nd, где d – диаметр трубы; n – опытный коэффициент (приводится в справочниках). В этом случае общие потери напора:
Введем обозначение: Тогда При перекачивании жидкости по трубе, кроме гидравлического сопротивления сети, необходимо преодолевать статический напор Нст., который не зависит от расхода. Он состоит из высоты h подъема жидкости с уровня z1 на z2 (h = z2 - z1 ) и напора, соответствующего противодавлению в сети рк – р0. Где рк и р0 – давление в конце и в начале трубопровода. Т.о., полный напор для перекачивания жидкости:
График
4. Правильный выбор диаметра трубопровода важен потому, что сооружение и эксплуатация их обходятся дорого. При заданной производительности d трубопровода может быть определен из уравнения расхода: Большим диаметрам соответствуют малые скорости ω и малые потери напора hп, и перекачивание жидкости малы. Но при этом высоки капитальные и эксплуатационные затраты. Оптимальный диаметр трубопровода обеспечивает минимум эксплуатационных затрат. Пусть М – суммарные эксплуатационные затраты (руб/год). А – расходы на амортизацию и ремонт (руб/год). Э – затраты энергии на перекачивание по данному трубопроводу (руб/год).
dопт. соответствует минимуму на кривой М = А + Э. Для перекачивания жидкостей рекомендуются скорости 0,5 ÷ 2 м/сек, для газов – 15 ÷ 25 м/сек. При малых расходах и больших гидравлических сопротивлениях нужно брать небольшие скорости.

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
 , где l,d – длина и диаметр трубы; ω – средняя скорость потока; λ –коэффициент гидравлического трения, или коэффициент путевых сопротивлений.
, где l,d – длина и диаметр трубы; ω – средняя скорость потока; λ –коэффициент гидравлического трения, или коэффициент путевых сопротивлений. для труб с искусственной однородной шероховатостью (наклеивались зерны песка на внутреннюю поверхность труб) исследовал Никурадзе в 1932 г. Никурадзе получил график:
для труб с искусственной однородной шероховатостью (наклеивались зерны песка на внутреннюю поверхность труб) исследовал Никурадзе в 1932 г. Никурадзе получил график:
 ) - прямая I;
) - прямая I; .
. ;
;  ; кривые СiДi/
; кривые СiДi/ ;
;  . Горизонтальные прямые – вправо от точек Дi.
. Горизонтальные прямые – вправо от точек Дi. – формула Пуазейля.
– формула Пуазейля. – формула Блазиуса.
– формула Блазиуса. – формула Альштуля.
– формула Альштуля. – формула Прандля-Никурадзе.
– формула Прандля-Никурадзе. – формула Шифринсона.
– формула Шифринсона.
 ; где ω – средняя скорость потока в сечении за местным сопротивлением; ξм.с. – коэффициент местного сопротивления.
; где ω – средняя скорость потока в сечении за местным сопротивлением; ξм.с. – коэффициент местного сопротивления. .
. .
. , где ξтр. – коэффициент сопротивления трения.
, где ξтр. – коэффициент сопротивления трения. , где ∑ξ – сумма коэффициентов сопротивления трения и местных сопротивлений.
, где ∑ξ – сумма коэффициентов сопротивления трения и местных сопротивлений.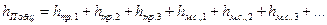
 .
. , т.к.
, т.к.  .
. зависит от плотности.
зависит от плотности. .
. , где ξ0 – общий коэффициент гидравлического сопротивления системы.
, где ξ0 – общий коэффициент гидравлического сопротивления системы. т.к.
т.к.  , где V – объемный расход; S – площадь сечения, то
, где V – объемный расход; S – площадь сечения, то  , где
, где  ; К характеризует гидравлическое сопротивление сети.
; К характеризует гидравлическое сопротивление сети. , где
, где  .
.
 также называется характеристикой сети. К2 > К1, т.е. гидравлическое сопротивление второй сети больше, чем первой. Характеристика сети – восходящая парабола.
также называется характеристикой сети. К2 > К1, т.е. гидравлическое сопротивление второй сети больше, чем первой. Характеристика сети – восходящая парабола. . Откуда
. Откуда  , где
, где  – объемный расход жидкости (м3/сек).
– объемный расход жидкости (м3/сек).