
|
|
Явления переноса и уравнение балансаПроведение ХТП связано с переносом субстанции – импульса (количества движения), теплоты и массы (вещества). Балансовые уравнения математически выражают законы сохранения субстанции. Цель составления баланса: 1) нахождение связи между элементами баланса; 2) определение неизвестного элемента баланса; 3) проверка сходимости баланса. Для составления баланса необходимо 1)выделить пространственный контур (контрольный объем); 2) установить временной интервал. Пространственный контур может охватывать несколько аппаратов, один аппарат, часть аппарата или бесконечно малый объем аппарата. В качестве временного интервала для периодических процессов обычно выбирают бесконечно малый промежуток времени Материальный баланс может быть частный (для одного компонента) и общий (для всех веществ в потоке). Пусть Пр – приход субстанции в контур; УХ- уход субстанции из контура; Ис Ст – источники и стоки субстанции внутри контура; Нак и Рез – накопление субстанции в контуре за данный временной интервал или результат процесса. Например, источником может быть образование вещества или выделение теплоты смешения внутри контура, а стоком – исчезновение (полное или частичное) вещества или поглощение теплоты при смешении компонентов. Источники и стоки отмечены на схеме крестиками или точками в маленьких кружочках.
Накопление – это разность между конечным и начальным количеством субстанции. Пусть масса субстанции М. В стационарном процессе Нак=МК-МН=0, т.е. накопление субстанции внутри контура К не происходит. В периодическом процессе для элементарного промежутка времени Баланс импульса обычно сводится к балансу к балансу взаимодействующих сил. При этом внешние массовые силы (например, силу гравитации) относят к источникам или стокам импульса внутри контура. В этом случае применяют термин Результат (Рез) – изменение ситуации под действием равнодействующей всех сил, а не Накопление (Нак). Запишем основное балансовое соотношение (ОБС): ΣПр-ΣУх+ΣИс-ΣСт = Нак (Рез) Для стационарного непрерывного процесса при отсутствии Источников и Стоков ОБС упрощается: ΣПр = ΣУх
Аналогия процессов переноса субстанции А) Законы молекулярного переноса Различают два типа механизма переноса субстанции через поверхность S: 1 молекулярный – за счет хаотического теплового движения молекул; 2)конвективный (макроскопический) – макрообъемами системы (струйками). В ламинарном потоке и неподвижной среде определяющую роль играет молекулярный перенос. Последний обусловлен стремлением системы к термодинамическому равновесию, т.е. к усреднению потенциала в данном объеме. При переносе импульса потенциалом переноса может служить скорость ω или импульс единицы объема жидкости: [ω·ρ]=[кг·м/м3·с]. При переносе теплоты – температура или энтальпия единицы объема жидкости: [cp·ρ·t]=[Дж/м3], где cp – удельная массовая теплоемкость при постоянном давлении [cp]= [Дж/кг·К]. Изоповерхность – поверхность с постоянным значением потенциала переноса, например, изотермическая поверхность. Удельный поток субстанции q (приходящий на 1 м2 изоповерхности в 1с и нормальный к этой поверхности) пропорционален градиенту потенциала переноса. Градиент потенциала – рост потенциала на единицу длины по нормали к изоповерхности.
Молекулярный перенос импульса описывается законом внутреннего трения Ньютона:
Направления потока импульса и градиента локальной скорости противоположны, поэтому в (А) знак «-». Физический смысл μ: сила, действующая между двумя параллельными площадками в 1 м2 в жидкости, расстояние между которыми 1м, а разность скоростей площадок 1м/с. Продольное касательное напряжение внутреннего трения τТ имеет размерность Н/м2, т.е. Па. Уравнение (А) можно записать ωρ:
[ν]= [м2/с]. Молекулярный перенос теплоты подчиняется закону Фурье:
[qMt]= [Вт/м2]. Физический смысл коэффициента теплопроводности λ: количество теплоты, проходящей в 1с. Между двумя площадками в 1м2 при расстоянии между ними в 1м и разности температур в 1 градус, т.е. при единичном градиенте температуры; [λ]= [Вт/м·К]. Уравнение (С) можно записать через
где Молекулярный перенос вещества можно выразить первым законом Фика
Физический смысл D: количество распределяемого компонента, которое переносится в 1с между двумя параллельными площадками в 1м2 при расстоянии между ними в 1м и при единичной разности концентрации. Как видно, приведенные законы молекулярного переноса описываются аналогичными уравнениями. Для газов эта аналогия очень близка, т.к. ν≈a≈D, для капельных жидкостей аналогия имеет ограниченный характер. Б) Дифференциальные уравнения переноса субстанции в движущейся жидкости (Навье-Стока, Фурье-Кирхгофа и Фика). Запишем уравнение переноса импульса для несжимаемой вязкой (идеальной) жидкости объемом
С одной стороны, уравнение (А) можно трактовать как баланс сил, действующих на элементарный движущийся объем жидкости. С другой стороны, уравнение (А) – это ОБС.
Запишем уравнение переноса теплоты в движущейся жидкости (
Запишем уравнение переноса вещества (массы) в движущейся жидкости (D=const, среда однофазная, изотропная, неразрывная):
с – концентрация вещества [с]= [кмоль/м3];
Лекция №5 Теория подобия В ХТП имеет место множество технологических параметров (). Получить математическую модель ХТП (систему уравнений и неравенств, адекватно описывающую данный процесс) можно аналитически. Но при этом получаются трудноразрешимые дифференциальные уравнения. Поэтому применяют моделирование ХТП – метод исследования процессов на моделях, отличающихся от натуры (промышленного аналога) в основном масштабом. Различают два метода моделирования: 1) метод теории подобия (обобщенных переменных), т.е. физическое моделирование; 2) метод численного эксперимента (математическое моделирование). Для конкретного процесса надо учитывать определенные ограничения. Поэтому математическую модель необходимо дополнить условиями однозначности. К ним относятся: 1) геометрическая форма (конструкция и размеры аппаратов); 2) физические свойства компонентов; 3) начальные условия (начальная температура, начальная концентрация и т.д.); 4) граничные условия (например, скорость жидкости на стенке равна нулю). Расчетные соотношения в обобщенных переменных (критериальные уравнения) получают опытным путем. Однако эксперименты проводят не на натурных объектах (промышленных аппаратах), а на их лабораторных моделях. Натура и модель должны отвечать определенным требованиям, которые устанавливает теория подобия. Теория подобия – учение о методах научного обобщения результатов экспериментов для подобных процессов и явлений. Для подобия натуры и модели между ними должно иметь место геометрическое, физическое, временное подобие, а также подобие начальных и граничных условий. Подобие можно задавать с помощью констант и инвариантов подобия. Пусть имеются промышленный цилиндрический аппарат и его лабораторная модель. H и h – высота, D и d – диаметр аппарата и модели, 0’, 0”, 1’, 1”, 2’, 2”, … - сходственные точки в рабочем объеме аппарата и лабораторной модели.
Запишем константу геометрического подобия (масштабный множитель):
Составим константу подобия скоростей:
Аналогично записываются константы плотностей, давлений, вязкостей и т.п. Константа временного подобия: При временном подобие натуры и модели интервалы времени, в течение которых частицы жидкости в них проходят геометрически подобные траектории, находятся в постоянных соотношениях. При подобии начальных и граничных условий постоянны отношения значений параметров в начале и на границах систем (натура и модели). Константы подобия зависят от соотношения размеров натуры и модели. Это создает трудности при масштабном переходе от модели к аппарату. Инвариатные подобия не зависят от соотношения размеров натуры и модели. Инварианты подобия составляют в виде отношений сходственных величин в пределах одной системы. Запишем инвариант геометрического подобия:
Составим инвариант вязкостей:
Инвариант подобия, составленный из однородных величин, - параметрический критерий (симплекс). Например, H/D – геометрический симплекс. Инвариант подобия, составленный из разноименных величин, - критерий подобия. Критерии подобия безразмерны. Подобные процессы и явления характеризуются численно равными критериями подобия.
Гидродинамическое подобие Критерии гидродинамического подобия можно получить двумя способами: 1) методом анализа размерностей физических величин; 2) масштабным преобразованием уравнений Навье-Стокса. Запишем уравнение Навье-Стокса для вертикальной оси z:
Сделаем подобные замены:
Взяв отношения приведенных комплексов к
l – характерный (определяющий) линейный размер (внутренний диаметр трубы, диаметр твердой частицы, эквивалентный диаметр зернистого слоя и т.п.). Равенство критериев Re, Fr, Eu и Ho, т.е. основных критериев гидродинамического подобия, в сходственных точках натуры и модели – необходимое и достаточное условие их гидродинамического подобия. В процессе естественной конвекции практически невозможно измерить скорость ω. Поэтому ее исключают:
Критериальные уравнения движения жидкости. Эти уравнения – решение уравнений Навье-Стокса. В общем виде:
Для стационарного потока уравнение (А) упрощается: Критериальные уравнения движения жидкости удобно представить в виде степенной зависимости:
где Г – геометрический симплекс (например, Величины А, m, n, p и q определяют опытным путем, например, с использованием метода наименьших квадратов. Критерий Eu – определяемый, остальные критерии – определяющие. При проведении гидравлических расчетов возникает необходимость определения Вначале находят все величины в правой части уравнения (С). Затем вычисляют критерий Eu. И, наконец, находят Перепад давлений Лекция №6 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
 , а для стационарных (непрерывных) процессов - единицу времени, например, 1сек.
, а для стационарных (непрерывных) процессов - единицу времени, например, 1сек.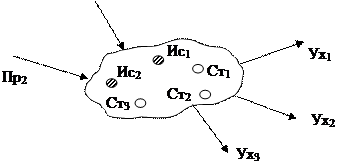
 .
. - градиент температуры; q – удельный тепловой поток [q]= [Дж/с ·м2].
- градиент температуры; q – удельный тепловой поток [q]= [Дж/с ·м2].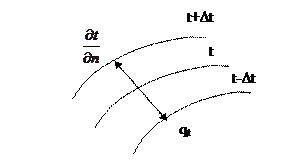
 (А)
(А) (В)
(В) (С)
(С) (энтальпию единицы объема жидкости):
(энтальпию единицы объема жидкости): (Д),
(Д), - коэффициент температуропроводности, м2/с.
- коэффициент температуропроводности, м2/с.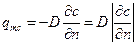 (Е), где D – коэффициент молекулярной диффузии; [D]= [м2/с].
(Е), где D – коэффициент молекулярной диффузии; [D]= [м2/с]. для оси z:
для оси z: - уравнение Навье-Стока для нестационарного потока, где
- уравнение Навье-Стока для нестационарного потока, где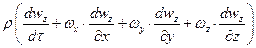 - сила инерции;
- сила инерции; - сила тяжести;
- сила тяжести; - сила давления;
- сила давления; - сила внутреннего трения;
- сила внутреннего трения; - проекции скорости на оси координат.
- проекции скорости на оси координат. - локальное накопление ( в данной точке) импульса во времени;
- локальное накопление ( в данной точке) импульса во времени;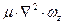 - накопление импульса за счет силы внутреннего трения;
- накопление импульса за счет силы внутреннего трения; - оператор Лапласа (лапласиан), т.е. сумма вторых производных по координатным осям.
- оператор Лапласа (лапласиан), т.е. сумма вторых производных по координатным осям. , среда – однофазная, неразрывная, изотропная):
, среда – однофазная, неразрывная, изотропная): - уравнение Фурье-Кирхгофа для нестационарного потока
- уравнение Фурье-Кирхгофа для нестационарного потока соответствует локальному накоплению теплоты во времени средой объемом
соответствует локальному накоплению теплоты во времени средой объемом  отвечает накоплению теплоты за счет конвекции;
отвечает накоплению теплоты за счет конвекции; выражает перенос теплоты кондукцией (теплопроводностью).
выражает перенос теплоты кондукцией (теплопроводностью). характеризует теплопоглощение (тепловыделение) внутри контура
характеризует теплопоглощение (тепловыделение) внутри контура  - источник (или сток) теплоты в единице объема и в единицу времени [Дж/м3·с].
- источник (или сток) теплоты в единице объема и в единицу времени [Дж/м3·с]. - уравнение Фика для нестационарного потока
- уравнение Фика для нестационарного потока соответствует локальному накоплению вещества во времени за счет изменения его концентрации в данной точке;
соответствует локальному накоплению вещества во времени за счет изменения его концентрации в данной точке; отвечает накоплению вещества за счет конвекции;
отвечает накоплению вещества за счет конвекции; характеризует молекулярный перенос компонента;
характеризует молекулярный перенос компонента; выражает возникновение (исчезновение) вещества в объеме
выражает возникновение (исчезновение) вещества в объеме  Если аппарат и модель подобны, то отношения их сходственных величин должны быть постоянны. Константу подобия составляют в виде отношения однородных (одноименных) сходственных величин.
Если аппарат и модель подобны, то отношения их сходственных величин должны быть постоянны. Константу подобия составляют в виде отношения однородных (одноименных) сходственных величин.
 .
.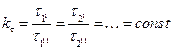
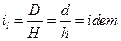 (одно и то же).
(одно и то же). .
. .
. – соответствует нестационарности потока;
– соответствует нестационарности потока;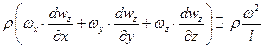 – характеризует силы инерции;
– характеризует силы инерции; – отвечает силам тяжести;
– отвечает силам тяжести; – выражает силы давления;
– выражает силы давления; – соответствует силам трения (вязкости).
– соответствует силам трения (вязкости).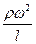 , получим критерий гидродинамического подобия:
, получим критерий гидродинамического подобия: – критерий Рейнольдса (мера соотношения сил инерции и вязкости (трения) в потоке жидкости.)
– критерий Рейнольдса (мера соотношения сил инерции и вязкости (трения) в потоке жидкости.) – критерий Фруда (мера соотношения сил инерции и гравитации в потоке жидкости).
– критерий Фруда (мера соотношения сил инерции и гравитации в потоке жидкости). – критерий Эйлера (мера соотношения изменения сил гидростатического давления к силам инерции в потоке жидкости).
– критерий Эйлера (мера соотношения изменения сил гидростатического давления к силам инерции в потоке жидкости). – критерий гомохронности (характеризует нестационарный характер потока жидкости).
– критерий гомохронности (характеризует нестационарный характер потока жидкости). – критерий Галилея (мера соотношения сил гравитации и вязкости в потоке жидкости).
– критерий Галилея (мера соотношения сил гравитации и вязкости в потоке жидкости).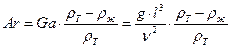 – критерий Архимеда (мера соотношения сил тяжести, трения и подъемной силы в потоке жидкости).
– критерий Архимеда (мера соотношения сил тяжести, трения и подъемной силы в потоке жидкости). (А) –для нестационарного потока.
(А) –для нестационарного потока. (В).
(В). , (С)
, (С) ).
). – гидравлического сопротивления трубопровода, аппарата и т.д.
– гидравлического сопротивления трубопровода, аппарата и т.д. .
.