
|
|
Тепловое подобие (подобие процессов теплоотдачи).Критерии теплового подобия можно получить с использованием уравнения конвективного переноса тепловой энергии – уравнения Фурье-Кирхгофа:
Произведем следующие замены: (А) (В) (С) Разделим (С) на (А):
Разделим (В) на (С):
Рассмотрим тепловые подобие с учетом граничных условий для турбулентного потока.
Конвекция усложняется за счет образования у стенки пограничного ламинарного гидродинамического слоя толщиной δг. В этом слое конвекция затухает. Это вызывает появление пограничного теплового слоя толщиной δт. Обычно δг и δг неодинаковы. В пограничном тепловом слое возникает значительный перепад температур и в нем тепло переносится преимущественно теплопроводностью. Таким образом, в ядре потока тепло переносится в основном конвекцией (скорость конвекции намного выше, чем кондукции), а в пограничном слое – теплопроводностью. Тепловой поток через пограничный слой по уравнению Фурье:
Тепловой поток из ядра потока к стенке (за счет теплоотдачи) можно найти по закону охлаждения Ньютона (уравнение теплоотдачи):
Для стационарного процесса:
Сделаем подобное преобразование уравнение (Д): (Е): Разделим (F) на (Е):
Тепловой критерий Прандтля получают комбинированием критериев Pe и Re:
Для теплоотдачи в условиях естественной конвекции применяют аналог критерия Архимеда
Для расчета теплоотдачи (стационарный процесс, вынужденная конвекция) используют критериальное уравнение:
Для естественной конвекции:
По этим критериальным уравнениям определяют коэффициенты теплоотдачи α, далее вычисляют коэффициент теплопередачи К и, наконец, поверхность теплопередачи F по основному уравнению теплопередачи:
Массообменное (диффузионное) подобие (подобие процессов массопередачи). Диффузионные критерии можно получить подобным преобразованием уравнения конвективной диффузии Фика:
(А) (В) (С) Разделим (С) и (А):
Fo′ – аналог Разделим (В) на (С):
Ре′ – аналог Аналогично тепловому критерию Нуссельта
Иногда его называют критерий Шервуда: Диффузионный критерий Прандтля:
Лекция № 7 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
 .
. - характеризует локальное накопление теплоты во времени;
- характеризует локальное накопление теплоты во времени; - соответствует конвективному теплопереносу;
- соответствует конвективному теплопереносу; - отвечает кондуктивному переносу теплоты (теплопроводностью).
- отвечает кондуктивному переносу теплоты (теплопроводностью). - критерий Фурье (мера соотношения локальных накоплений теплоты за счет кондукции и во времени). Критерий Фурье характеризует нестационарные условия теплопереноса и является аналогм критерия гомохронности Ho.
- критерий Фурье (мера соотношения локальных накоплений теплоты за счет кондукции и во времени). Критерий Фурье характеризует нестационарные условия теплопереноса и является аналогм критерия гомохронности Ho. - критерий Пекле (мера соотношения конвективного и кондуктивного теплоперноса).
- критерий Пекле (мера соотношения конвективного и кондуктивного теплоперноса).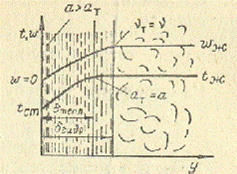
 .
. , где α – коэффициент теплоотдачи.
, где α – коэффициент теплоотдачи.
 . (Д)
. (Д)
 .
. – критерий Нуссельта (мера соотношения суммарного переноса теплоты конвекцией и теплопроводностью (т.е. теплоотдачей) и кондуктивного теплопереноса). Здесь l – определяющий геометрический размер (например, диаметр трубы).
– критерий Нуссельта (мера соотношения суммарного переноса теплоты конвекцией и теплопроводностью (т.е. теплоотдачей) и кондуктивного теплопереноса). Здесь l – определяющий геометрический размер (например, диаметр трубы). – критерий Прандтля (характеризует подобие скоростного и теплового полей). Для газов Pr≈1, для жидкостей Pr=10-100.
– критерий Прандтля (характеризует подобие скоростного и теплового полей). Для газов Pr≈1, для жидкостей Pr=10-100. – критерий Грасгофа (мера соотношения сил тяжести, вязкости и подъемной силы). β –коэффициент объемного расширения жидкости К-1; ∆t – разность температур поверхности стенки и жидкости.
– критерий Грасгофа (мера соотношения сил тяжести, вязкости и подъемной силы). β –коэффициент объемного расширения жидкости К-1; ∆t – разность температур поверхности стенки и жидкости. .
. .
. , где ∆tcр – средний температурный напор, Q – тепловой поток, Вт.
, где ∆tcр – средний температурный напор, Q – тепловой поток, Вт.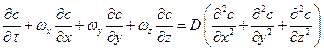 .
. – соответствует локальному накоплению вещества во времени;
– соответствует локальному накоплению вещества во времени; – отвечает конвективному массопереносу;
– отвечает конвективному массопереносу; – характеризует перенос вещества за счет молекулярной диффузии.
– характеризует перенос вещества за счет молекулярной диффузии. – диффузионный критерий Фурье (мера соотношения накоплений вещества за счет молекулярной диффузии и во времени).
– диффузионный критерий Фурье (мера соотношения накоплений вещества за счет молекулярной диффузии и во времени). .
.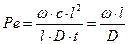 – диффузионный критерий критерий Пекле (мера соотношения переноса вещества конвективной диффузией и молекулярной диффузией).
– диффузионный критерий критерий Пекле (мера соотношения переноса вещества конвективной диффузией и молекулярной диффузией). .
. получают диффузионный критерий Нуссельта:
получают диффузионный критерий Нуссельта: – мера соотношения скоростей массоотдачи (совместный перенос вещества конвективной и молекулярной диффузией) и молекулярного переноса.
– мера соотношения скоростей массоотдачи (совместный перенос вещества конвективной и молекулярной диффузией) и молекулярного переноса. .
. – мера соотношения профилей скоростей и концентраций, т.е. толщин гидродинамического и диффузионного пограничных слоев. Иногда его называют критерием Шмидта:
– мера соотношения профилей скоростей и концентраций, т.е. толщин гидродинамического и диффузионного пограничных слоев. Иногда его называют критерием Шмидта:  .
.