
|
|
Гидродинамическая структура потока.1.Общие понятия о структуре потоков. 2.Модель идеального вытеснения (МИВ). 3.Модель идеального перемешивания (МИП). 4.Ячеечная модель. 5.Диффузионная модель.
1. В потоке жидкости в аппарате или химическом реакторе имеют место как поперечный, так продольный (вдоль оси аппарата) перенос субстанции. Структура потока, т.е. распределение локальных скоростей жидкости в рабочей зоне аппарата зависит от многих факторов: от скоростей потоков, свойств компонентов, конструкции аппаратов и т.п. Для увеличения пропускной способности аппаратов и реакторов необходимо интенсифицировать поперечный перенос. Однако, при этом расчет скорость и продольного переноса, что в большинстве случаев снижает эффективность процесса. Цель ХТП – изменение какого-то свойства (температуры, концентрации и т.д.) рабочей среды во времени. Вследствие различия локальных скоростей время пребывания частиц жидкости в рабочей зоне аппарата или реактора также различно. Результирующая степень изменения целевого свойства среды зависит не только от среднего времени пребывания частиц жидкости в рабочей зоне, но и от функции распределения элементов потока по времени их пребывания в аппарате. Для измерения случайной величины – времени пребывания частиц жидкости в аппарате используют трассер (метку, индикатор). Это может быть раствор неорганической соли, краска и т.д. Метку в небольшом количестве вводят в поток на входе в рабочую зону аппарата, а затем измеряют концентрацию трассера на выходе из аппарата. Таким образом, получают зависимость. Таким образом, получают зависимость концентрации метки С от времени τ, т.е. выходную кривую, и кривую отклика. По этой кривой можно установить, какая часть жидкости от вошедшей в аппарат выйдет из него через данный интервал времени. Различают две идеальные модели структуры потока: 1) модель идеального вытеснения (поршневой, или стержневой поток); 2) модель идеального перемешивания.
2.
Рис. Эпюра локальных скоростей для МИВ. В режиме ИВ время пребывания в РЗ всех элементов потока, движущихся с одинаковой скоростью ω, одинаково:
Кривая отклика при импульсном (почти мгновенно) ввода дроссера для режима ИВ:
Пусть Тогда функция отклика описывается соотношением:
Таким образом, выходной сигнал фиксируется только в момент времени Часто выходной сигнал описывают безразмерными симплексами В этом случае кривая отклика характеризуется соотношениями:
МИВ – беспараметрическая модель. К МИВ можно отнести движение жидкости через пучок параллельных труб небольшого диаметра, через неподвижный зернистый слой. 3. В режиме идеального смешения частицы жидкости движутся с бесконечно большими скоростями во всех направлениях. В результате параметры потока (концентрации, температуры и т.д.) выравниваются во всех точках РЗ. Поэтому некоторые частицы жидкости могут попасть в выходной поток практически мгновенно, не успев пройти обработку. Иные частицы жидкости могут пребывать в РЗ бесполезно долго. Значит, здесь важно определить не только среднее время пребывания частиц жидкости
Если в момент времени τ=0 во входной поток ввести трассер, то он мгновенно равномерно распределится в РЗ. Его концентрация составит
а) в размерных величинах б) в безразмерных величинах. Как видно из графиков, трассер постепенно вымывается из РЗ. Функция распределения Для аппарата промежуточного типа (между МИВ и МИП) выходная кривая:
Время пребывания частиц жидкости в РЗ в случае МИП – величина случайная. Среднее время пребывания равно математическому ожиданию: Дисперсия σ2 характеризует среднее значение квадрата разброса времени пребывания относительно мат. ожидания: Продольное (обратное) перемешивание пропорционально дисперсии времени пребывания элементов потока в РЗ. К МИП близки аппараты с интенсивным перемешиванием (барботажные, с псевдоожиженным слоем и т.д.).
3.В ячеечной модели реальный аппарат делят на n одинаковых последовательно соединенных ячеек идеального перемешивания. Объем реального аппарата равен сумме объемов всех ячеек.
Ячеечная модель называется еще каскадная или ступенчатая. Объем одной ячейки
Кривые отклика для ячеечной модели:
При n = ∞ ячеечная модель превращается в МИВ, при n = 1 – в МИП. Дисперсия для ячеечной модели:
5. В основе модели – МИВ, осложненная обратным перемешиванием:
где DL – коэффициент продольной диффузии, учитывающий и молекулярную и турбулентную диффузию, а также неравномерность поля скоостей. За параметр диффузионной модели принимают критерий Пекле: При PeL = 0 (т.е. DL = ∞) диффузионная модель переходит в МИП. При ReL = ∞ ДМ→МИВ. В реальном аппарате: 0 < PeL < ∞.
Кривые отклика:
Дисперсию времени пребывания определяют по формуле: При PeL > 10 отклонение реального аппарата от МИВ небольшое:
Соотношение Лекция № 8 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|

 , где Q – объемный расход жидкости, V – объем рабочей зоны (РЗ), L – длина рабочей зоны.
, где Q – объемный расход жидкости, V – объем рабочей зоны (РЗ), L – длина рабочей зоны.
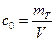 – начальная концентрация трассера в аппарате, где mT – количество введенного в поток трассера.
– начальная концентрация трассера в аппарате, где mT – количество введенного в поток трассера.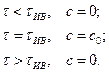
 (до этого момента трассер не дошел до выхода, а после этого момента он покинул РЗ).
(до этого момента трассер не дошел до выхода, а после этого момента он покинул РЗ).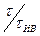 и
и 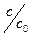 , т.е. приведенным временем и приведенной концентрацией трассера.
, т.е. приведенным временем и приведенной концентрацией трассера.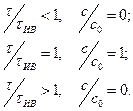
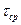 , но и распределение их по времени пребывания в РЗ
, но и распределение их по времени пребывания в РЗ  .
.  , где V – объем РЗ,Q – объемный расход жидкости.
, где V – объем РЗ,Q – объемный расход жидкости.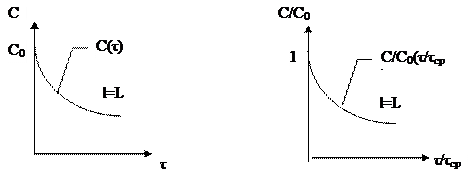
 для МИП имеет экспоненциальный характер:
для МИП имеет экспоненциальный характер:  .
. , т.к. трассер попадает в выходной поток не сразу.
, т.к. трассер попадает в выходной поток не сразу.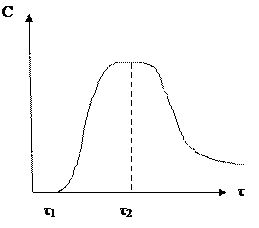
 – в размерном виде.
– в размерном виде.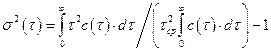 .
.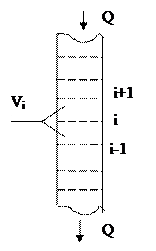
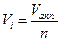 . Данную модель характеризует параметр n, т.е. число ячеек. Ячеечная модель описывается системой n линейных уравнений первого порядка:
. Данную модель характеризует параметр n, т.е. число ячеек. Ячеечная модель описывается системой n линейных уравнений первого порядка: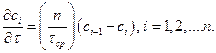
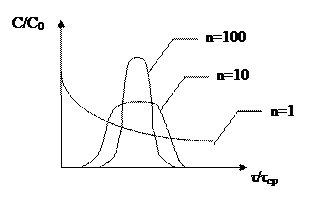
 .
. ,
, , где ω – скорость потока, L – длина аппарата.
, где ω – скорость потока, L – длина аппарата.
 .
. .
.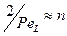 описывает соотношение между ячеечной и диффузионной моделями. К ДМ близки насадочные, пленочные, распылительные аппараты с ограниченным отношением
описывает соотношение между ячеечной и диффузионной моделями. К ДМ близки насадочные, пленочные, распылительные аппараты с ограниченным отношением  .
.