
|
|
Занятие 3. Дифракция света.Краткие теоретические сведения Основные формулы Под дифракцией света понимают явление огибания светом встречных препятствий (отклонение от законов геометрической оптики), которое обусловлено его волновой природой. Радиусы зон Френеля в случае плоского волнового фронта:
где При дифракции параллельного пучка лучей монохроматического света на одной узкой щели направления, в которых наблюдаются максимумы света, определяются из условия:
где Направления, в которых наблюдаются минимумы света, определяются из условия:
При дифракции на плоской решетке направления, в которых наблюдаются максимумы света, определяются из условия:
где Разрешающая сила дифракционной решетки:
где Разрешающая сила
где Угловая дисперсия решетки:
Для малых углов справедливо приближенное равенство:
При дифракции рентгеновских лучей на кристаллической решетке направления, в которых имеет место дифракционный максимум, определяются по уравнению Вульфа-Брегга:
где Вопросы для ответа у доски 1. Зоны Френеля. Выполните рисунок. Рассчитайте радиусы зон Френеля. 2. Дифракция Френеля на круглом отверстии. Выполните рисунок. Рассчитайте число зон Френеля, укладывающихся в отверстии. 3. Дифракция Франгофера на щели. Дифракционная решетка. Выполните рисунок. Определите ширину дифракционной полосы. Запишите условия дифракционного максимума и минимума. Примеры решения задач Задача 1. На щель шириной 0,1 мм нормально падает параллельный пучок света от монохроматического источника ( Решение. Центральный максимум интенсивности света занимает область между ближайшими от него справа и слева минимумами интенсивности. Поэтому ширину центрального максимума интенсивности примем равной расстоянию между этими двумя минимумами интенсивности (Рис. 1).
Минимумы интенсивности света при дифракции от одной щели наблюдаются под углами
где Расстояние между 2–мя минимумами на экране определим непосредственно по чертежу:
При малых углах Выразим
Произведя вычисления по формуле (3), получим:
Ответ: Задача 2. Найти наибольший порядок спектра для жёлтой линии натрия с длиной волны Решение. Воспользуемся формулой дифракционной решетки d×sinj =kl, откуда: k=d×sinj/l. Из этого выражения видно, что при заданных d и l порядок спектра k будет максимальным, когда sinj =1, т.е. при угле отклонения 1,57 рад. Следовательно, kmax = Ответ: kmax»3. Задача 3. Определить угол дифракции для второго порядка света натрия с длиной волны l=589 мкм, если на 1 мм дифракционной решетки приходится пять штрихов. Решение. Из формулы дифракционной решетки d×sinj =kl, найдём: sinj =kl/d, Поскольку число штрихов, отнесённых к длине решётки, связано с периодом решетки соотношением N0 = 1/d, то можно записать sinj = klN0, откуда j =arcsin klN0; тогда получаем: j =arcsin (2×5,89×10-7×5×103 ) рад=5,8×10-3 рад. Ответ: 5,8 10-3 рад. Задача 4. Плоская световая волна (длина волны Решение. Зоны Френеля в данном случае удобно выбрать в виде полосок, параллельных краям щели. В направлении
четыре зоны Френеля.
Отсюда: Следовательно, в направлении Ответ: минимум будет наблюдаться, если Задача 5. Определить оптимальные размеры отверстия “дырочной” камеры в зависимости от длины волны, т.е. радиус отверстия r, при котором точечный источник изобразится на стенке камеры кружком минимального диаметра, если расстояние от источника света до камеры велико по сравнению с ее глубиной d. Направления на минимумы освещенности по порядку величины определяются той же формулой, что и для щели, только вместо ширины щели нужно взять диаметр отверстия 2r. Решение. Лучи, падающие на отверстие камеры от удаленного точечного источника, идут приблизительно параллельно. Если бы не было дифракции, то размеры светлого пятна были бы равны AB=2r (Рис. 3). Вследствие дифракции размеры пятна увеличатся до DC.
Расстояние ОС определяется углом
Эта величина достигает максимума при Оптимальные размеры отверстия: Ответ: Домашнее задание: [Л-3] - 16.28, 16.29, 16.30, 16.32, 16.34, 16.35, 16.36,16,37,16.38; [Л-4] - 4.39, 4.40, 4,41, 4.46, 4.53; [Л-5] - 5.71, 5.78, 5.82, 5.85, 5.91, 5.101. Вопросы для самопроверки 1. В чем состоит явление дифракции света? 2. В чем заключается принцип Гюйгенса? Какое дополнение ввел Френель в принцип Гюйгенса? 3. Суть метода графического сложения амплитуд? 4. Что представляет собой зонная пластинка? 5. Что можно наблюдать на экране при дифракции на одной щели в параллельных лучах, если ширина щели равна длине волны света? 6. Дифракционная решетка и ее основные характеристики? 7. Условия главных максимумов и главных минимумов дифракционной решетки? 8. Разрешающая способность дифракционной решетки (условие Рэлея)? 9. Почему в природе дифракция звуковых волн более очевидна, чем дифракция световых волн? 10. В чем отличие дифракции Фраунгофера от дифракции Френеля? 11. Можно ли наблюдать дифракционные картины на отверстиях радиусом порядка нескольких сантиметров? 12. Как происходит перераспределение потока световых волн на дифракционной решетке? 13. Каким способом можно определить длину световой волны с помощью дифракционной решетки? 14. Как изменится дифракционная картина, если закрыть половину решетки? 15. Как изменяется дифракционная картина от двух щелей по сравнению с дифракционной картиной от одной щели? 16. Источник белого света, дифракционная решетка и экран помещены в воду. Какие изменения претерпит при этом дифракционная картина, если углы отклонения световых лучей решеткой малы? 17. Найти условие, определяющее направление на главные максимумы при наклонном падении световых волн на решетку, если период решетки Задачи для самостоятельного решения 1. Свет от монохроматического источника (длина волны 0,6 мкм) падает нормально на диафрагму с круглым отверстием. Диаметр отверстия 6 мм. За диафрагмой на расстоянии 5 м от нее находится экран. 1) Сколько зон Френеля укладывается в отверстии диафрагмы? 2) Каким будет центр дифракционной картины на экране: темным или светлым? 2. Вычислить радиусы первых пяти зон Френеля, если расстояние от источника света до волновой поверхности 1 м, расстояние от волновой поверхности до точки наблюдения также 1 м и длина волны 3. Вычислить радиусы первых пяти зон Френеля для случая плоской волны. Расстояние от волновой поверхности до точки наблюдения 1 м. Длина волны 4. На дифракционную решетку с периодом 2,5·103 мм падает монохроматический свет длиной волны 5. Сколько штрихов на каждый сантиметр содержит дифракционная решетка, если при наблюдении в монохроматическом свете (длина волны 0,25 мкм) максимум четвертого порядка отклонен на угол 120 . 6. Монохроматический свет падает нормально на дифракционную решетку, имеющую 250 штрихов на 1 мм. Второй дифракционный максимум, наблюдаемый на экране, смещен от центрального на угол 200. определить длину волны 7. На дифракционную решетку падает нормально монохроматический свет ( 8. На дифракционную решетку, содержащую 50 штрихов на 1 мм, падает нормально монохроматический свет. Зрительная труба спектрометра наведена на спектр третьего порядка, чтобы видеть другой спектр третьего порядка трубу повернули на угол 100. Определить длину световой волны. 9. При освещении дифракционной решетки монохроматическим светом 10. Определить число штрихов на 1 мм дифракционной решетки, если при нормальном падении монохроматического света 11. Дифракционная решетка, освещенная нормально падающим монохроматическим светом, отклоняет максимум второго порядка на расстояние 5,8 см от центрального. Постоянная решетки равна 0,01 мм экран находится на расстоянии 0,5 м от дифракционной решетки. Определить длину волны падающего света. 12. На дифракционную решетку, содержащую 50 штрихов на 1 мм, падает нормально монохроматический свет 13. Параллельный пучок белого света падает нормально на дифракционную решетку с периодом 0,02 мм длина волны крайних красных и фиолетовых лучей 14. На щель шириной 2мкм подается нормально параллельный пучок монохроматического света с длиной волны 15. На щель шириной 2·10-3 см падает нормально параллельный пучок монохроматического света с длиной волны 5·10-5 см. найти ширину изображения щели на экране, удаленной от щели на 1 м. Шириной изображения считать расстояние между первыми дифракционными минимумами, расположенными по обе стороны от главного максимума освещенности. 16. Сколько штрихов на 1мм длины имеет дифракционная решетка, если зеленая линия ртути 17. На дифракционную решетку нормально падает пучок света от разрядной трубки. Чему должна быть равна постоянная дифракционной решетки, чтобы в направлении угла дифракции 410 совпадали максимумы двух линий: 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|

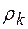 - радиус зоны;
- радиус зоны;  - номер зоны;
- номер зоны;  - расстояние от круглого отверстия в непрозрачном экране до точки наблюдения, расположенной на оси отверстия;
- расстояние от круглого отверстия в непрозрачном экране до точки наблюдения, расположенной на оси отверстия;  - длина световой волны.
- длина световой волны.
 - ширина щели;
- ширина щели; 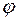 - угол отклонения лучей от нормали к плоскости щели;
- угол отклонения лучей от нормали к плоскости щели; 

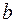 - ширина непрозрачного штриха;
- ширина непрозрачного штриха;  -период решетки (постоянная решетки);
-период решетки (постоянная решетки); 
 - наименьшая разность длин волн двух соседних спектральных линий (
- наименьшая разность длин волн двух соседних спектральных линий (  ), при которой эти линии могут быть видны раздельно в спектре, получаемом посредством данной решетки.
), при которой эти линии могут быть видны раздельно в спектре, получаемом посредством данной решетки. решетки тем больше, чем больше штрихов содержит решетка, и чем больше порядковый номер
решетки тем больше, чем больше штрихов содержит решетка, и чем больше порядковый номер 
 - полное число штрихов решетки.
- полное число штрихов решетки.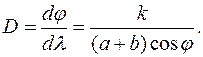
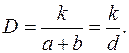
 ,
, - расстояние между атомными плоскостями;
- расстояние между атомными плоскостями; 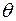 - угол между направлением рентгеновских лучей, падающих на кристалл, и гранью кристалла.
- угол между направлением рентгеновских лучей, падающих на кристалл, и гранью кристалла. ). Определить ширину
). Определить ширину  центрального максимума в дифракционной картине, проецируемой с помощью линзы, находящейся непосредственно за щелью, на экран, отстоящий от линзы на расстоянии
центрального максимума в дифракционной картине, проецируемой с помощью линзы, находящейся непосредственно за щелью, на экран, отстоящий от линзы на расстоянии 

 ,
,

 тогда:
тогда:  (2).
(2). из формулы (1) и подставим его в равенство (2):
из формулы (1) и подставим его в равенство (2):
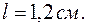

 м, если период дифракционной решетки 2 мкм.
м, если период дифракционной решетки 2 мкм. .
. ) падает нормально на узкую щель ширины b. Определить направления на минимумы.
) падает нормально на узкую щель ширины b. Определить направления на минимумы. будет наблюдаться минимум в том случае, если в щели АВ (Рис. 2) укладывается четное число волн. На Рис. 2 изображено
будет наблюдаться минимум в том случае, если в щели АВ (Рис. 2) укладывается четное число волн. На Рис. 2 изображено
 где
где  - ширина зоны Френеля, k=1, 2, 3, … АК представляет собой разность хода между крайними лучами, посылаемые одной зоной:
- ширина зоны Френеля, k=1, 2, 3, … АК представляет собой разность хода между крайними лучами, посылаемые одной зоной:

 .
.
 . Следовательно, радиус пятна:
. Следовательно, радиус пятна:

 .
. , где
, где  5,7·10-7 м.
5,7·10-7 м. . На каком расстоянии от дифракционной решетки находится экран, если второй дифракционный максимум смещен на 20 см от центрального.
. На каком расстоянии от дифракционной решетки находится экран, если второй дифракционный максимум смещен на 20 см от центрального. и
и  . Вычислить ширину спектра первого порядка, если экран находится на расстоянии 1,8 м от решетки.
. Вычислить ширину спектра первого порядка, если экран находится на расстоянии 1,8 м от решетки. . Найти углы, в направлении которых будут наблюдаться минимумы света.
. Найти углы, в направлении которых будут наблюдаться минимумы света. в спектре первого порядка наблюдается под углом 1908¢?
в спектре первого порядка наблюдается под углом 1908¢? =
=  и
и 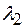 =
=  ?
?