
|
|
Сопротивление движению потокаГидродинамический напор для жидкости, вытекающей из трубы, выражается зависимостью Н = где hп – потеря напора, обусловленная преодолением сопротивления течению (сопротивление трения о стенки, либо возникающее при изменении направления движения жидкости). Можно показать, что Н = z - коэффициент сопротивления трения. hп = z z - является функцией Re. z = f (Re) l/d, где l и d – соответственно длина и диаметр трубопровода. Приняв hп равным Dр/r, где Dр – потеря давления, кг/м2, имеем: Dр = f(Re) f(Re) – коэффициент трения. Пусть f(Re) = l, тогда Dр = l или Dр = z Для ламинарного течения жидкости l = z = В условиях турбулентного движения используются эмпирические уравнения (3 × 103 £ Re £ 105). l = При Re > 5000 можно использовать и зависимость l =
НЕКОТОРЫЕ ЗАКОНОМЕРНОСТИ ФИЛЬТРАЦИИ
Процесс фильтрации широко используется в процессах обезвреживания, переработки и утилизации отходов. Выделение твердой фазы с высоким содержанием токсичных компонентов необходимо: - для их выделения из нее и последующего разделения; - для утилизации входящих в осадок продуктов; - для переработки ценных составляющих. Фильтрация используется при разделении суспензий, если недопустима потеря жидкости (дисперсной фазы), особенно, если частицы последней плохо оседают, либо необходимо получить ее с минимальным содержанием дисперсионной среды, т. е. с низкой влажностью. Этот процесс позволяет разделять суспензии в очень широком интервале размеров частиц твердой фазы. Следует иметь в виду, что для проведения фильтрации необходимо преодолеть гидравлическое сопротивление, обусловленное как фильтром (фильтрующей перегородкой), так и образующимся осадком. Причем эффект влияния перегородки значим лишь в начальный период фильтрации. Его вклад снижается во времени по мере роста толщины осадка, гидравлическое сопротивление которого быстро становится определяющим. В связи с этим первые порции фильтрата, как правило, недостаточно очищены от диспер- Природа, толщина и структура осадка, отлагающегося на фильтре – в большинстве случаев факторы, определяющие эффективность фильтрации, в том числе производительность фильтрующего оборудования и расход электроэнергии. Скорость фильтрации Сф – один из важнейших показателей этого процесса. Она характеризуется количеством фильтрата, проходящего через единицу поверхности фильтрующей перегородки за единицу времени. Сф = Размерность Сф - м3/м2×с (м×с-1), где Vф и S – соответственно объем фильтрата и сечение фильтра. Сф является функцией давления суспензии, толщины и природы осадка. Из самых общих соображений можно выделить два типа осадков: - представленные практически недеформируемыми частицами; - сжимаемые осадки, состояние из деформируемых частиц (обычно аморфных). В первом случае взаимное расположение и размеры пор не зависят от изменения давления. Например, его рост с 0,7 до 4,0 кг/см2 не изменяет объема фильтрата. Промывка осадка Промывание осадка ведет к удалению из осадка загрязняющих веществ, в том числе и экотоксикантов, особенно, если они растворяются в промывной жидкости существенно лучше, чем основное вещество. Одновременно этот процесс обусловливает увеличение объема фильтрата и расхода энергии на упаривание. В связи с этим необходимо использовать минимальный объем промывной жидкости. Выясним, что целесообразнее: многократное промывание осадка малым объемом или однократное, но значительным ее количеством (Vф = const). Рассмотрим этот вопрос более подробно. Пусть V0 – объем промывной жидкости, остающийся в осадке и не стекающий через фильтр, V1 – объем очередной порции промывной жидкости, С0 – начальная концентрация отмываемого вещества. После первой порции имеем: С1 = С0V0/(V0 + Vi), где С1 – концентрация отмываемого вещества. С2 = С1V0/(V0 + Vi), С1 = С0V Пусть общий объем промывной жидкости – 100 условных единиц, т. е. в 100 раз больше V0. Каждая порция – 50 или 25 условных единиц. Тогда имеем: С4 = С0/(1 + 25)4; С4 = 2,19 × 10-6 С0 С2 = С0/(1 + 50)2; С2 = 3,84 × 10-4 С0, т. е. С4 << С2. Таким образом, выгоднее промывать малыми объемами многократно. Часто промывание осадка производят насыщенным раствором основного вещества, предотвращая переход его в фильтрат. Отметим, что согласно экспериментальным данным, протекание фильтруемой жидкости через поры фильтрующей перегородки и осадка носит ламинарный характер. Движение ее в капиллярах подчиняется уравнению V = где V – объем жидкости, r и l – радиус капилляра и его длина, m - динамическая вязкость, Dр и t - соответственно перепад давления на входе и выходе фильтра и продолжительность фильтрации. Предполагается, что капилляры имеют правильную цилиндрическую форму. Пусть n – число капилляров на единице площади фильтрующей поверхности, a ³ 4 – коэффициент, учитывающий их извилистость. Тогда l = ah, h – толщина слоя осадка и уравнение (52) принимает вид V = Удельная скорость фильтрации (отнесенная к единице поверхности) равна Сф = и Сф = Реально, в силу протекания побочных факторов, зависимость Сф от Dр не является линейной. Оценим отдельно вид (53б) для фильтра
и слоя осадка
Пусть 8aI / pnir Тогда (54а) и (55а) принимают вид
и
В силу непрерывности потока через фильтрующую перегородку и слой осадка после несложных преобразований имеем:
Dр1 + Dр2 = Dр0. Откуда
Так как Dр2 >> Dр1, получаем (опустив нижние индексы)
c - имеет смысл удельного сопротивления осадка с размерностью м-2. Следует учитывать связь между промежуточным процессом фильтрации с образованием осадка и им же по стандартному закону при постепенном сужении капилляров в силу прилипания частиц дисперсной фазы к их стенкам. При Dр = const (t - продолжительность фильтрации) t = ( где k1 – константа, м-1, характеризующая сопротивление потоку фильтруемой системы, vф,0 – начальная мгновенная скорость фильтрации, м/с. Величины k1 и vф,0 можно определить из зависимости: k1t = или для стандартного закона, учитывающего сжатие капилляров (Dр = const)
Если 1 м3 фильтрата создает на фильтре х, м2 осадка, то действительно равенство vx = hS0 и h = Сочетая уравнения (57) и (56), получим
или VdV = Dр0S Интегрируя (58) в пределах от 0 до V и от 0 до t, имеем V2 = 2Dр0S или М = где М = V/S0 – удельная производительность фильтра. Для фильтров непрерывного действия V, м3ч-1 = Для установок периодического действия V, м3ч-1 =
Контрольные вопросы 1. Запишите уравнения адсорбции Гиббса и Ленгмюра. 2. Какие существуют виды адсорбции? Чем они определяются? 3. Как определить значение констант в уравнении Ленгмюра? 4. Что такое абсорбция? Запишите уравнение Генри. 5. Как выражается критерий Рейнольдса? 6. Как целесообразно проводить промывку осадка при проведении фильтрации? Докажите. 7. Как можно рассчитать по объему фильтрата производительность фильтров непрерывного и периодического действия? 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
 + hп,
+ hп,
 , кг/м2,
, кг/м2, ,
, .
. (уравнение Филоненко).
(уравнение Филоненко). .
. /(V0 + Vi)2, Сn = С0V
/(V0 + Vi)2, Сn = С0V  /(V0 + Vi)n.
/(V0 + Vi)n. , (52)
, (52) .
.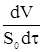 ; (53а)
; (53а) . (53б)
. (53б)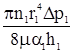 (54а)
(54а) . (55а)
. (55а) = ci.
= ci. (54б)
(54б) . (55б)
. (55б)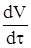 (mc1h1 + mc2h2) = S0(Dр1 + Dр2)
(mc1h1 + mc2h2) = S0(Dр1 + Dр2) .
. , м3/м2с (56)
, м3/м2с (56)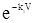 - 1)/k1vф,0,
- 1)/k1vф,0, -
- 
 =
=  .
. . (57)
. (57)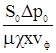
 ,
, .
. ; St = t + tпр + tр, где tпр и tр – длительности промыва и разгрузки, St - полная продолжительность одного цикла фильтрации.
; St = t + tпр + tр, где tпр и tр – длительности промыва и разгрузки, St - полная продолжительность одного цикла фильтрации.