
|
|
Выражение для движущей силы оседания имеет видFдвиж = 4/3pr3g(r - r0), r – радиус оседающей частицы. Движущей противодействует сила трения, величина которой определяется законом Стокса: Fтр = 6phrv, где h - динамическая вязкость дисперсионной среды, r – радиус частицы, v - скорость оседания. Через некоторый промежуток времени от начала седиментации движение частицы начнет протекать с постоянной скоростью (равномерное движение). В этом случае SF = 0, т. е. Fдвиж = Fтрения. Тогда 6phrv = 4/3pr3g(r - r0). (36) После несложных преобразований получаем зависимость для расчета скорости осаждения монодисперсных (r = const) частиц v = В случае газовой дисперсионной среды r >> r0, следовательно r0 можно пренебречь и уравнение (37) несколько упрощается v = Если r < r0, то v принимает отрицательные значения. Иначе говоря, вместо осаждения наблюдается всплытие частиц. Из уравнений (37) и (37а) следует, что скорость оседания (при r > r0) пропорциональна квадрату радиуса и плотности вещества дисперсной фазы и обратно пропорциональна динамической вязкости дисперсионной среды. Из зависимости (37) легко получить радиус седиментирующих частиц, если известна их скорость оседания r = или для случая аэрозолей (пренебрегая r0 для систем с газовой дисперсионной средой). r = Естественно, что после завершения оседания достаточно крупнодисперсных частиц в системе (в газовой или жидкой дисперсионной среде) остаются неспособные седиментировать наиболее мелкие частицы. Оседанию препятствует их участие в броуновском движении, что приводит к устойчивому квазиравновесному распределению таких частиц по высоте (h). Равновесное распределение подобных образований по h принято называть седиментационной или кинетической устойчивостью. Такое состояние характерно, прежде всего, для высокодисперсных систем (газы, истинные растворы). Коллоидные системы (аэро- и лиозоли) занимают промежуточное положение. Седиментации противодействует диффузионный поток вещества, интенсивность которого описывается зависимостью, называемой первым законом Фика, имеющим следующий вид ig = - D Если сечение диффузии S и время диффузии t принимают единичные значения, уравнение (38а) приобретает вид ig = - D где D – коэфициент диффузии и dС/dx – градиент концентрации (скорость изменения концентрации по направлению диффузионного потока). Величину потока седиментации (ic) можно выразить через его скорость и концентрацию дисперсной фазы ic = vC. Приняв 6phr = В, для силы трения имеем Fтр = Вv. Тогда при Fдвиж = Fтр. и v = const, mg = Вv, откуда v = ic = mgС/B, где m – эффективная масса частицы, В – эффективный коэффициент трения (6phr) между дисперсной фазой и дисперсионной средой, с – концентрация дисперсной фазы, g – ускорение свободного падения. Уравнение Фика можно записать иначе m = - D Величина D, в свою очередь, определяется зависимостью (уравнение Эйнштейна) D = R – универсальная газовая постоянная, N – число Авогадро, k – константа Больцмана. Разделив уравнение (39) на (38б), имеем: ic/ig = и, учтя (40), получаем ic/ig = - или ic/ig = - где V – объем частицы, k – константа Больцмана. При ic/ig >> 1 потоком диффузии можно пренебречь. Напротив, для случая ic/ig << 1 исчезающе мал поток седиментации. И лишь при соотношении ic/ig » 1 устанавливается определенное распределение частиц по высоте. В условиях интенсивного перемешивания dС/dx = 0. При прекращении перемешивания такой системы равномерное распределение нарушается, а производная dС/dx возрастает во времени. Этот эффект продолжается до тех пор, пока не выравнены потоки ig и ic, т. е. ic/ig = 1. Заменив х на h (распределение по высоте), имеем:
ln Для 1 моля частиц ln или С0/Сh = еmgh/kT. (42б) Так как давление пропорционально концентрации, то ln (42в) – гипсометрический закон Лапласа. Следует учесть, что концентрация дисперсной фазы пропорциональна частичной концентрации. Тогда уравнение (42а) для рассматриваемого случая можно представить в виде ln или h = Здесь n0 и nh – концентрация монодисперсных частиц соответственно в нулевой точке, взятой за исходную для отсчета и на расстоянии h от нее. Уравнение (43) позволяет оценить величину h, на которой соотношение Рассмотренный подход количественно справедлив только для монодисперсных систем, которые на практике практически не встречаются. Для инженерных расчетов, проводимых в случае полидисперсных систем, целесообразно оценивать связь между размером частиц и количеством седиментировавшего (перешедшего в осадок) вещества. Эту связь можно оценить из следующих соображений. Масса дисперсной фазы Мос прямо пропорциональна количеству вещества А в столбе рассматриваемой системы, скорости v и времени оседания t и обратно пропорциональна высоте столба h. Отсюда можно записать Мос = k k – коэффициент пропорциональности, равный 1. Сочетая уравнения (44) и (37), и, учтя плотность дисперсионной среды, получим Мос = Откуда r = Однако и уравнение (45) пригодно только для случая монодисперсных систем. Седиментация полидисперсной системы характеризуется кривой седиментации (рис. 5). На ней обычно хорошо выражен прямолинейный участок ОВ, отвечающий малым значением t. Абсцисса точки В соответствует времени полного выделения самой крупной фракции (t1) º (tмин). Цифра в нижнем индексе ti характеризует время оседания i–той фракции.
Рис. 5. Кривая седиментация полидисперсной системы. После установления предельных размеров самых крупных и мелких частиц, полидисперсную систему условно разбивают на фракции с радиусом частиц в заданных узких пределах. В общем случае берут фракции по кривой седиментации, выделив для этой цели серию точек в местах наибольшего изменения кривизны кривой ОG (рис. 5) – С, D, E и F. По абсциссам выбранных точек вычисляют максимальный и минимальный радиус частиц каждой фракции. При этом масса каждой фракции определяется по отрезкам, отсекаемым на оси ординат. Так отрезок
Контрольные вопросы 1. От чего зависит сила трения в соответствии с законом Стокса? 2. Получите выражение для скорости седиментации в гравитационном поле. Каков физический смысл отрицательной величины скорости седиментации? 3. Запишите выражение для 1-го закона Фика. 4. Что характеризует гипсометрический закон Лапласа? 5. Как можно определить фракционный состав седиментируемой полидисперсной системы?

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
 . (37)
. (37) . (37а)
. (37а)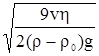
 .
. . (38а)
. (38а) , (38б)
, (38б) (39)
(39) . (40)
. (40)
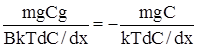
 , (41)
, (41) = 1
= 1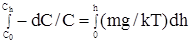
 = mgh/kT.
= mgh/kT. ; (42а)
; (42а) =
= 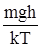 , (42в)
, (42в) =
=  . (43)
. (43)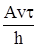 , (44)
, (44) .
.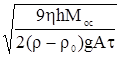 . (45)
. (45)
 соответствует Мос первой фракции,
соответствует Мос первой фракции, 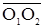 - второй,
- второй,  - третьей и т. д. Примем общую массу осадка, соответствующей длине отрезка
- третьей и т. д. Примем общую массу осадка, соответствующей длине отрезка  . Тогда можно определить относительное содержание каждой фракции. Так отношение
. Тогда можно определить относительное содержание каждой фракции. Так отношение