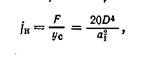|
|
Баланс жесткости шпиндельных узлов. Расчет шпиндельных узлов на жесткость.РАСЧЕТ ШПИНДЕЛЬНЫХ УЗЛОВ
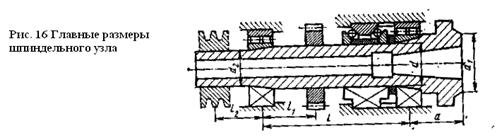
Расчет на жесткость. Главные размеры шпиндельного узла (рис. 16) — диаметр d шейки шпинделя под передней опорой и расстояние l между опорами — выбирают из расчета шпинделя на жесткость. Величину вылета а шпинделя определяют по стандартным размерам его переднего конца и размерам уплотнений; она должна быть возможно малой. При приближенных проектных расчетах шпиндель заменяют балкой на двух опорах с силой F, приложенной на консоли, т. е. на расстоянии а от середины передней опоры Радиальное перемещение переднего конца шпинделя У∑ = УШП + У ОП + УСДВ (1.4)
Где у шп— перемещение, вызванное изгибом тела шпинделя; уоп —перемещение, вызванное податливостью (нежесткостью) опор; усдв — перемещение, вызванное сдвигом от действия поперечных сил. Применяя известные формулы сопротивления материалов и пренебрегая величиной усдв, которая для реальных размеров шпинделей, имеющих центральное отверстие, не превышает 3 -6 %, можем записать
(2.4)
где Е — модуль упругости материала шпинделя; Jx и J2 — осевые моменты инерции сечения шпинделя соответственно на консольной части и между опорами; сх = 1/jx и с2 = 1/j2 — соответственно податливость передней и задней опор шпинделя, которые определяют по реакциям Rx и R2 и перемещениям δJ и δ2 в соответствующих опорах; j1 и j2 — жесткость опор; ξ3 — коэффициент, учитывающий наличие в передней опоре защемляющего момента, если в ней расположено несколько рядов тел качения. Для конструктивных схем, представленных на рис. 1 значения коэффициента ξ3 можно принимать равными 0,65—0,75 (для схемы 1); 0,45—0,65 (для схемы 2); 0,30—0,45 (для схем 3—4); 0,20— 0,30 (для схемы 5); 0,1—0,2 (для схем 6—8); 0 (для схем 9—10). Для гидростатических опор ξ3 равно нулю. В соответствии с формулой (2.4) общая податливость шпиндельного узла имеет вид
(3.4)
где j∑ — суммарная жесткость шпиндельного узла, может быть представлена в виде
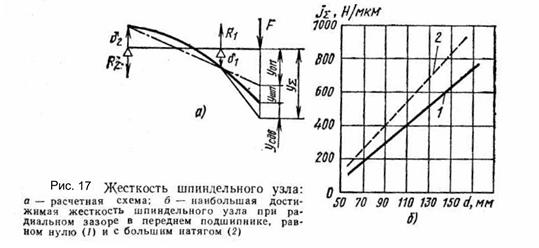
Учитывая, что величины с1, с2, J1 и J2 зависят только от диаметральных размеров шпинделя, можно получить для конкретной конструктивной схемы узла зависимости j∑ = f(d) (рис. 17,б), позволяющие определить диаметр при заданной жесткости шпиндельного узла. При этом надо учитывать конструктивные ограничения, связанные с тем, что d ≤ d1, где d1 — диаметр последней ступени стандартного переднего конца шпинделя, и ограничения по предельной быстроходности подшипников
(5.4) где nmax— максимальная частота вращения шпинделя. После выбора диаметра шейки d можно определить для него оптимальную величину межопорного расстояния loпт, исходя из необходимости получения максимальной жесткости (т. е. минимума суммарной податливости). Для этого используют выражение (4.4) без учета защемления в передней опоре, т. е. при ξ3 = 0. Взяв первую производную с∑ по l и приравняв ее нулю, получим уравнение для определения lопт:
которое легко решается графически. При назначении межопорного расстояния необходимо учитывать его влияние на точность вращения шпинделя. Поэтому обычно в практике станкостроения принято ограничивать возможное значение межопорного расстояния, а именно l ≥ 2,5а. Если учтены все требования к шпиндельному узлу, то можно определить значения главных параметров шпиндельного узла в виде области допустимых значений. На рис. 18 показано построение области допустимых значений для шпиндельного узла универсального токарного станка с nmax = 2500 мин-1. При точностных расчетах необходимо знать величину и направление перемещения переднего конца шпинделя с учетом силового воздействия от приводных элементов. Это могут быть зубчатые передачи, расположенные между опорами на расстоянии 11 (см. рис. 16) от передней опоры, либо ременные передачи со шкивом, расположенным на расстоянии /2 от задней опоры. В этом случае учитывают силы резания и силы привода, которые приводят к двум плоскостям (вертикальной и горизонтальной). По известным формулам сопротивления материалов вычисляют прогиб конца шпинделя в каждой плоскости (ув и ус)
Вычисления целесообразно проводить с учетом защемления в передней опоре и конкретной величины натяга средствами вычислительной техники. Выбирая определенным образом угловое расположение элемента и расстояния 11 и /2, можно добиться минимального влияния привода на положение переднего конца шпинделя. При расчете общей жесткости шпиндельного узла необходимо учитывать жесткость конического соединения шпинделя с приспособлением (оправкой, патроном) или хвостиком инструмента, а также жесткость приспособлений и инструмента. Во многих случаях они являются определяющими в общем балансе жесткости. Например, Для соединения хвостовика инструмента с корпусом шпинделя в соответствии с расчетной схемой, приведенной на рис. 19, упругое перемещение при действии силы F приложенной на расстоянии а1 от конца шпинделя,
где δ — смещение на краю конического соединения вследствие контактных деформаций; θ — угол поворота в коническом соединении. Для конусности 7/24, получившей преимущественное распространение в станках с числовым управлением, без учета погрешностей изготовления жесткость, Н/мкм,
(9.4) где D и а1 —см. рис. 19. Погрешности изготовления конического соединения, обусловленные несовпадением углов конусов отверстия и оправки, резко снижают жесткость соединения. Для ее повышения применяют предварительную затяжку осевой силой F0 (величина которой для конуса ISO 50 составляет 15 кН), которая создается специальными зажимными приспособлениями, расположенными во внутренних цилиндрических полостях шпинделя. Податливость патронов и зажимных цанг при обработке коротких прутков в токарных станках составляет 80—90 % податливости всей системы шпиндельного узла. Во фрезерных и расточных станках доминирующими могут являться деформации концевого инструмента.

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
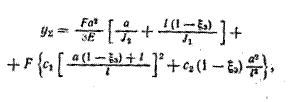
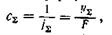
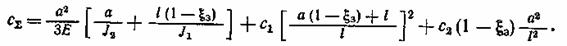 (4.4)
(4.4)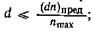
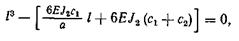 (6.4)
(6.4) (7.4)
(7.4)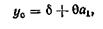 (8.4)
(8.4)