НОРМЫ И СМЫСЛОВОЕ ЗНАЧЕНИЕ ТЕСТОВЫХ ПОКАЗАТЕЛЕЙ

Вторая часть учебника, включающая главы 3-7, знакомит с основными понятиями и методологией, необходимыми для понимания психологических тестов и правильной интерпретации их результатов. Соответственно порядку глав в ней рассмотрены нормы, надежность, валидность, анализ заданий и конструирование тестов. Данная глава посвящена разработке и использованию норм, а также другим процедурам, облегчающим пользователям интерпретацию тестовых показателей. При отсутствии дополнительных интерпретирующих данных первичная оценка по любому психологическому тесту лишена всякого смысла. Сказать, что кто-то верно решил 15 задач в тесте математического рассуждения, правильно опознал 34 слова в словарном тесте или успешно собрал механическую конструкцию за 57 с в тесте технических способностей — значит ничего или почти ничего не сообщить о том, как у этого человека развиты соответствующие функции. Знакомые всем процентные показатели также не дают удовлетворительного решения проблемы интерпретации первичных тестовых оценок. Например, 65 % правильных ответов по одному словарному тесту могут означать то же, что 30 % по другому или 80 % по третьему. Разумеется, процентное выражение показателя может иметь тот или иной смысл в зависимости от трудности заданий, из которых состоит каждый тест. Подобно всем первичным оценкам, процентные показатели могут быть истолкованы только в рамках четко заданной и единой системы отсчета.

Оценки по психологическим тестам чаще всего интерпретируются посредством их сопоставления с нормами, отображающими выполнение теста в выборке стандартизации. Такие нормы устанавливаются эмпирически, путем определения того, как представители репрезентативной группы в действительности справляются с тестом. После чего первичную оценку («сырой» балл) конкретного человека можно соотнести с распределением оценок, полученных на выборке стандартизации, чтобы узнать, какое место он занимает в этом распределении. Соответствует ли его показатель среднему результату группы, на которой проводилась стандартизация теста? Или же он несколько ниже среднего? А может быть, он попадает в верхний конец распределения и, таким образом, намного превосходит средний результат?

Чтобы более точно определить положение индивидуума относительно выборки стандартизации, его «сырой» балл (первичная оценка) переводится в некую относи-

Глава 3- Нормы и смысловое значение тестовых показателей 65

тельную меру. Предполагается, что эти производные оценки должны слу_жИТЬ двум целям. Во-первых, они указывают относительное положение обследован] _1оГО человека в нормативной выборке и позволяют оценить полученный им результат в сравнении с результатами других людей. Во-вторых, они обеспечивают сопоставимые меры, допускающие прямое сравнение выполнения индивидуумом различных тестов. Например, если девочка получила 40 баллов по словарному тесту и 22 балла по тесту арифметического рассуждения, то это ничего не говорит нам о ее относительной результативности по этим двум тестам. Какой тест она выполнила лучше — словарный или арифметический — или оба одинаково хорошо? Поскольку первичные оценки по разным тестам обычно выражаются в разных единицах, прямое сравнение таких оценок невозможно. Различие в степени трудности еще больше усложняет сравнение первичных оценок по соответствующим тестам. Производные же оценки могут быть выражены в одних и тех же единицах и относиться к одним и тем же или весьма сходным нормативным выборкам для различных тестов. Таким образом, оказывается возможным сравнение относительной эффективности индивидуума при выгю_{лнении им} множества разных функций.

Есть различные способы преобразования первичных оценок, с тем чтобы они могли служить двум сформулированным выше целям. Однако, с принципиальной точки зрения, получаемые в результате производные оценки выражают один из двух основных аспектов: 1) достигнутый уровень развития или 2) относительное положение индивидуума в определенной группе. Оба типа оценок и некоторые из их распространенных вариантов будут рассмотрены в специальных разделах этой главы. Но прежде необходимо разобраться с несколькими статистическими понятиями, лежащими в основе разработки и использования норм. Цель следующего раздела — разъяснить смысл традиционных статистических мер. Упрощенные вычислительные примеры приведены в нем лишь для иллюстрации и не предназначены для обучения статистическим методам. С формальной стороной вычислений и конкретными алгоритмами решения прикладных задач читатель может ознакомиться по любому современному учебнику статистики для психологов (см., напр.: D. С. Howell, 1997; Runyon, & Haber, 1991; West, 1991). В настоящее время отмечается растущее осознание потребности в элементарных знаниях статистической методологии, причем это касается не только пользователей тестов, но и всех тех, кто хочет с пониманием читать публикуемые материалы исследований в любой области психологии (L. S. Aiken, West, Sechrest,, & Reno, 1990; Anastasi, 1991; Lambert, 1991; S. T. Meier, 1993).

Статистические понятия

Главная цель статистического метода — представить количественные данные в систематизированной и сжатой форме с тем, чтобы облегчить их понимание. Колонка из 1000 тестовых оценок может выглядеть весьма внушительно, но в таком виде она мало что говорит. В качестве первого шага при наведении порядка в этом хаосе «сырых» баллов можно составить таблицу их частотного распределения (см. табл. 3-1). Для этого сначала определяются — исходя из числовых значений первичных оценок — удобные интервалы группирования, а затем каждая из этих оценок отмечается условным значком (палочкой, крестиком и т. п.) в соответствующем ей интервале. Когда все первичные оценки разнесены по интервалам группирования, в них подсчитывает-

Часть 2. Технические и методологические принципы

ся количество условных значков, с тем чтобы найти частоту, или число случаев, для каждого интервала. Сумма всех частот равняется N— общему числу случаев в данной группе. В табл. 3-1 приведены первичные оценки 1000 студентов по тесту усвоения кода, в котором нужно было перейти от использования искусственных слов или бессмысленных слогов из одного набора к пользованию аналогичными элементами из другого набора. Первичные оценки, представленные числом правильных элементов слогового кода, замененных в течение двухминутной попытки, колеблются в пределах от 8 до 52. Они были разнесены по интервалам группирования с шириной 4 единицы: от 8-11 до 52-55. Из колонки частот видно, что оценки двух испытуемых находятся в интервале 8-11, трех — в интервале 12-15, и т. д.

Таблица 3-1 Частотное распределение первичных оценок студентов по тесту усвоения кода (N= 1000)

(Из Anastasi, 1934, р. 34)

Информация, содержащаяся в частотном распределении, может быть также представлена графически в виде кривой распределения. На рис. 3-1 данные из табл. 3-1 отображены в графической форме. По горизонтальной оси отложены первичные оценки, представленные границами интервалов группирования, а по вертикальной — частоты, или число случаев, попадающих в каждый интервал. Это график построен двумя способами, в виде гистограммы и полигона (частот), оба из которых достаточно распространены. В гистограмме высота столбца над каждым интервалом группирования соответствует числу испытуемых, попавших по результатам тестирования в соответствующий интервал. В полигоне число испытуемых в каждом интервале группирования указывается точкой, расположенной над серединой интервала на высоте, соответствующей его частоте, а сами точки последовательно соединяются отрезками прямой.

Если не обращать внимание на некоторые нерегулярности, распределение, представленное на рис. 3-1, имеет сходство с колоколообразной нормальной кривой. Математически определенная нормальная кривая изображена на рис. 3-2. Этот тип кривой обладает важными математическими свойствами и лежит в основе многих видов статистического анализа. Для наших целей, однако, достаточно будет отметить лишь некоторые из свойств нормальной кривой. Легко заметить, что согласно нормальному

Глава 3. Нормы и смысловое значение тестовых показателей

Рис. 3-1. Кривые распределения: полигон и гистограмма (по данным табл. 3-1)

закону распределения наибольшее число случаев скапливается вокруг центральной точки кривой и постепенно падает к ее краям. Кривая симметрична и имеет единственный максимум в центре. Большинство распределений человеческих признаков — от роста и веса до способностей и свойств личности — приближаются к нормальной кривой. В общем, чем больше группа, тем ближе эмпирическое распределение к теоретической нормальной кривой.

Далее, совокупность тестовых оценок может быть сжато описана некоторой мерой центральной тенденции. Такая мера дает единственную, наиболее типичную или репрезентативную оценку, характеризующую выполнение теста группой испытуемых, взятой в целом. Самой известной из таких мер является выборочное среднее или, точнее, среднее арифметическое, обозначаемое чаще всего большой буквой М (по первой букве англ. слова mean). Оно находится сложением всех оценок и делением получившейся суммы на число случаев (N). Другой мерой центральной тенденции является мода, или наиболее часто встречающаяся оценка. В частотном распределении мода определяется как середина интервала группирования с максимальной частотой. Например, в табл. 3-1 мода представлена средней точкой интервала 32-35 и равна 33,5. Отметим, что эта величина соответствует самой высокой точке кривой распределения на рис. 3-1. Третья мера центральной тенденции — это медиана, или оценка, приходящаяся на середину совокупности ранжированных (упорядоченных по величине) оценок испытуемых. Медиана есть точка, делящая построенное на такой ранжированной совокупности распределение ровно пополам, в результате чего одна половина случаев лежит выше, а другая ниже медианы.

68 Часть 2. Технические и методологические принципы

Рис. 3—2. Частотные распределения с одинаковым средним и разным диапазоном изменчивости

Дополнительную информацию о совокупности тестовых оценок дают меры изменчивости, показывающие степень индивидуальных отклонений от центральной тенденции. Наиболее очевидным и понятным способом представления изменчивости служит размах, определяемый, в простейшем случае, как разность между максимальной и минимальной оценками в совокупности. Однако размах является крайне грубой и неустойчивой мерой изменчивости, поскольку определяется только по двум оценкам. Всего один необычно высокий или низкий результат может заметно повлиять на величину размаха. Более точный метод измерения изменчивости основан на учете разностей между оценками каждого испытуемого и среднегрупповой оценкой.

В этом месте полезно обратиться к примеру в табл. 3-2, где приведены расчеты рассматриваемых нами различных мер для совокупности из 10 случаев. Столь малая совокупность взята для того, чтобы сделать наш пример предельно понятным за счет упрощения вычислений, хотя на практике обычно приходится иметь дело с гораздо большими совокупностями данных. В табл. 3-2 также вводится ряд принятых в статистике обозначений, которые будут использоваться и в дальнейшем. Первичные оценки по тесту по традиции обозначаются прописной буквой X, а строчная буквах служит для обозначения отклонений каждой индивидуальной оценки от группового среднего. Греческая прописная буква ∑ расшифровывается как сумма. Среднее значение и медиана вычислены по данным, представленным в первой колонке табл. 3-2. Среднее равно 40; медиана равна 40,5 и находится посередине между оценками 40 и 41: пять случаев (50 %) лежат выше и пять ниже медианы. Находить моду для столь малой совокупности лишено всякого смысла, так как составляющие ее случаи не обнаруживают явного скопления вокруг какой-либо из оценок. Формально, однако, мода представлена оценкой 41, поскольку такую оценку получили два человека, тогда как все другие оценки встречаются лишь по одному разу.

Вторая колонка таблицы показывает, насколько каждая оценка отклоняется в ту или другую сторону от среднегрупповой (40). Сумма этих отклонений всегда равна нулю, так как положительные и отрицательные отклонения от среднего обязательно уравновешивают друг друга (+20 - 20 = 0). Отбросив знаки отклонений и усредняя

Глава 3. Нормы и смысловое значение тестовых показателей

о«

Таблица 3-2 Иллюстрация понятий центральной тенденции и изменчивости

Оценка (X) Отклонение (х = Х-М) Квадрат отклонения (х²)

+ 8' + 7 + 3 + 1 + 1 О

-2

-4

-6

Примечание. Символы ∑ и σ в этой таблице — соответственно прописная и строчная греческие буквы «сигма». Во многих статистических работах символом SD (или просто 5) обозначается выборочное стандартное отклонение, вычисляемое на основе фактически полученных данных, тогда как символ σ используется для обозначения (ожидаемой величины) стандартного отклонения совокупности, из которой извлекалась выборка для сбора данных.

их абсолютные значения, мы можем получить меру средней величины, на которую каждый человек отклоняется от центральной тенденции группы (выраженной средним арифметическим). Несмотря на некоторые достоинства (прежде всего, ясность и понятность) такой дескриптивной меры, «среднее отклонение» не пригодно для более сложного математического анализа данных из-за произвольного отбрасывания знаков и практически не используется в наше время.

Гораздо более полезной мерой изменчивости является стандартное отклонение (SD или σ), при вычислении которого отрицательные знаки отклонений устраняются математически допустимым способом — путем возведения каждого отклонения в квадрат, как показано в третьей колонке табл. 3-2. Сумма значений в этой колонке,

Деленная на число случаевназывается дисперсией, или средним квадратом от-

клонений. Дисперсия оказалась крайне полезной при выяснении вкладов разных факторов в индивидуальные различия результатов тестирования. Однако в данный мо-

Часть 2. Технические И методологические принципы

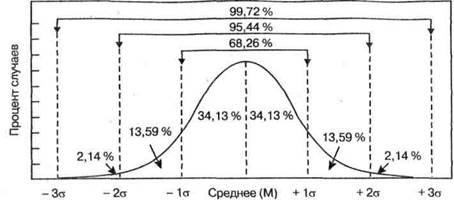
Рис. 3-3. Процентное распределение случаев под нормальной кривой

мент главный интерес для нас представляет стандартное отклонение (SD)\ равное корню квадратному из дисперсии, как видно из табл. 3-2. Эта мера широко используется при сравнении изменчивости данных, полученных в разных группах. На рис. 3-2, например, показаны два распределения с одинаковым средним, но разным диапазоном изменчивости. Распределение с более широким диапазоном индивидуальных различий дает большую величину SD, чем распределение с менее выраженными индивидуальными различиями. При оценивании относительных результатов тестирования двух групп мы должны сравнивать не только средние, но и стандартные отклонения. Если эти группы различаются по диапазону изменчивости оценок, это может указывать на различия в доле высоких, низких или тех и других оценок, независимо от различия средних. Современная статистика располагает комплексными методами анализа эффектов, вызванных различиями средних и стандартных отклонений (см., например, Feingold, 1955).

Как будет показано в разделе о стандартных показателях, SD также выполняет функцию базисного элемента для выражения оценок индивидуума по различным тестам в единицах норм. Интерпретация стандартного отклонения становится особенно ясной в тех случаях, когда речь идет о нормальной или приблизительно нормальной кривой распределения. При нормальном распределении имеется точное соотношение между SD и относительным количеством случаев, как хорошо видно на рис. 3-3. Базис нормальной кривой (ось абсцисс) размечен отрезками, представляющими одно, два и три стандартных отклонения выше и ниже среднего М. Например, для данных, приведенных в табл. 3-2, М = 40 + 1σ = 44,9 (т. е. 40 + 4,9); + 2 σ = 49,8 (т. е. 40 + 2 х 4,9) и т. д. Процент случаев, попадающих в интервал между Ми + 1 σ, для нормального распределения равен 34,13 %. Поскольку кривая симметрична, 34,13 %

¹ Иллюстрируемые в этой главе вычисления относятся к описательной статистике, применяемой к фактически обследованной выборке; в статистике вывода N заменяется на N-1 для того, чтобы получить оценку соответствующих параметров совокупности по выборочным данным. Чем меньше выборка, тем больше будут различия между параметрами генеральной совокупности и их выборочными оценками. За разъяснениями можно обратиться к любому современному учебнику статистики (например, Comrey & Lee, 1992).

Глава 3. Нормы и смысловое значение тестовых показателей

/1

случаев попадает также в интервал между М и — 1 с, так что диапазон от — 1а + 1а хватывает 68,26 % случаев. Почти все случаи (99,72 %) лежат в пределах ± За от среднего (М). Эти соотношения имеют особое значение для интерпретации обсуждаемых чуть позднее стандартных показателей и процентилей.

Возрастные нормы

Один из способов придать смысл тестовым оценкам — это указать, как далеко продвинулся индивидуум по нормальной траектории развития. Так, можно сказать, что 1-летний ребенок, справляющийся с заданиями теста интеллекта на уровне среднего 10-летнего ребенка, имеет умственный возраст (УВ) 10 лет. Умственно отсталый взрослый, выполняющий задания этого теста на том же уровне, будет также иметь УВ = 10 лет. В другом контексте четвероклассника, например, можно охарактеризовать как достигшего нормы 6-го класса по тесту чтения и нормы 3-го класса по арифметическому тесту. В некоторых системах для описания возрастного развития используются более качественные характеристики изменения специфических функций, таких как сенсомоториая активность или формирование понятий. Но независимо от способа выражения, показатели, основанные на возрастных нормах, довольно грубы и плохо поддаются точной статистической обработке. Тем не менее они имеют сильную притягательность в силу своей наглядности и широко используются, особенно при клиническом обследовании, а также при решении ряда научных проблем.

Умственный возраст.Как отмечалось в главе 2, термин «умственный возраст» получил широкое распространение благодаря различным переводам и адаптациям шкал Бине—Симона, хотя сам Вине пользовался более нейтральным термином «умственный уровень». В таких возрастных шкалах, как шкачы Бине и их последующие редакции (до 1986 г.), тестовые задания группируются по возрастным уровням. Например, задания, посильные для большинства 7 -летних детей в выборке стандартизации, относятся к уровню 7 лет; задания, выполняемые большинством 8-летних детей, — к уровню 8 лет и т. д. Казалось бы, в этом случае показатель ребенка по данному тесту должен соответствовать самому высокому возрастному уровню, который ему удалось успешно пройти. В действительности, однако, индивидуальные результаты выполнения теста всегда обнаруживают известную степень разброса. Иными словами, обследуемый может не справиться с некоторыми тестами ниже его умственного возраста и выполнить задания, рассчитанные на более высокий умственный возраст. По этой причине сложилась практика, когда сначала определялся базисный возраст обследуемого, т. е. максимальный возрастной уровень, на котором и ниже которого все тесты оказываются доступными ребенку. А за все тесты, пройденные на более высоких возрастных уровнях, производились «частичные зачеты» — в месяцах, добавляемых к базисному возрасту. В этом случае умственный возраст ребенка по такому тесту представлял собой сумму базисного возраста и дополнительных «зачетных месяцев».

Нормы в форме умственного возраста использовались и при работе с тестами, которые не подразделялись на возрастные уровни. В таком случае сначала определяется первичная оценка ребенка по тесту (так называемый «сырой» балл). В качестве первичной оценки может выступать просто суммарное количество правильно выполненных заданий всего теста, либо она может быть более сложной и строиться с учетом

Часть 2. Технические и методологические принципы

времени выполнения заданий, числа ошибок или даже какой-то комбинации таких мер. Средние величины первичных оценок, полученных детьми в каждой возрастной группе выборки стандартизации, и составляют возрастные нормы для такого теста. Например, средняя первичная оценка 8-летних детей могла бы служить нормой для возраста 8 лет. Если первичная оценка обследуемого равна средней первичной оценке 8-летних детей, то его У В по данному тесту составляет 8 лет. Все первичные оценки по такому тесту можно преобразовать аналогичным способом, соотнося их с возрастными нормами.

Следует отметить, что единица умственного возраста не остается постоянной и с годами обнаруживает тенденцию к сокращению. Так, ребенок, отстающий в развитии на один год в 4-летнем возрасте, к 12 годам будет отставать примерно на 3 года, т. е. один год умственного роста между 3 и 4 годами равносилен 3 годам роста между 9-м и 12-м годом жизни. Поскольку развитие интеллекта идет быстрее в более ранние годы и постепенно замедляется по мере взросления ребенка, единица УВ соответственно уменьшается. Это соотношение можно сделать более наглядным, если представить себе, что рост ребенка выражается в единицах «ростового возраста» {height age). Разница, в дюймах, между ростовым возрастом 3 и 4 года будет большей, чем между ростовым возрастом 10 и 11 лет. В силу постепенного сокращения единицы У В один год опережения или задержки развития в возрасте, скажем, 5 лет означает большее отклонение от нормы, чем тот же год в возрасте 10лет.

Эквивалентные классы.Показатели тестов достижений в обучении часто интерпретируются в единицах эквивалентных классов. Эта практика вполне понятна, поскольку эти тесты применяются в школьной обстановке. Характеризовать достижения ученика как соответствующие уровню 7-го класса по орфографии, уровню 8-го класса по чтению и уровню 5-го класса по арифметике, для большинства столь же притягательно, как пользоваться понятием умственного возраста в традиционных тестах интеллекта.

Нормы в виде эквивалентных классов определяются посредством вычисления среднего по первичным оценкам, полученным детьми в каждом классе. Так, если среднее количество правильно решенных задач арифметического теста в выборке стандартизации четвероклассников равно 23, то первичная оценка 23 соответствует эквивалентному 4-му классу. Промежуточные эквивалентные классы, представляющие как бы доли класса, обычно определяются путем интерполяции, хотя их можно получить и непосредственно, тестируя детей несколько раз в учебном году. Поскольку учебный год длится 10 месяцев, их последовательность можно представить в виде шкалы десятых долей эквивалентного класса. Тогда 4,0 будет указывать на средний результат выполнения теста в начале обучения в 4-м классе (сентябрьское тестирование), а 4,5 — на средний результат по тому же тесту в середине обучения (февральское тестирование), и т. д.

Несмотря на их популярность, нормы в виде эквивалентных классов имеют ряд недостатков. Во-первых, содержание обучения меняется от класса к классу. Поэтому такие нормы подходят только для общеобразовательных предметов, обучение которым ведется на всех уровнях, охватываемых данным тестом. Они, как правило, неприменимы в старших классах, где многие предметы изучают только один или два года. Даже если предмет преподается на протяжении всего обучения в школе, его значение

Глава 3. Нормы и смысловое значение тестовых показателей 73

может меняться от класса к классу и, следовательно, скорость его изучения может быть различной. Иными словами, единицы шкалы эквивалентных классов явно не равны друг другу, причем отсутствует определенная закономерность в их изменении для разных предметов.

Кроме того, представленные в виде эквивалентных классов нормы могут приводить к ошибочной интерпретации результатов тестирования, если пользователь теста не принимает в расчет способ их получения. Например, если четвероклассник в шкале эквивалентных классов получил оценку 6,9 по арифметике, то это вовсе не означает, что он овладел арифметическими операциями, которым обучают в 6-м классе. Бесспорно, он показал такой результат главным образом благодаря отличному знанию арифметики, которую проходят в 4-м классе. И конечно, нельзя считать, что он уже готов к ее изучению по программе 7-го класса. Наконец, нормы в виде эквивалентных классов иногда ошибочно трактуют как нормативы выполнения теста. Учительница 6-го класса, например, может решить, что все ее ученики должны иметь в тестах достижений результаты, соответствующие или по крайней мере близкие к норме 6-го класса. Разумеется, это ошибочное представление не редкость, когда используются нормы в виде эквивалентных классов. Однако индивидуальные различия в пределах одного класса таковы, что диапазон оценок по тесту достижения будет обязательно перекрывать несколько эквивалентных классов.

Порядковые шкалы.Еще один подход к нормам возрастного развития берет начало в исследованиях по детской психологии. Благодаря эмпирическим наблюдениям за развитием младенцев и дошкольников был накоплен обширный материал, позволяющий описать последовательность типичных возрастных изменений таких функций, как локомоция, сенсорное различение, речевое общение и формирование понятий. В качестве первого из таких исследований можно назвать работу А. Гезелла и его коллег по Йельскому университету (Ames, 1937; Gesell, & Amatruda, 1947; Halverson, 1933; Knobloch, & Pasamanick, 1974). «Таблицы развития» Гезелла (GesellDevelopmental Schedules) позволяют оценить приблизительный уровень развития в месяцах, которого ребенок достиг в каждой из четырех основных областей поведения, именно: двигательного, речевого, приспособительного и лично-социального поведения. Эти уровни определяются сравнением поведения конкретного ребенка с типичным поведением детей в восьми поворотных точках графика возрастного развития, охватывающего диапазон от 4 недель до 36 месяцев.

Гезелл и его сотрудники особо подчеркивали последовательный характер раннего развития поведения. Они приводили обширные данные, свидетельствующие о единообразии хода развития и организации изменений поведения в четкие последовательности. Например, реакции ребенка на помещенный перед ним небольшой предмет обнаруживают характерную хронологическую последовательность в зрительной фиксации и в движениях руки и пальцев. Попытки захватить предмет всей ладонью предшествуют захвату с помощью большого пальца, противопоставляемого остальным четырем, а он, в свою очередь, сменяется более эффективным пинцетным захватом, когда ребенок зажимает предмет между большим и указательным пальцем. Аналогичные последовательные структуры обнаруживаются также в развитии ходьбы, подъеме по лестнице и в большей части сенсомоторного развития первых лет жизни. Шкалы, разработанные в рамках этого подхода, являются порядковыми в том смысле, что смена ста-

Часть 2. Технические и методологические принципы

дни развития следует неизменному порядку, причем каждая новая стадия предполагает предварительное усвоение поведения, характерного для предыдущих стадий.¹

В 1960-х гг. резко возрос интерес к теориям развития швейцарского детского психолога Жана Пиаже (см. Flevell, 1963; Ginsburg, & Оррег, 1969; D. R. Green, Ford, & Flamer, 1971). Исследования Ж. Пиаже были сосредоточены на развитии когнитивных процессов от младенчества до старшего подросткового возраста. Его больше интересовало развитие специфических понятий, нежели способностей в широком смысле слова. Примером такого понятия, или схемы, может служить постоянство объекта, благодаря которому ребенок сознает тождественность и непрерывность существования объектов, когда они видны под разными углами или находится вне поля зрения. Другим широко изученным понятием является сохранение, т. е. сознавание того, что то или иное свойство объекта сохраняется неизменным, несмотря на воспринимаемые преобразования объекта, как в случаях, когда одно и то же количество жидкости наливается в сосуды разной формы или когда палочки одинаковой длины по-разному располагаются в пространстве.

Задачи Пиаже широко использовали психологи, изучающие возрастное развитие, а некоторые из его задач были организованы в стандартизованные шкалы, которые будут обсуждаться в главе 9 (Goldschmid, & Bentler, 1968b; Pinard, & Laurendeau, 1964; Uzgiris, & Hunt, 1975). В соответствии с подходом Пиаже, эти инструменты являются шкалами порядка, в которых достижение той или иной стадии зависит от успешного прохождения более ранних стадий развития измеряемого понятия. Задания в этих шкалах конструируются таким образом, чтобы выявлять главные аспекты каждой стадии развития; и только затем собираются эмпирические данные о возрасте, в котором обычно достигается каждая стадия. В этом отношении данная процедура отличается от процедур, применяемых при построении возрастных шкал, в которых задания отбираются прежде всего по их способности дифференцировать смежные возрасты. Хотя интерес к вкладам школы Пиаже в диагностику психического развития сохраняется, критический теоретический анализ и многочисленные эмпирические проверки этого подхода высветили как его конструктивность, так и ряд ограничений (Sugarman, 1987).²

Подводя итог, можно сказать, что порядковые шкалы предназначены для определения стадии, достигаемой ребенком в развитии специфических функций поведения. Хотя получаемые по ним оценки могут сообщаться в виде указания примерных возрастных уровней, такая форма оценок имеет второстепенное значение по сравнению с качественным описанием типичного поведения обследуемого ребенка. Слово «порядок», входящее в название данного типа шкал, указывает на существование единообразия в развитии, проходящем через последовательные стадии. Поскольку эти шкалы обычно дают информацию о том, что конкретный ребенок способен делать в настоя-

¹ Данное значение термина «порядковая шкала» отличается от принятого в статистике, где он обозначает любую шкалу, позволяющую упорядочивать различающиеся объекты (или людей) без знания величины различий между ними. В статистическом смысле шкалы порядка противопоставляются шкалам равных интервалов, имеющим единицы измерения. Порядковые шкалы развития ребенка фактически конструируются но образцу шкалы Гуттмана, или модели симплекса, в которой успешное выполнение заданий на одном уровне автоматически предполагает достижение успеха на всех более низких уровнях (L. Guttman, 1944). Расширение анализа Гуттмана с целью включения в пето нелинейных иерархий описано у Bart и Airasian (1974), со специальными ссылками па шкалы Пиаже.

² Что касается более подробной оценки пиажетианского подхода, см. главу 9.

Глава 3. Нормы и смысловое значение тестовых показателей

щее время (например, взобраться по лестнице без посторонней помощи или понять, что количество жидкости сохраняется неизменным при переливании ее в сосуды разной формы), они обладают теми же существенными признаками, что и предметно-ориентированные тесты (domain-referenced tests), обсуждаемые в одном из последующих разделов этой главы.

Внутригрупповые нориы

В наше время почти все стандартизованные тесты предусматривают ту или иную форму внутригрупповых норм (within-group norms). При наличии таких норм индивидуальный результат тестирования оценивается исходя из выполнения данного теста в наиболее сопоставимой группе стандартизации, как при сравнении полученной ребенком первичной оценки с первичными оценками детей того же возраста или того же года обучения. Внутригрупповые показатели имеют единый и четко определенный количественный смысл и допускают корректное применение большинства методов статистического анализа.

Процентили.Процентильные показатели выражаются в единицах процента лиц, составляющих выборку стандартизации, результат которых ниже установленной первичной оценки. Например, если 28 % людей решают правильно меньше 15 задач в тесте арифметического рассуждения, то первичная («сырая») оценка 15 соответствует 28-му процентилю (Р₂₈). Процентиль показывает относительное положение индивидуума в выборке стандартизации. Процентили можно также рассматривать как ранга в группе из 100, с той лишь разницей, что при ранжировании принято начинать отсчет сверху, т. е. с лучшего члена группы, получающего ранг 1. Напротив, в случае процентилей отсчет ведется снизу, так что чем ниже процентиль, тем хуже позиция индивидуума.

50-й процентиль (Р ) соответствует медиане — одной из рассмотренных выше мер центральной тенденции. Процентили выше 50-го представляют результаты выше среднего, а процентили ниже 50-го указывают на низкие результаты. 25-й и 75-й процентили называют также 1-ми 3-м квартилями (Q₁ и Q₃), поскольку они отсекают нижнюю и верхнюю четверти распределения. Как и медиана, они служат удобными ориентирами для описания распределения показателей и его сравнения с другими распределениями.

Процентили не следует смешивать с привычными для всех процентными показателями. Последние являются первичными оценками и выражаются в единицах процента правильно выполненных заданий, тогда как процентили — это производные оценки, выражающиеся в единицах процента тестируемых. Первичная оценка ниже любой полученной в выборке стандартизации имела бы процентиль, равный нулю (Р_д), тогда как первичная оценка, превышающая любую оценку в выборке стандартизации, получила бы процентиль 100 (Р,₀₀). Эти процентили, однако, вовсе не означают нулевого или абсолютного результата выполнения теста.

Процентильные показатели обладают рядом достоинств. Их легко рассчитать и Понять даже сравнительно неподготовленному человеку. Кроме того, процентили имеют универсальное применение. Они в равной мере используются при работе как с Детьми, так и со взрослыми, и подходят к любому типу теста, независимо от того измеряет ли он способности или свойства личности.

Часть 2. Технические и методологические принципы

Не нашли, что искали? Воспользуйтесь поиском по сайту: