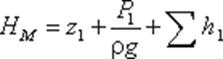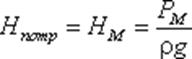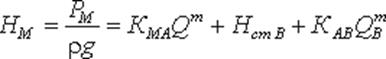|
|
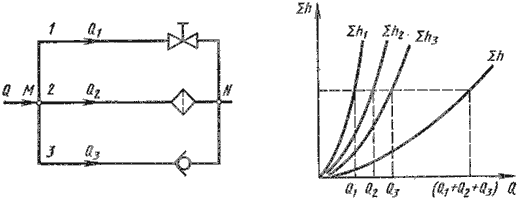
Параллельное соединение трубопроводовТакое соединение нескольких простых трубопроводов, например, 1, 2 и 3 между точками M и N показано на рисунке (74). Параллельное соединение трубопроводов имеет две общие точки: M, в этой точке трубопроводы размыкаются и N, в этой точке трубопроводы соединяются вновь
Рисунок 74 — Параллельное соединение трубопроводов Очевидно, что выполняется следующее равенство:
В точках M и N установлено по пьезометру. Так избыточное давление в точке M — РМ, то жидкость в пьезометре, установленном в этой точке, под действием этого давления поднимется на высоту Потери напора в трубопроводах 1, 2 и 3 соответственно:
Отсюда делаем следующий важный вывод:
то есть потери напора в параллельных трубопроводах равны между собой. Их можно выразить в общем виде через соответствующие расходы следующим образом
Следовательно, в дополнение к уравнению (110) получаем на основании равенств (102), (103) ещё два уравнения:
То есть для параллельного соединения трубопроводов, состоящего из трёх ветвей, получили систему трёх уравнений (101), (104), из которой можно найти три неизвестных, например, расходы в параллельных ветвях Q1, Q2, Q3, а затем и общий расход Q по уравнению (104). Таким образом, для параллельного соединения трубопроводов, состоящего из n ветвей, составляется n уравнений, одно из которых для расходов, и n – 1 для потерь напора. Из уравнений (100) и (104)вытекает следующее важное правило: для построения характеристики параллельного соединения нескольких трубопроводов следует сложить абсциссы (расходы) характеристик этих трубопроводов при одинаковых ординатах (потерях напора). Пример такого построения приведён на рисунке 74.
8.8 Разветвленное соединение.
Разветвленным соединением называется совокупность нескольких простых трубопроводов, имеющих одно общее сечение - место разветвления (или смыкания) труб.
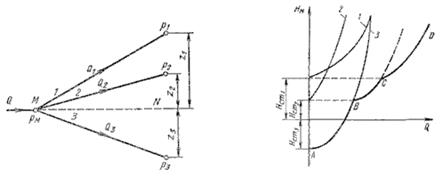
Рис. 75. Разветвленный трубопровод
Пусть основной трубопровод имеет разветвление в сечении М-М, от которого отходят, например, три трубы 1, 2 и 3 разных диаметров, содержащие различные местные сопротивления (рис. 75, а). Геометрические высоты z1, z2 и z3 конечных сечений и давления P1, P2 и P3 в них будут также различны. Так же как и для параллельных трубопроводов, общий расход в основном трубопроводе будет равен сумме расходов в каждом трубопроводе: Q = Q1 + Q2 + Q3 Записав уравнение Бернулли для сечения М-М и конечного сечения, например первого трубопровода, получим (пренебрегая разностью скоростных высот):
Обозначив сумму первых двух членов через Hст и выражая третий член через расход, получаем HM = Hст 1 + KQ1m Аналогично для двух других трубопроводов можно записать HM = Hст 2 + KQ2m HM = Hст 3 + KQ3m Таким образом, получаем систему четырех уравнений с четырьмя неизвестными: Q1, Q2 и Q3 и HM. Построение кривой потребного напора для разветвленного трубопровода выполняется сложением кривых потребных напоров для ветвей по правилу сложения характеристик параллельных трубопроводов (рис. 75, б) - сложением абсцисс (Q) при одинаковых ординатах (HM). Кривые потребных напоров для ветвей отмечены цифрами 1, 2 и 3 , а суммарная кривая потребного напора для всего разветвления обозначена буквами ABCD. Из графика видно, что условием подачи жидкости во все ветви является неравенство HM > Hст1.
Сложные трубопроводы
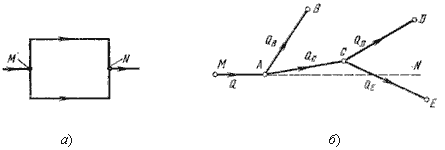
Сложный трубопровод в общем случае составлен из простых трубопроводов с последовательным и параллельным их соединением (рис. 76, а) или с разветвлениями (рис. 76, б).
Рис. 76. Схемы сложных трубопроводов
Рассмотрим разомкнутый сложный трубопровод (рис. 76, б). магистральный трубопровод разветвляется в точках А и С. Жидкость подается к точкам (сечениям) B, D и E с расходами Q B и QD и QE . Пусть известны размеры магистралей и всех ветвей (простых трубопроводов), заданы все местные сопротивления, а также геометрические высоты конечных точек, отсчитываемые от плоскости M - N и избыточные давления в конечных точках PB и PD и PE. Для этого случая возможны два вида задач: Задача 1. Дан расход Q в основной магистрали MA. Необходимо определить расходы QB и QD и QE, а также потребный напор в точке М.
Задача 2. Дан напор в точке М. Определить расход в магистрали Q и расходы в каждой ветви. Обе задачи решают на основе одной и той же системы уравнений, число которых на единицу больше числа конечных ветвей, а именно: уравнение расходов: Q = QB = QD = QE уравнение равенства потребных напоров для ветвей CD и CE Hст D + KCDQDт = Hст E + KCEQEт уравнение равенства потребных напоров для ветви АВ и сложного трубопровода АСЕD Hст B + KABQBт = Hст D + KCDQDт + KAC(QD + QE)т выражение для потребного напора в точке М
Расчет сложных трубопроводов часто выполняют графоаналитическим способом, т.е. с применением кривых потребного напора и характеристик трубопроводов. Кривую потребного напора для сложного трубопровода следует строить следующим образом: 1) сложный трубопровод разбивают на ряд простых; 2) строят кривые потребных напоров для каждого из простых трубопроводов; 3) складывают кривые потребных напоров для ветвей (и параллельных линий, если они имеются) по правилу сложения характеристик параллельных трубопроводов; 4) полученную кривую складывают с характеристикой последовательно присоединенного трубопровода по соответствующему правилу. Таким образом, при расчете идут от конечных точек трубопровода к начальной точке, т.е. против течения жидкости. Сложный кольцевой трубопровод. Представляет собой систему смежных замкнутых контуров, с отбором жидкости в узловых точках или с непрерывной раздачей жидкости на отдельных участках (рис. 77).
Рис. 77. Схема сложного кольцевого трубопровода
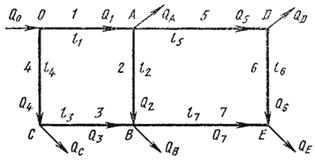
Задачи для таких трубопроводов решают аналогичным методом с применением электроаналогий (закон Кирхгофа). При этом основываются на двух обязательных условиях. Первое условие - баланс расходов, т.е. равенство притока и оттока жидкости для каждой узловой точки. Второе условие - баланс напоров, т.е. равенство нулю алгебраической суммы потерь напора для каждого кольца (контура) при подсчете по направлению движения часовой стрелки или против нее. Для расчета таких трубопроводов типичной является следующая задача. Дан максимальный напор в начальной точке, т.е. в точке 0, минимальный напор в наиболее удаленной точке Е, расходы во всех шести узлах и длины семи участков. Требуется определить диаметры трубопроводов на всех участках.

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
 (100)
(100) ; избыточное давление в точке N — РN, поэтому жидкость в пьезометре, установленном в этой точке, под действием этого давления поднимется на высоту
; избыточное давление в точке N — РN, поэтому жидкость в пьезометре, установленном в этой точке, под действием этого давления поднимется на высоту 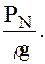
 (101)
(101) (102)
(102) (103)
(103) (104)
(104)