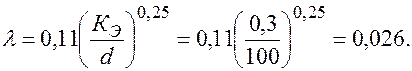|
|
Тема 8 Гидравлический расчет трубопроводовТрубопроводы служат руслами, по которым перекачиваются жидкости. Жидкость движется по трубопроводу потому, что её энергия в начале трубопровода больше, чем в конце. Этот перепад энергий создаётся, как правило, насосом, а иногда за счёт разности высот начала и конца трубы. В горной промышленности приходится иметь дело, главным образом, с такими трубопроводами, движение жидкости в которых обусловлено работой насосов. При расчетах напорных трубопроводов основной задачей является либо определение пропускной способности (расхода), либо потери напора на том или ином участке, равно как и на всей длине, либо диаметра трубопровода на заданных расходе и потерях напора. В практике трубопроводы делятся на короткие и длинные. К первым относятся все трубопроводы, в которых местные потери напора превышают 5…10% потерь напора по длине. При расчетах таких трубопроводов обязательно учитывают потери напора в местных сопротивлениях. К ним относят, к примеру, маслопроводы объемных передач. Ко вторым относятся трубопроводы, в которых местные потери меньше 5…10% потерь напора по длине. Их расчет ведется без учета местных потерь. К таким трубопроводам относятся, например, магистральные водоводы, нефтепроводы. Учитывая гидравлическую схему работы длинных трубопроводов, их можно разделить также на простые и сложные. Простыми называются последовательно соединенные трубопроводы одного или различных сечений, не имеющих никаких ответвлений. К сложным трубопроводам относятся системы труб с одним или несколькими ответвлениями, параллельными ветвями и т.д. К сложным относятся и так называемые кольцевые трубопроводы.
Классификация трубопроводов 1) По материалу стенок трубтрубопроводы бывают стальные, чугунные, железобетонные, пластмассовые, асбестоцементные, резиновые шланги и т.д. 2) По роду перекачиваемой жидкости— водопроводы, нефтепроводы, маслопроводы и т.д. 3) По конфигурации: а) простые— это трубопроводы, не имеющие ответвлений; б) сложные — это трубопроводы, имеющие хотя бы одно ответвление.
Простой трубопровод постоянного сечения
Пусть простой трубопровод постоянного сечения расположен произвольно в пространстве (рисунок 69), имеет общую длину Скорость потока в этих сечениях вследствие постоянства диаметра трубы одинакова и равна u. Запишем уравнение Бернулли для сечений 1— 1и 2— 2, считая a1 = a2 = 1 (как при турбулентном режиме) и исключая скоростные напоры вследствие равенства скоростей:
Пьезометрическую высоту, стоящую в левой части уравнения (91) назовем потребным напором
разность высот начала и конца трубопровода обозначим
Тогда уравнение (91):
Учитывая, что полные потери напора в виде степенной функции расхода можно записать в виде
равенство (92) можно записать:
где Формулы (92) и (93) являются основными для расчёта простых трубопроводов постоянного сечения.
Самотечный трубопровод Самотечный трубопровод — это такой простой трубопровод постоянного сечения, движение жидкости по которому происходит лишь за счёт разности высот начала и конца трубопровода(рис. 70).
Для простого трубопровода постоянного сечения справедливо ранее полученное равенство (92):
В данном случае
Тогда равенство (94) примет вид:
или после сокращения
по этому равенству рассчитывается самотечный трубопровод, оно показывает, что весь имеющийся напор Учитывая, что
откуда расход жидкости в самотечном трубопроводе:
где а — сопротивление трубопровода, рассчитывается по полученной выше по формуле:
Сифонный трубопровод Сифонный трубопровод — это такой простой трубопровод постоянного сечения, часть которого расположена выше питающего его резервуара (рисунок 71).
Для того чтобы сифонный трубопровод начал работать, необходимо его заполнить жидкостью, удалив воздух. Этого можно достигнуть путем повышения временно уровня резервуара (или давления в начале трубы) выше наивысшей точки сифона (уровня z)или путем отсасывания воздуха из сифона в наивысшей точке, благодаря чему под атмосферным давлением на уровнях I — I и II — II трубопровод заполнится жидкостью. Наконец, можно запереть концы сифона и залить его жидкостью через верхнюю точку, где одновременно выпускают заполнявший трубу воздух. После сплошного заполнения сифона жидкостью он начинает работать как обыкновенная труба. Расчетом обычно определяют пропускную способность сифона и предельное значение высоты z. Так как сифонный трубопровод — это простой трубопровод постоянного сечения, то для него справедлива формула (93):
Проанализируем эту формулу для сечений I — I и III — III (плоскость сравнения проходит по сечению III — III):
Тогда формула (96) примет вид:
или после сокращений
откуда найдётся расход Q по сифонному трубопроводу:
где а — сопротивление трубопровода, рассчитывается по полученной выше по формуле:
Для определения высоты z, на которую может подняться жидкость в сифонном трубопроводе, составим уравнение Бернулли для сечений I — I и II — II:
Если плоскость сравнения 0 — 0, совпадает с поверхностью жидкости в резервуаре 1, то z1 = 0; Р1 = Ра; u1 » 0; aI = aII = 1 (принимаем режим движения жидкости турбулентным); zII = z; рII > pн.п. — давление в сечении II — II должно быть больше давления насыщенных паров жидкости pн.п. — давления, при котором жидкость закипает при данной температуре, иначе наблюдается явление кавитации — самовскипания жидкости в замкнутом объёме и образующиеся при этом пузырьки пара приводят к срыву работы сифонного трубопровода. Тогда уравнение (97) примет вид:
откуда высота z, на которую может подняться жидкость в сифонном трубопроводе:
Например, для воды: Ра = 10 м вод. ст. тогда:
Таким образом, максимальная высота, на которую может подняться жидкость в сифонном трубопроводе, перекачивающим воду, не превышает 10 м.
Задача. По сифонному трубопроводу длиной Решение.Высотаz найдётся по формуле:
Давление насыщенных паров воды при t = 200С — 0,24 м вод. ст. [Справочник по гидравлическим расчетам / Под ред. П. Г. Киселева, стр.279]. Определяем скорость воды
Число Рейнольдса
Предельные числа Рейнольдса: — первое — второе Так как
Тогда высота, на которую может подняться вода в сифонном трубопроводе

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
 Рисунок 69 — Схема простого трубопровода постоянного сечения
Рисунок 69 — Схема простого трубопровода постоянного сечения
 , диаметр d = сonst и содержит ряд местных сопротивлений, например, задвижку, фильтр и обратный клапан. В начальном сечении 1 — 1 геометрическая высота равна z1 и избыточное давление p1, а в конечном сечении 2— 2 соответственно z2 и р2.
, диаметр d = сonst и содержит ряд местных сопротивлений, например, задвижку, фильтр и обратный клапан. В начальном сечении 1 — 1 геометрическая высота равна z1 и избыточное давление p1, а в конечном сечении 2— 2 соответственно z2 и р2. (91)
(91)
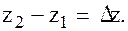
 (92)
(92)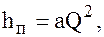
 (93)
(93) сопротивление трубопровода.
сопротивление трубопровода.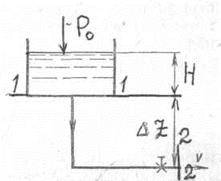 Рисунок 70 — Схема самотечного трубопровода
Рисунок 70 — Схема самотечного трубопровода
 Р2 = Ратм,
Р2 = Ратм,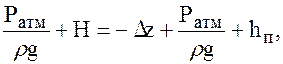
 (95)
(95) идёт на преодоление гидравлических сопротивлений hп.
идёт на преодоление гидравлических сопротивлений hп. равенство (95) запишется:
равенство (95) запишется: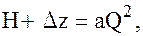
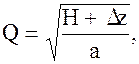
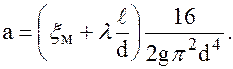
 Рисунок 71 — Схема к гидравлическому расчёту
сифонного трубопровода
Рисунок 71 — Схема к гидравлическому расчёту
сифонного трубопровода
 (96)
(96)

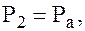
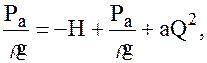
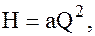
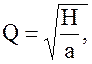
 (97)
(97)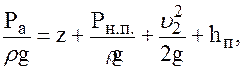
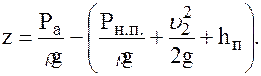
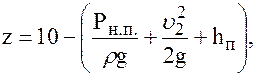
 , диаметром d = 100 мм, КЭ = 0,3 мм, x = 4 переливается вода при t = 200С с расходом Q = 20 л/с. Определить высоту z, на которую может подняться вода в сифонном трубопроводе.
, диаметром d = 100 мм, КЭ = 0,3 мм, x = 4 переливается вода при t = 200С с расходом Q = 20 л/с. Определить высоту z, на которую может подняться вода в сифонном трубопроводе.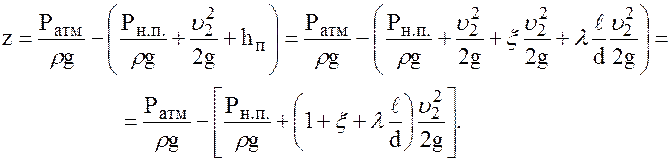
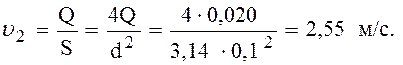
 режим турбулентный.
режим турбулентный.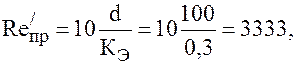
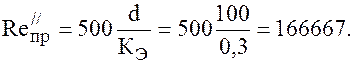
 то зона сопротивления квадратичная, и коэффициент гидравлического трения l определяется по формуле Шифринсона:
то зона сопротивления квадратичная, и коэффициент гидравлического трения l определяется по формуле Шифринсона: