
|
|
Расход, средняя скорость и потери напора при ламинарном течении жидкости в круглой трубе
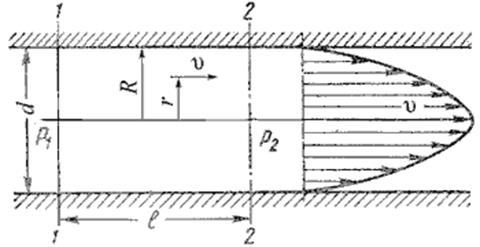
Как показывают исследования, при ламинарном течении жидкости в круглой трубе максимальная скорость находится на оси трубы. У стенок трубы скорость равна нулю, т.к. частицы жидкости покрывают внутреннюю поверхность трубопровода тонким неподвижным слоем. От стенок трубы к ее оси скорости нарастаю плавно. График распределения скоростей по поперечному сечению потока представляет собой параболоид вращения, а сечение параболоида осевой плоскостью - квадратичную параболу (рис.40).
Рис. 40. Схема для рассмотрения ламинарного потока Уравнение, связывающее переменные υ и r, имеет следующий вид:
где P1 и P2 - давления соответственно в сечениях 1 и 2. У стенок трубы величина r = R, значит скорость υ = 0, а при r = 0 (на оси потока) скорость будет максимальной
Теперь определим расход жидкости при ламинарном течении в круглой трубе. Так как эпюра распределения скоростей в круглой трубе имеет вид параболоида вращения с максимальным значением скорости в центре трубы, то расход жидкости численно равен объему этого параболоида. Определим этот объем. Максимальная скорость дает высоту параболоида
Как известно из геометрии, объем параболоида высотой h и площадью ρR2 равен
а в нашем случае
Если вместо R подставить диаметр трубы d, то формула приобретет вид
Расход в трубе можно выразить через среднюю скорость:
откуда
Для определения потерь напора при ламинарном течении жидкости в круглой трубе рассмотрим участок трубы длиной l, по которому поток течет в условиях ламинарного режима (рис.40). Потеря давления в трубопроводе будет равна:
Если в формуле динамический коэффициент вязкости μ заменить через кинематический коэффициент вязкости υ и плотность ρ ( μ = υ ρ ) и разделить обе части равенства на объемный вес жидкости γ = ρ g, то получим:
Так как левая часть полученного равенства равна потерям напора hпот в трубе постоянного диаметра, то окончательно это равенство примет вид:
Уравнение может быть преобразовано в универсальную формулу Вейсбаха-Дарси, которая окончательно записывается так:
где λ - коэффициент гидравлического трения, который для ламинарного потока вычисляется по выражению:
Однако при ламинарном режиме для определения коэффициента гидравлического трения λ Т.М. Башта рекомендует при Re < 2300 применять формулу
Формулу (49) можно также использовать при расчете трубопроводов и открытых русел с любой формой живого сечения потока, если заменить в ней диаметр гидравлическим радиусом.
Задача: По трубе длиной l=100 м; d=100 мм; перекачивается 10 л/с жидкости. Определить потери напора по длине, если n=0,726 см2/с. Решение:
Тема 5 Турбулентное течение жидкости в круглых трубах
Основные сведения Для турбулентного течения характерно перемешивание жидкости, пульсации (мгновенные изменения) скоростей и давлений в разных точках потока жидкости. Если с помощью особо чувствительного прибора-самописца измерить и записать пульсации, например, скорости по времени в фиксированной точке потока, то получим картину, подобную показанной на рисунке 41. Скорость беспорядочно колеблется около некоторого осреднённого uоср по времени значения, которое в данном случае остается постоянным.
Траектории частиц, проходящих через данную неподвижную точку пространства в разные моменты времени, представляют собой кривые линии различной формы, несмотря на прямолинейность трубы. Характер линий тока в трубе в данный момент времени также отличается большим разнообразием (рисунок 42). Таким образом, строго говоря, турбулентное течение всегда является неустановившимся, так как значения скоростей и давлений, а также траектории частиц, изменяются по времени. Однако его можно рассматривать как установившееся течение при условии, что осредненные по времени значения скоростей и давлений, а также полный расход потока не изменяются со временем. Такое течение встречается на практике достаточно часто. Распределение скоростей (осредненных по времени) в поперечном сечении турбулентного потока существенно отличается от того, которое характерно для ламинарного течения. Если сравним кривые распределения скоростей в ламинарном и турбулентном потоках в одной и той же трубе и при одном и том же расходе (одинаковой средней скорости), то обнаружим существенное различие (рисунок 43). Распределение скоростей при турбулентном течении более равномерное, а нарастание скорости у стенки более крутое, чем при ламинарном течении, для которого характерен параболический закон распределения скоростей.
В связи с этим коэффициент Кориолиса a, учитывающий неравномерность распределения скоростей в уравнении Бернулли, при турбулентном течении значительно меньше, нежели при ламинарном. Потери энергии при турбулентном течении жидкости в трубах также получаются иными, нежели при ламинарном. В турбулентном потоке при Re >> Reкр потери напора на трение по длине значительно больше, чем при ламинарном течении при тех же размерах трубы, расходе и вязкости жидкости, а следовательно, при одинаковых числах Re (ламинарный режим при этом неустойчив). Если при ламинарном течении потеря напора на трение возрастает пропорционально скорости (расходу) в первой степени, то при переходе к турбулентному течению заметны некоторый скачок сопротивления и затем более крутое нарастание величины hrpпо кривой, близкой к параболе второй степени (рисунок 43). Ввиду сложности турбулентного течения и трудностей его аналитического исследования до настоящего времени для него не имеется достаточно строгой и точной теории. Существуют полуэмпирические, приближенные теории, например теория Прандтля и другие. В большинстве случаев для практических расчетов, связанных с турбулентным течением жидкостей в трубах, пользуются экспериментальными данными.

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
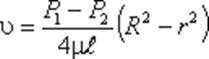
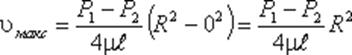
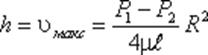
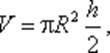
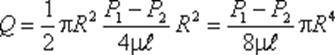
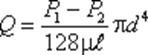
 (53)
(53)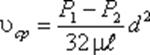
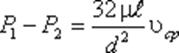
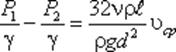
 (54)
(54) (55)
(55)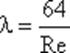
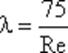
 (56)
(56)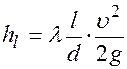
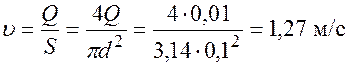
 - ламинарный режим
- ламинарный режим
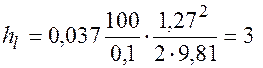 м.
м. Рисунок 41 — Пульсации
скорости в турбулентном
потоке
Рисунок 41 — Пульсации
скорости в турбулентном
потоке
 Рисунок 42 — Характер линий тока в турбулентном потоке
Рисунок 42 — Характер линий тока в турбулентном потоке

 от u и Q
от u и Q