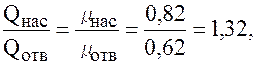|
|
Тема 7 Истечение жидкости через отверстия и насадкиВ инженерной практике часто приходится иметь дело с истечением жидкости через отверстия и насадки различных форм. Истечение жидкости может происходить как в атмосферу (незатопленные отверстия и насадки), так и под уровень (затопленные отверстия и насадки), при постоянном напоре перед отверстием или насадком или при переменном напоре. Основное в этой теме — как определить скорость истечения жидкости через отверстие или насадок, как определить расход.
Истечение жидкости через малое отверстие в тонкой стенке при постоянном напоре Отверстие считается малым, если его диаметр d < 0,1 Н0 (рисунок 51), что позволяет считать давление во всех точках этого отверстия практически одинаковым. Стенка считается тонкой, если её толщина
Наименьшее живое сечение струи (С — С) называется сжатым сечением,его диаметр dС, площадь живого сечения SC. Отношение площади сжатого сечения SC к площади отверстия S называется коэффициентом сжатия струи:
Среднюю скорость u в сжатом сечении струи найдём из уравнения Бернулли для сечений 0 — 0 и С — С:
Если плоскость сравнения проходит по оси отверстия, то z0 = H0; u0 » 0, так как u0 << uC; zC = 0; a0 = aС = 1 (режим, как правило, турбулентный); обозначим скорость в сжатом сечении струи uС = u; полные потери напора, пренебрегая потерями напора по длине, так как ввиду малости толщины стенки
где xМ — коэффициент местного сопротивления отверстия. Тогда уравнение (69) принимает вид:
В равенстве (75) объединим члены:
расчётный напор. Тогда (75):
откуда скорость в сжатом сечении струи
Обозначим
Выясним физический смысл коэффициента скорости истечения j. Для идеальной жидкости коэффициент сопротивления отверстия xМ = 0. Тогда коэффициент скорости истечения для идеальной жидкости
Тогда по формуле (78) скорость истечения идеальной жидкости
Для реальной жидкости из равенства (74)
То есть коэффициент скорости истечения показывает, чему равно отношение действительной скорости истечения через отверстие к теоретической, так как действительная скорость истечения u всегда меньше теоретической скорости истечения uТЕОР, то j < 1. Расход через отверстие
Площадь сжатого сечения струи SС найдём из формулы (73):
Тогда равенство (82) с учётом (78),(81):
Введём обозначение
Тогда расход жидкости при истечении через отверстие найдётся по формуле
Выясним физический смысл коэффициента расхода m. Из равенства (82)
То есть коэффициент расхода m показывает, чему равно отношение действительного расхода через отверстие к теоретическому расходу, так как действительный расход Q всегда меньше теоретического QТЕОР, то m < 1. Значение коэффициента сжатия ε, сопротивления ζ, скорости φ и расхода μ для круглого отверстия можно определить по эмпирически построенным зависимостям. На рис.61 показаны зависимости коэффициентов ε, ζ и μ от числа Рейнольдса, подсчитанного для идеальной скорости
где ν - кинематическая вязкость.
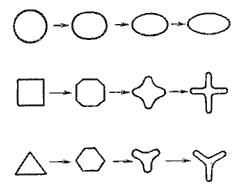
При истечении струи в атмосферу из малого отверстия в тонкой стенке происходит изменение формы струи по ее длине, называемое инверсией струи (рис.62). Обуславливается это явление в основном действием сил поверхностного натяжения на вытекающие криволинейные струйки и различными условиями сжатия по периметру отверстия. Инверсия больше всего проявляется при истечении из некруглых отверстий.
Истечение жидкости через насадки При постоянном напоре
Насадок — это короткая трубка длиной
Рис.63 Истечение через насадок внешний цилиндрический
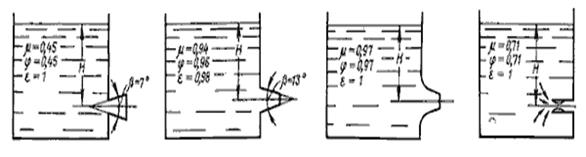
Рис. 64 а, б, в,г, –, конический расходящийся, конически сходящийся, коноидальный, внутренний цилиндрический.
Формулы для расчета скорости истечения через насадки и расхода — те же, что и при истечении через малое отверстие в тонкой стенке:
Значения коэффициентов j, e, m, z для круглого отверстия в тонкой стенке и для насадков различных типов приведены в таблице 4 Таблица 4 — Значения коэффициентов j, e, m, z для круглого отверстия в тонкой стенке и для насадков различных типов
Рассмотрим истечение жидкости, например, через внешний цилиндрический насадок (рисунок 63). Струя, попадая в насадок, встречает на своём пути отверстие и сжимается, то есть сжатое сечение находится внутри насадка, и жидкость покидает насадок полным сечением, без сжатия, потому коэффициент сжатия для насадков
тогда коэффициент расхода для насадков
коэффициенты скорости истечения и расхода для насадков одинаковы. Уравнение Бернулли для сечений 1 — 1 и 2 — 2 (потери напора не учитываем):
Если плоскость сравнения проходит по оси насадка, то z1 = z2. Тогда уравнение (81) принимает вид
Из уравнения расхода
следует, что так как S1 < S2, то u1 > u2, тогда из уравнения (84) следует, что должно выполняться неравенство то есть внутри насадка давление меньше атмосферного — внутри насадков образуется вакуум, который оказывает подсасывающее действие, поэтому расход через насадок больше, чем через отверстие того же диаметра. Например, сравним расход жидкости через внешний цилиндрический насадок и через круглое отверстие в тонкой стенке:
Сравнение производим при одинаковых условиях истечения, то есть Sнас = Sотв и Ннас = Нотв, тогда равенство (85) принимает вид:
То есть на 32 % расход через внешний цилиндрический насадок за счёт подсасывающего действия вакуума больше, чем через отверстие того же диаметра.

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
 Струя, вытекая из отверстия, сжимается. Сжатие струи происходит благодаря кривизне линий тока, крайние из которых и определяют форму струи.
Струя, вытекая из отверстия, сжимается. Сжатие струи происходит благодаря кривизне линий тока, крайние из которых и определяют форму струи. Рисунок 60 — Истечение жидкости через малое отверстие в тонкой стенке при постоянном напоре
Рисунок 60 — Истечение жидкости через малое отверстие в тонкой стенке при постоянном напоре
 (73)
(73) (74)
(74) потери напора по длине очень невелики:
потери напора по длине очень невелики: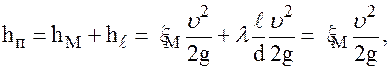
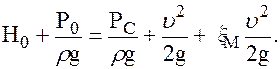 (75)
(75) (76)
(76)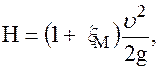
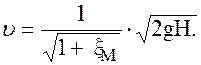
 коэффициент скорости истечения, тогда скорость в сжатом сечении струи
коэффициент скорости истечения, тогда скорость в сжатом сечении струи (77)
(77)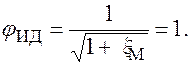
 (78)
(78) ,
, (79)
(79) (80)
(80) (81)
(81) — коэффициент расхода.
— коэффициент расхода. (82)
(82) ,
,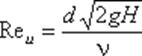

 присоединённая к отверстию того же диаметра (рисунок 63).
присоединённая к отверстию того же диаметра (рисунок 63).
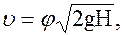
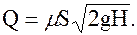
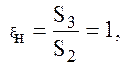
 —
— (83)
(83) (84)
(84)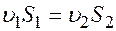
 —
— (85)
(85)