|
|
Теория механизмов и машинТема 1. Основные понятия теории механизмов и машин Теория механизмов и машин – научная дисциплина, которая изучает строение (структуру), кинематику и динамику механизмов в связи с их анализом и синтезом (И. И. Артоболевский) Цель теории механизмов и машин – анализ и синтез типовых механизмов и их систем. Анализ – исследование кинематических и динамических свойств уже существующего механизма по заданной схеме. Синтез – проектирование схемы механизма по заданным свойствам. Задачи теории механизмов и машин – разработка общих методов исследования структуры, геометрии, кинематики и динамики типовых механизмов и их систем. Типовыми механизмами называются простые механизмы, имеющие при различном функциональном назначении широкое применение в машинах, для которых разработаны типовые методы и алгоритмы синтеза и анализа. Деталь – элемент конструкции, не имеющий в своем составе внутренних связей (состоящий из одного твердого тела). Звено – твердое тело или система жестко связанных твердых тел (может состоять из одной или нескольких деталей) входящая в состав механизма.
Различают следующие виды звеньев: Входные звенья – звенья, которым сообщается заданное движение и соответствующие силовые факторы (силы или моменты); Выходные звенья – звенья, на которых получают требуемое движение и силы. Простые звенья – звенья, состоящие из одной детали; Сложные звенья – звенья, состоящие из нескольких, жестко скрепленных друг с другом и совершающих одно и тоже движение. Узел – несколько деталей, связанных между собой функционально, конструктивно или каким-либо другим образом. Связи – отношения между элементами, предназначенные для передачи материала, энергии или информации между элементами. Связи могут осуществляться с помощью различных физических средств: механических соединений, жидкостей, электромагнитных или других полей, упругих элементов. Механические соединения могут быть подвижными (кинематические пары) и неподвижными. Неподвижные соединения делятся на разъемные (винтовые, штифтовые) и неразъемные (сварные, клеевые). Механизмом называется система, состоящая из звеньев и кинематических пар, образующих замкнутые или разомкнутые цепи, которая предназначена для передачи и преобразования перемещений входных звеньев и приложенных к ним сил в требуемые перемещения и силы на выходных звеньях. Кинематическая пара – подвижное соединение двух звеньев, допускающее их определенное относительное движение. Кинематическая цепь – система звеньев, образующих между собой кинематические пары. Машины и их классификация. Машина – техническое устройство, выполняющее преобразование энергии, материалов и информации с целью облегчения физического и умственного труда человека, повышения его качества и производительности. Существуют следующие виды машин: 1. Энергетические машины– машины,преобразующие энергию одного вида в энергию другого вида. Эти машины бывают двух разновидностей: двигатели, которые преобразуют любой вид энергии в механическую (например, электродвигатели преобразуют электрическую энергию, двигатели внутреннего сгорания преобразуют энергию расширения газов при сгорании в цилиндре); генераторы, которые преобразуют механическую энергию в энергию другого вида (например, электрогенератор преобразует механическую энергию паровой или гидравлической турбины в электрическую). 2. Рабочие машины – машины, использующие механическую энергию для совершения работы по перемещению и преобразованию материалов. Эти машины тоже имеют две разновидности: - транспортные машины – машины, которые используют механическую энергию для изменения положения объекта (его координат); - технологические машины – машины,использующие механическую энергию для преобразования формы, свойств, размеров и состояния объекта. 3. Информационные машины – машины, предназначенные для обработки и преобразования информации. Они подразделяются на: - математические машины – машины, преобразующие входную информацию в математическую модель исследуемого объекта; - контрольно-управляющие машины – машины, преобразующие входную информацию (программу) в сигналы управления рабочей или энергетической машиной. 4. Кибернетические машины – машины, управляющие рабочими или энергетическими машинами, которые способны изменять программу своих действий в зависимости от состояния окружающей среды (т.е. машины, обладающие элементами искусственного интеллекта). Классификация кинематических пар. Кинематические пары классифицируются по следующим признакам: 1. По виду места контакта (места связи) поверхностей звеньев: - низшие пары – пары, в которых контакт звеньев осуществляется по плоскости или поверхности (пары скольжения); - высшие пары – пары, в которых контакт звеньев осуществляется по линиям или точкам (пары, допускающие скольжение с перекатыванием). 2. По относительному движению звеньев, образующих пару: - вращательные; - поступательные; - винтовые; - плоские; - сферические. 3. По способу замыкания (обеспечения контакта звеньев пары): - силовое (за счет действия сил веса или силы упругости пружины рис. 3.3.1, а); - геометрическое (за счет конструкции рабочих поверхностей пары рис. 3.3.1, б).
а б Рис. 3.3.1 4. По числу условий связи, накладываемых на относительное движение звеньев (число условий связи определяет класс кинематической пары). 5. По числу подвижностей в относительном движении звеньев. Число ограничений (S), накладываемых кинематической парой на движение одного звена относительно другого и зависящих от способа соединения звеньев, называется условиями связи. Если одно из звеньев кинематической пары остановить и связать с неподвижной системой координат (стойкой или корпусом), то для второго звена число степеней свободы (Н)в относительном движении (подвижность пары) будет равно Н = 6 – S. По числу степеней свободы кинематические пары подразделяются на одноподвижные (Н = 1, S = 5), двухподвижные (Н = 2, S = 4), трехподвижные (Н = 3, S = 3), четырехподвижные (Н = 4, S = 2) и пятиподвижные (Н = 5, S = 1). При S = 0 кинематические пары не существуют, так как два тела независимы друг от друга. При S = 6два тела не имеют относительного движения и превращаются в одно звено.
Рис. 3.3.2 Виды одноподвижных кинематических пар: - - вращательная (рис. 3.3.2, б) – кинематическая пара с геометрическим замыканием по цилиндрической поверхности, допускает вращательное движение одного звена относительно другого звена; - винтовая (рис. 3.3.2, в) – кинематическая пара, в которой поступательное движение вдоль оси связано определенной зависимостью с вращательным движением вокруг оси.
Виды двухподвижных кинематических пар: - цилиндрическая (рис. 3.3.2, г) – кинематическая пара, с геометрическим замыканием, допускает независимые вращательное и поступательное относительные движения звеньев; - сферическая (рис. 3.3.2, д) кинмаетическая пара с пальцем, который перемещается в кольцевом пазу, допускает поворот вокруг оси пальца и поворот относительно оси, перпендикулярной плоскости кольцевого паза и проходящей через центр сферы. Виды трехподвижных кинематических пар: - сферическая (шаровой шарнир) (рис. 3.3.2, е) – кинематическая пара с геометрическим замыканием, допускает три независимых относительных вращения звеньев вокруг осей х, у, z; - плоскостная (рис. 3.3.2, ж) – кинематическая пара с силовым замыканием силой тяжести звена, допускает два поступательных движения вдоль осей х и у и вращательное вокруг оси z. Четырехподвижная кинематическая пара: цилиндр-плоскость (рис. 3.3.2, з) – кинематическая пара,в которой происходит движение цилиндра относительно плоскости или вращение вокруг осей х и y и скольжение вдоль осей х и у. Пятиподвижная кинематическая пара: шар–плоскость (рис. 3.3.2, и) – кинематическая пара, в которой происходит, движение шара относительно плоскости, три вращения вокруг осей х, у, z и скольжение по плоскости вдоль осей х и у. Поступательное движение шара вдоль оси z вниз невозможно, так как ограничено плоскостью, а при движении вверх происходит отрыв шара от плоскости, и кинематическая пара перестает существовать. Требует силового замыкания. Тема 2. Структурный анализ и синтез механизмов Структурный анализ – это исследование имеющегося механизма для определения его состава путем расчленения на структурные группы и начальный механизм в порядке, обратном образованию механизма. Как на любом этапе проектирования, при структурном синтезе различают задачи синтеза и задачи анализа. Задачей структурного анализа является определения параметров структуры заданного механизма – числа звеньев и структурных групп, числа и вида КП, числа подвижностей (основных и местных), числа контуров и числа избыточных связей. Задачей структурного синтеза является синтез структуры нового механизма, обладающего заданными свойствами: числом подвижностей, отсутствием местных подвижностей и избыточных связей, минимумом числа звеньев, с парами определенного вида (например, только вращательными, как наиболее технологичными) и т.п. При выполнении структурного анализа на структурной схеме среди звеньев, наиболее удаленных от входного звена, отыскивается группа Ассура, которую можно отсоединить без нарушения строения оставшихся звеньев механизма. Эту группу изображают отдельно. Среди оставшихся звеньев отыскивают следующую удаленную от входного звена группу Ассура, также изображая ее отдельно. Таким образом, находят все группы Ассура, пока не останется одно входное звено – начальный механизм. Структурная схема механизма – графическое изображение механизма, выполненное с использованием условных обозначений, рекомендованных ГОСТом или принятых в специальной литературе, содержащее информацию о числе и расположении элементов (звеньев, групп), а также о виде и классе кинематических пар (КП), соединяющих эти элементы. Основные понятия структурного синтеза и анализа. Структурная формула кинематической цепи связывает число степеней свободы (т.е. число независимых движений) с числом и видом кинематических пар в данной кинематической цепи. Основные структурные формулы были составлены для плоских механизмов П.Л. Чебышевым (1879-1962) и М. Грюблером (1851-1935), для пространственных – И.И. Сомовым (1815-1876) и А.П. Малышевым (1879-1962). Так как принципы, заложенные в построение всех этих формул одинаковы, то их можно записать в обобщенном виде: где H – число степеней подвижности твердого тела (соответственно при рассмотрении механизма в пространстве H = 6, на плоскости H = 3); n – число подвижных звеньев в механизме; n = k – 1; k – общее число звеньев механизма (включая и неподвижное звено – стойку); i – число подвижностей в КП (от 5 до 1); pi – число кинематических пар с i подвижностями. В плоском механизме все звенья движутся в одной плоскости, все оси параллельны друг другу и перпендикулярны плоскости механизма. Формула Чебышева: W = 3n – 2pн – pв, где рн – число низших КП (5-го класса);
В качестве примера вычислим степень подвижности кривошипно-ползунного механизма, изображенного на рис. 3.3.3. Здесь n =3, pн = 4, pв = 0, W = 3×3 – 2×2 = 1. Для расчета избыточных связей, согласно второму определению, используется следующая зависимость: q = W0 + Wм – W, где q – число избыточных связей в механизме; W0 – заданная или требуемая подвижность механизма; Wм – число местных подвижностей в механизме; W – расчетная подвижность механизма. Структурная классификация механизмов по Л.В. Ассуру. Для решения задач синтеза и анализа сложных рычажных механизмов профессором Петербургского университета Л.В. Ассуром (1978-1920) была предложена оригинальная структурная классификация. По этой классификации механизмы, не имеющие избыточных связей и местных подвижностей, состоят из первичных механизмов и структурных групп (рис. 3.3.4).
Рис. 3.3.4
Структурной группой Ассура (или группой нулевой подвижности) называется незамкнутая кинематическая цепь, образованная только подвижными звеньями механизма, подвижность которой при присоединении ее внешних пар к стойке равна нулю (Wгр = 0). Конечные звенья групп Ассура, входящие в две кинематические пары, из которых одна имеет свободный элемент звена, предназначенного для присоединения группы к звеньям механизма, называются поводками. Группы могут быть различной степени сложности. Структурные группы Ассура делятся на классы, числа поводков в группе, числа замкнутых контуров внутри группы. В пределах класса (по Ассуру) группы подразделяются по числу поводков на порядки (порядок группы равен числу ее поводков). Механизмы классифицируются по степени сложности групп входящих в их состав. Класс и порядок механизма определяется классом и порядком наиболее сложной из входящих в него групп. Особенность структурных групп Ассура – их статическая определимость. Если группу Ассура свободными элементами звеньев присоединить к стойке, то образуется статически определимая ферма. Используя группы Ассура, удобно проводить структурный, кинематический и силовой анализы механизмов. Наиболее широко применяются простые рычажные механизмы, состоящие из групп Ассура 2-го класса 2-го порядка (рис. 3.3.6). Число разновидностей таких групп для плоских механизмов с низшими парами невелико, их всего пять. 1. Группа 1-го вида – все пары вращательные. 2. Группа 2-го вида – на конце одного из звеньев поступательная пара. 3. Группа 3-го вида – в середине поступательная пара. 4. Группа 4-го вида – на конце обоих звеньев поступательные пары. 5. Группа 5-го вида – в середине и на конце одного из звеньев поступательная пара.
Рис. 3.3.6 Пример.Выполните структурный анализ механизма шарнирного четырехзвенника (четырехшарнирный механизм) (рис. 3.3.7).
Рис. 3.3.7 1. Определим степень подвижности механизма: W = 3n – 2pн – pв = 3·3 – 2·4 – 0 = 1. 2. Выделим группы Ассура (последние два звена и три кинематические пары) – группа II класса 1-го вида (II1): W = 3n –2pн – pв = 3·2 – 2·3 = 0. 3. Остается механизм I класса: W = 3·1 – 2·1 = 1. Данный механизм образован присоединением к механизму I класса группы Ассура II класса 1-го вида, т. е. весь механизм является механизмом II класса. Структура механизма записывается в следующей форме: I ® II1. Основные виды плоских рычажных механизмов. Простейшие четырехзвенные плоские механизмы состоят из одного неподвижного звена (стойки) и трех подвижных звеньев (рис. 3.3.8, а – д).
Рис. 3.3.8. Рычажные механизмы: а – кривошипно-ползунный механизм; б – четырехшарнирный механизм; в – четырехзвенный кулисный механизм; г – синусный механизм; д – тангенсный механизм; е – шестизвенный кулисный механизм: 1 – кривошип, 2 – шатун, 3 – коромысло Если все пары вращательные, то механизм называется шарнирным четырехзвенником. Кривошип – звено, которое совершает полный оборот вокруг оси вращения. Коромысло – звено, которое совершает вращательное движение на неполный оборот. Шатун – звено, совершающее плоскопараллельное движение. Если звено 3 соединить со стойкой поступательной парой, то оно будет называться ползуном, а весь механизм – кривошипно-ползунным (рис. 3.3.8, а). Ползун – звено, которое совершает возвратно-поступательное движение. В том случае, если поступательная пара находится между звеньями 2 и 3, т. е. звено 2 перемещается по подвижной направляющей, механизм называется кулисным (рис. 3.3.8). Если коромысло служит подвижной направляющей для ползуна, то его называют кулисой, а ползун – кулисным камнем. Более сложные плоские кулисные механизмы образуются присоединением структурных групп различных видов, которые были рассмотрены выше (рис. 3.3.8, е). Тема 3. Кинематический анализ механизмов Кинематический анализ.Кинематическое исследование механизма состоит в изучении движения звеньев без учета сил, действующих на эти звенья, при заданном движении ведущего звена. Кинематический анализ выполняется по кинематической схеме механизма. Он состоит в определении кинематических характеристик: - перемещений звеньев и траекторий, описываемых характерными точками звеньев; - линейных скоростей и ускорений точек звеньев механизма; - угловых скоростей и угловых ускорений звеньев механизма. Кинематический анализ позволяет установить соответствие кинематических параметров (перемещений, скоростей и ускорений) заданному закону движения механизма, а также получить исходные данные для выполнения динамического анализа. По полученным кинематическим характеристикам определяют инерционные нагрузки звеньев, кинетическую энергию механизма, закон движения ведущего и ведомых звеньев в функции времени. Кинематическое исследование механизмов проводят графическими и аналитическими методами. Графическое определение кинематических параметров основано на геометрических построениях, погрешность результатов которых составляет 0,3–0,5 % по сравнению с аналитическими расчетами. Графический метод нагляден и универсален, так как позволяет определять положения, скорости и ускорения звеньев механизма любой структуры. Метод построения планов скоростей и ускорений применяется при инженерных расчетах как при анализе, так и при синтезе механизмов. Графический метод построения кинематических диаграмм позволяет использовать при анализе заданные в виде графиков законы изменения кинематических параметров в функции обобщенных координат j и t. Точность графических методов достаточна для выполнения технических расчетов. Графические методы не могут быть использованы, если требуется проводить расчеты с высокой точностью. Применение ЭВМ при аналитическом исследовании упрощает выполнение сложных и трудоемких вычислений. При кинематическом исследовании различают абсолютное и относительное движения звеньев и кинематических пар механизма и соответствующие им кинематические характеристики. Абсолютное движение – движение точки или тела относительно неподвижной системы координат, связанной с не подвижными стойкой или корпусом. Относительное движение– движение точки или звена относительно подвижной системы координат, которая связана с каким-либо движущимся звеном. Движение подвижной системы координат относительно неподвижной системы координат называется переносным движением. Перемещение (как скалярная величина) – мера пути, пройденного точкой или звеном за некоторое время: линейное перемещение (S) измеряется в метрах, угловое (j) – в градусах или радианах. Угол в 1 рад соответствует центральному углу окружности, длина дуги которой равна ее радиусу. В окружности 2p таких отрезков, поэтому 1 рад = 360/(2p) = 57,3°. Скорость – основная кинематическая характеристика (векторная величина) – мера быстроты движения, характеризующая перемещение точки в рассматриваемый момент времени (в рассматриваемом положении) в данной системе отсчета. Линейная скорость (V) измеряется в м/с, угловая (w) – в с–1. Ускорение (векторная величина) – мера быстроты изменения скорости в данный момент в данной системе отсчета. Размерность линейного ускорения а (м/с2), углового e (с–2). Из теоретической механики известна теорема сложения скоростей: Вектор абсолютной скорости Это уравнение для точки В звена (рис. 3.3.9, а) имеет вид
Рис. 3.3.9 Вектор скорости Вектор линейной скорости точки звена во вращательном движении Вектор абсолютного ускорения
где Нормальное ускорение направлено по радиусу вращения точки к центру кривизны траектории (вдоль звена от точки В к точке А), а касательное ускорение направлено перпендикулярно звену АВ в сторону углового ускорения е звена (см. рис. 3.3.9, б). Направление угловой скорости w и углового ускорения e совпадают при равноускоренном движении звена и противоположны друг другу при равнозамедленном движении. При поступательном движении звена векторы абсолютных скоростей и абсолютных ускорений всех точек звена равны и направлены по касательной к траектории движения. Направление векторов скоростей совпадает с направлением движения, а для ускорений при ускоренном движении эти векторы направлены в сторону движения, при замедленном – в обратную сторону (рис. 3.3.9, в). Планы положений механизма. Планом положений механизма называется графическое изображение кинематической схемы в выбранном масштабе, соответствующее заданному положению начального звена. Планы строятся в заданном масштабе. При этом различают понятия «масштаб» и «масштабный коэффициент».Масштабом физической величины называют длину отрезка в миллиметрах, изображающую единицу измерения этой величины. Масштабным коэффициентом физической величины называют отношение численного значения физической величины к длине отрезка в миллиметрах, изображающего эту величину. Масштаб и масштабный коэффициент являются взаимно обратными величинами. Масштабные коэффициенты обозначают буквой m с индексом, указывающим, к какой величине они относятся. Например, масштабный коэффициент длин (ml) для плана механизма есть отношение какой-либо длины (lAB) в метрах к отрезку (АВ), изображающему эту длину на чертеже в миллиметрах:
Рассмотрим построение планов механизма на примерах. 1. Шарнирный четырехзвенник (рис. 3.3.10). Кривошип ОА вращается с постоянной скоростью w, поэтому положение точки А известно для любого момента времени (любого угла поворота звена ОА).
Рис. 3.3.10 Делим окружность радиуса ОА на несколько равных частей, например, на 6. Обозначим положения конца кривошипа точками А1, А2, …, А6. Точка В (конец коромысла) движется по дуге окружности радиуса СВ. Проведем эту дугу из центра – точки С. Радиусом, равным длине шатуна АВ, делаем из точек А1, A2, ... A6 засечки на дуге окружности. Соединяем одноименные положения точек А1 и В1, А2 и В2, а также В1 и С1, В2 и С2. Получаем положения шатуна и коромысла за цикл движения, т. е. за один оборот кривошипа. Вращение коромысла против часовой стрелки соответствует положениям рабочего хода, по часовой стрелке – положениям холостого хода. 2. Кривошипно-ползунный механизм (рис. 3.3.11). Задаемся крайним положением кривошипа (кривошип и шатун располагаются на одной линии).
Рис. 3.3.11 Делим окружность радиуса ОА на равные части. Из точек деления (А1, А2, ...) делаем засечки на оси движения ползуна (В1, В2, ...) радиусом, равным длине шатуна. Найденные положения точки В определяют положение поршня (ползуна) на рабочем ходу – В1, В2, В3; на холостом ходу – В4, В5. Соединяем одноименные точки (А1 и B1, A2 и В2 и т.д.). Планы скоростей плоских механизмов. Планом скоростей называют чертеж, на котором изображены в виде отрезков векторы, равные по модулю и по направлению скоростям различных точек механизма в данном положении. Для построения плана скоростей необходимы исходные данные: - план механизма с указанием размеров; - угловая скорость начального звена. Из теоретической механики известно, что любое движение плоского тела может рассматриваться как сумма двух движений: вращение относительно некоторой точки (полюса) и поступательное (переносное) движение полюса. Используя этот принцип, рассмотрим решение задач о скоростях точек звеньев, образующих пары 5-го класса. Пример.Определение скоростей точек звена, входящего во вращательную пару с другим звеном (рис. 3.3.12).
Требуется определить:скорости точек В и С (VB, VС ). В соответствии с теоремой сложения скоростей, абсолютная скорость (VB) точки равна геометрической сумме переносной (VA) и относительной (VВА) скоростей этой точки:
где VBA = wAB lAB – относительная скорость точки В во вращательном движении вокруг точки А; вектор VBA направлен перпендикулярно звену АВ (т. е. радиусу вращения). 2. Аналогично
где VCA = wAB lAC; вектор этой скорости направлен перпендикулярно звену АС (VCA ^ AC). 3. Построим векторные уравнения (3.3.1) и (3.3.2). Выбираем произвольную точку р – полюс плана скоростей и откладываем в направлении вектора VA отрезок произвольной длины ра (см. рис. 3.3.12, б). При этом определяем значение масштабного коэффициента плана скоростей: mу = VА/ра. (3.3.3) Строим вектор
Суммарный вектор – абсолютная скорость точки В – определится отрезком рb:
Аналогично находим скорость точки с: из точки а в направлении, перпендикулярном ас, откладываем относительную скорость с учетом масштабного коэффициента: ac = wABlAC /mV. (3.3.6) Соединяем полюс с полученной на плане скоростей точкой с. Измерив на плане величину отрезка рс, находим значение абсолютной скорости точки с:
Скорость точки С можно определить, приняв движение точки в за переносное:
На плане скоростей вектор pb изображает скорость точки в; относительная скорость Vcb – это вектор bc , направленный перпендикулярно стороне звена ВС (см. рис. 3.3.12, а). Соединив точки b и с, получим на плане скоростей графическое изображение уравнения (3.3.8). Сравнивая треугольники ABC и аbс на рис. 3.3.12, можно заметить, что эти фигуры подобны и сходственны, т. к. стороны их взаимно перпендикулярны и отрезки ab, ас, bс пропорциональны длинам сторон звена АВ, АС, ВС. Выводы: 1. На плане скоростей лучи, выходящие из полюса, изображают абсолютные скорости точек звена, а отрезки, соединяющие концы лучей, – относительные скорости соответствующих точек. 2. Векторы относительных скоростей направлены на плане скоростей к первой букве индекса. Например, VCB – скорость точки С относительно В. На плане скоростей читается наоборот: отрезок bc , а вектор направлен к точке с. 3. Векторы относительных скоростей точек жесткого звена образуют на плане скоростей фигуру, подобную этому звену, повернутую на 90° в направлении угловой скорости звена. Последний вывод называется принципом подобия в плане скоростей и позволяет определить скорость любой точки звена графически, если известны скорости хотя бы двух точек этого звена. Планы ускорений плоских механизмов.Чертеж, на котором изображены в виде отрезков векторы, равные по модулю и направлению ускорениям различных точек звеньев механизма в данном положении, называется планом ускорений. Рассмотрим решение двух задач об определении ускорений точек звеньев, образующих кинематические пары 5-го класса, аналогично решению задач о скоростях. Пример.Определите ускорение точек звена, входящего во вращательную пару (рис. 3.3.13).
Решение. 1. Абсолютное ускорение точки В складывается из переносного ускорения (
2. Поскольку относительное движение вращательное, выражение (3.3.9) можно записать в виде
где
3. Построим уравнение (3.3.10) в виде суммы векторов (см. рис. 3.3.13, б). Выбираем точку p – плюс плана ускорений. Откладываем из полюса вектор mа = аА/pа. (3.3.11) Из точки а откладываем в направлении к центру вращения с учетом масштаба вектор нормального ускорения (an÷ïBA). Величина отрезка an определяется соотношением
От полученной точки n в направлении, перпендикулярном АВ, откладываем отрезок nb, изображающий в масштабе касательную, составляющую относительного ускорения:
Направление вектора nb определяется с учетом направления углового ускорения Соединяя точку п с точкой b, получаем результирующий вектор, который изображает абсолютное ускорение точки В (см. уравнение (3.3.10)):
Аналогично строятся векторные уравнения для точки С (см. рис. 3.3.13):
4. Определим значения полных относительных ускорений:
5. С учетом известных из теоретической механики формул (см. значения величин, входящих в уравнение (3.3.10))
Аналогично
6. Определим тангенс угла, определяющего направление полного относительного ускорения (см. рис. 3.3.12, а):
Из формулы (3.3.21) следует, что tgj не зависит от того, какая точка звена рассматривается, и одинаков для всех относительных ускорений. Из выражений (3.3.18) – (3.3.21) следует, что относительные ускорения точек звена ABC пропорциональны длинам сторон и повернуты на один и тот же угол. Следовательно, Dabc в плане ускорений и DАВС (жесткое звено) подобны и сходственны. Этим определяется принцип подобия в плане ускорений. Векторы относительных ускорений точек жесткого звена образуют на плане ускорений фигуру, подобную этому звену и повернутую относительно его на угол (180° – j) в направлении углового ускорения. Зная относительные ускорения хотя бы двух точек звена, можно определить ускорение любой точки этого звена, пользуясь принципом подобия. Тема 4. Силовой анализ и расчет механизмов Задачи и методы силового анализа. Силовой анализ– это изучение влияния внешних сил на звенья механизма, на кинематические пары и на неподвижные опоры. Исследование действия сил необходимо для того, чтобы можно было рассчитать звенья на прочность, износостойкость, виброустойчивость, чтобы определить необходимую мощность привода. В результате силового анализа можно определить пути уменьшения динамических нагрузок и спроектировать машину так, чтобы она имела достаточную прочность при меньших габаритах и массе. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|
поступательная кинаметическая пара (рис. 3.3.2, а) – кинематическая пара, с геометрическим замыканием, допускает лишь прямолинейное возвратно-поступательное относительное движение;
.
рв – число высших КП (4-го класса).
Под первичным механизмомпонимают механизм, состоящий из двух звеньев (одно из которых неподвижное), образующих кинематическую пару с одной Wпм = 1 или несколькими Wпм > 1 подвижностями. Примеры первичных механизмов даны на рис. 3.3.5.
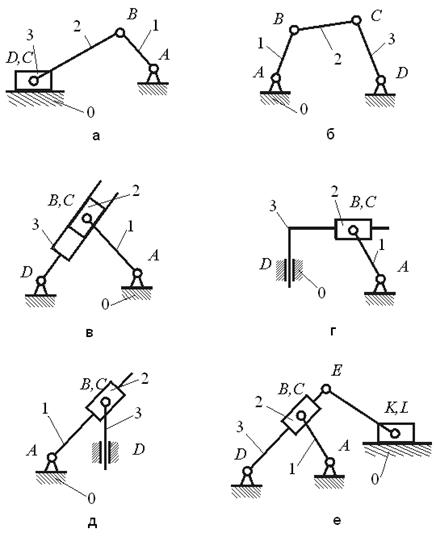
точки В звена равен геометрической сумме вектора скорости 
произвольно выбранной точки А звена и вектора скорости 
во вращательном движении относительно этой точки.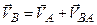
.
известен по величине и направлению.
направлен в сторону движения звена (по угловой скорости со звена) по касательной к траектории, т.е. перпендикулярно звену ВА ( 
BА).
точки В звена равен геометрической сумме вектора ускорения 
произвольно выбранной точки А и вектора ускорения 
во вращательном движении относительно этой точки (рис. 3.3.9, б).
,
– соответственно относительное нормальное (центростремительное) и касательное (тангенциальное) ускорения во вращательном движении.
.
Пусть заданы: 
– вектор скорости точки А (см. рис. 3.3.12, а); wАВ – угловая скорость звена АВ.
, (3.3.2)
. Из точки а проводим прямую, перпендикулярную аb, и откладываем отрезок аb в масштабе, учитывая при этом направление угловой скорости wАВ:
. (3.3.4)
. (3.3.5)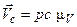
(3.3.7)
(3.3.8)
При построении плана ускорений считается, что все скорости известны, т. е. план скоростей механизма для данного положения уже построен.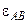
– угловое ускорение звена ABC.
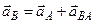. (3.3.9)
, (3.3.10)
– нормальное ускорение в относительном движении, направленное по радиусу вращения (АВ) к центру вращения (точке А);
– касательное ускорение в относительном движении, направленное перпендикулярно радиусу вращения.
. (3.3.12)
. (3.3.13)
(в данном примере – вниз).
. (3.3.14)
; (3.3.15)
. (3.3.16)
. (3.3.17)
. (3.3.18)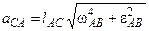
; (3.3.19)
. (3.3.20)
. (3.3.21)