
|
|
Расчеты на устойчивость. Порядок выполнения расчета на устойчивость.1. Получение сведений о материале стержня для определения предельной гибкости стержня расчетным путем или по таблице:
2. Получение сведений о геометрических размерах поперечного сечения, длине и способах закрепления концов для определения категории стержня в зависимости от гибкости:
где А – площадь сечения; Jmin – минимальный момент инерции (из осевых);
где m – коэффициент приведенной длины. 3. Выбор расчетных формул для определения критической силы и критического напряжения: - при l < lпред расчет ведется по эмпирическим формулам; - при l > lпред расчет ведется по формуле Эйлера. 4. Проверка и обеспечение устойчивости. При расчете по формуле Эйлера условие устойчивости определяется по формуле
где F – действующая сжимающая сила; [ny]– допускаемый коэффициент запаса устойчивости. При расчете по формуле Ясинского sкр = а – bl, где а, b – расчетные коэффициенты, зависящие от материала;
В случае невыполнения условий устойчивости необходимо увеличить площадь поперечного сечения. Иногда необходимо определить запас устойчивости при заданном погружении:
При проверке устойчивости сравнивают расчетный запас выносливости с допускаемым: ny £ [ny]. Тема 9. Динамические нагрузки Как уже известно, статическойназывается нагрузка, которая весьма медленно возрастает от нуля до своего конечного значения. Ускорения частиц элементов конструкции от такой нагрузки невелики, а потому можно пренебречь возникающими при этом силами инерции. При быстро возрастающей нагрузке необходимо учитывать силы инерции, появляющиеся в результате деформации системы; силы инерции необходимо учитывать также при действии нагрузки, вызывающей движение тела с некоторым ускорением. Нагрузки, учитывающие силы инерции, а также вызванные этими нагрузками напряжения и деформации называются динамическими. Все динамические нагрузки делятся на инерционные, ударные и повторно-переменные (цикловые). К динамическим также относятся ударные нагрузки, хотя при расчете на удар в ряде случаев пренебрегают силами инерции, возникающими в конструкции. Удар – это взаимодействие тел, при котором за очень малый промежуток времени скачкообразно возникают конечные изменения скорости этих тел. Расчет на действие динамической нагрузки (динамический расчет) производят при проектировании частей конструкций, находящихся под действием ударной или вибрационной нагрузки, создаваемой станками, двигателями, молотами и другими механизмами и вызывающей колебания сооружений. Многие части машин также находятся под действием динамической нагрузки. Динамический расчет имеет целью обеспечить необходимую прочность конструкции и не допустить значительных ее деформаций. При динамической нагрузке любой элемент конструкции в каждый момент времени можно рассматривать как находящийся в состоянии равновесия под действием внешних сил (включая опорные реакции), усилий, представляющих собой действие соседних элементов, и сил инерции. Это положение носит название принципа Даламбера. Таким образом, при инерционных нагрузках расчет ведется с применением принципа Даламбера. При ударных нагрузках расчет ведется по коэффициенту динамичности, а при повторно-переменных нагрузках – по пределу выносливости материала. Расчет на прочность с учетом сил инерции. N = Р + mа, где Р1 – движущая сила, Н; Р – сила сопротивления, Н; mа – сила инерции.
где А – площадь поперечного сечения. Расчет на прочность при ударе (рис. 3.2.44). Все расчеты на динамические нагрузки основаны на расчетах при статических нагрузках путем применения коэффициента динамичности:
Условие прочности: sд max = kдsст £ [s].
Если ударяемая конструкция не имеет в точке удара сосредоточенной массы, то
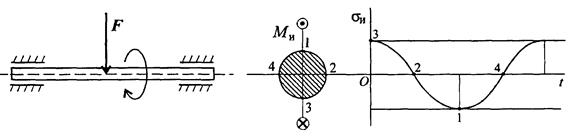
На практике обычно принимают Тема 10. Усталость Основные понятия. Многие детали машин работают в условиях переменных во времени напряжений. Так, вращающиеся валы и оси, нагруженные постоянными изгибающими силами, работают при переменных нормальных напряжениях изгиба. Совокупность последовательных значений переменных напряжений за один период процесса их изменения называется циклом. Обычно цикл представляют в виде графика, в котором по оси абсцисс откладывается время, а по оси ординат – напряжения (рис. 3.2.45).
Рис. 3.2.45 Цикл характеризуется максимальным, минимальным исредним напряжениями. Среднее значение напряжений (sm), амплитуда цикла (sа)и коэффициент асимметрии цикла (R) рассчитываются по формулам: Все приведенные определения и соотношения можно записать и для касательных напряжений.
sт = 0; sa = sт; R = – 1.
Переменные напряжения возникают в осях вагонов, рельсах, рессорах, валах машин, зубьях колес и многих других случаях. Под действием переменных напряжений в материале возникает микротрещина, которая под действием повторяющихся напряжений растет в глубь изделия. Края трещины трутся друг о друга, и трещина быстро увеличивается. Поперечное сечение детали уменьшается, и в определенный момент случайный толчок, или удар вызывает разрушение. Появление трещин под действием переменных напряжений называют усталостным разрушением. Усталостью называют процесс накопления повреждений в материале под действием повторно-переменных напряжений. Характерный вид усталостных разрушений – трещины и часть поверхности, блестящая в изломе. Такой характер излома вызван многократным нажатием, зашлифованностью частей детали. Опыт показывает, что усталостное разрушение происходит при напряжениях ниже предела прочности, а часто и ниже предела текучести. Способность материала противостоять усталостным разрушениям зависит от времени действия нагрузки и от цикла напряжений. При любой деформации нагружение с симметричным циклом наиболее опасно. Опытным путем установлено, что существует максимальное напряжение, при котором материал выдерживает, не разрушаясь,значительное число циклов. Наибольшее (максимальное) напряжение цикла, при котором не происходит усталостного разрушения образца из данного материала после любого большого числа циклов, называют пределом выносливости. Для определения предела выносливостиизготавливают серию одинаковых образцов и проводят испытания при симметричном цикле изгиба. Образцы имеют цилиндрическую форму, гладкую поверхность (полированную) и плавные переходы. Образцы устанавливают на испытательную машину и нагружают так, чтобы напряжение составляло примерно 80 % от предела прочности. После некоторого числа циклов образец разрушается. Фиксируют максимальное напряжение и число циклов до разрушения. Испытания повторяют, постепенно снижая нагрузку на каждый последующий образец и фиксируя число циклов до разрушения образцов. По результатам испытаний строят график зависимости между максимальным напряжением и числом циклов нагружений до разрушения.График называют кривой усталости (рис. 3.2.48). В большинстве случаев после числа циклов нагружений более 107 кривая приближается к прямой, параллельной оси абсцисс.
Рис. 3.2.48 n – число циклов нагружения; sR – предел выносливости; s–1 – предел выносливости при симметричном цикле (R = – 1); s0 – предел выносливости при отнулевом цикле (R = 0); nбаз – число циклов, при котором определяют предел выносливости (базовое число циклов) Если провести испытания при асимметричном цикле, кривая ляжет выше, т. е. выносливость материала повысится. Предел выносливости, определенный путем стандартных испытаний, является одной из механическиххарактеристик материала. Факторы, влияющие на сопротивление усталости: 1. Концентрация напряжений. В местах, где имеются резкие изменения размеров, отверстия, резьба, острые углы, возникают большие местные напряжения (концентрация напряжений). В этих местах возникают усталостные трещины, трещины разрастаются, и это приводит к разрушению детали. Местные напряжения значительно выше номинальных напряжений, возникающих в гладких деталях. Влияние концентрации напряжений учитывается эффективным коэффициентом концентрации напряжений (Кs). Коэффициент зависит от формы поверхности. 2. Размеры детали. В деталях больших размеров возможны внутренняя неоднородность, инородные включения, незаметные микротрещины. Влияние размеров учитывается масштабным фактором (Kd-). Kd – масштабный коэффициент, коэффициент влияния абсолютных размеров. 3. Характер обработки поверхности. Поверхность может быть шероховатой, покрытой следами от резца, т.е. ослабленной, а может быть усиленной специальными методами упрочнения: азотированием, поверхностной закалкой, цементацией. При отсутствии специального упрочнения поверхностный коэффициент меняется от 0,6 до 1. При специальной обработке он может быть больше единицы: поверхность оказывается прочнее сердцевины. КF – коэффициент влияния шероховатости; Ку – коэффициент влияния упрочнения, Ку = 1,1 – 2,8. Одновременный учет действия всех факторов, понижающих предел выносливости, можно провести с помощью коэффициента
Находим предел выносливости в расчетном сечении:
Основы расчета на прочность при переменных напряжениях. Расчеты по нормальным и касательным напряжениям проводятся аналогично. Расчетные коэффициенты выбираются по специальным таблицам. При расчетах определяют запасы прочности по нормальным и касательным напряжениям. Запас прочности по нормальным напряжениям находится по формуле
Запас прочности по касательным напряжениям определяется по формуле
где sа – амплитуда цикла нормальных напряжений; tа – амплитуда цикла касательных напряжений. Полученные запасы прочности сравнивают с допускаемыми. Представленный расчет является проверочным и проводится при конструировании детали. Контрольные вопросы 1. Основные понятия, гипотезы и допущения 2. Внешние силы. Определение внутренних сил методом сечений. 3. Напряжения. Основные понятия. Нормальные и касательные. 4. Растяжение и сжатие. Основные понятия. Внутренние силы и напряжения. 5. Деформации при растяжении и сжатии. 6. Расчеты на прочность. Три задачи, решаемые с помощью условия прочности. 7. Закон Гука, упругость, пластичность, хрупкость. 8. Механические характеристики материалов при растяжении (сжатии). 9. Построение эпюр напряжений, удлинений при растяжении (сжатии). 10. Сдвиг (срез). Нагрузки, напряжения, закон Гука. 11. Пример расчета заклепочных соединений. 12. Кручение. Построение эпюр крутящих моментов. 13. Кручение. Определение напряжений в любой точке поперечного сечения. Полярные моменты инерции и сопротивления вала. 14. Кручение. Закон Гука. Расчет на прочность 15. Кручение. Расчет на жесткость. 16. Построение эпюр напряжений и углов закручивания. 17. Изгиб. Типы опор балок и определение опорных реакций. Внутренние усилия. Построение эпюр изгибающих моментов. 18. Изгиб. Напряжения, деформации. 19. Изгиб. Условие прочности. Три задачи, решаемые с помощью условия прочности. 20. Сложные случаи напряжения. Внецентренное растяжение (сжатие). Косой изгиб. 21. Совместное действие изгиба с кручением. 22. Продольный изгиб. Основные понятия. 23. Метод Эйлера для определения критических сил. 24. Пределы применимости формулы Эйлера. Формула Ясинского. 25. Три типа задач, решаемые из условия прочности. 26. Расчет на устойчивость сжатых стержней. 27. Динамическое действие нагрузок. 28. Явление усталости, предел выносливости. 29. Теории прочности, используемые при расчете валов на совместное действие изгиба с кручением. 30. Пути повышения усталостной прочности. Конструктивные и технологические мероприятия. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
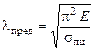 .
.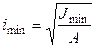 ,
,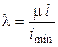 ,
,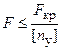 ;
; 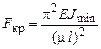 ,
,
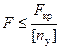 .
.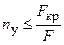 .
. Пусть стержень движется прямолинейно и параллельно своей оси (рис. 3.2.43). Применим принцип Даламбера, т.е. прикладываем к стержню силу инерции mа, после этого считаем, что стержень находится в состоянии статического равновесия. Находим продольную силу:
Пусть стержень движется прямолинейно и параллельно своей оси (рис. 3.2.43). Применим принцип Даламбера, т.е. прикладываем к стержню силу инерции mа, после этого считаем, что стержень находится в состоянии статического равновесия. Находим продольную силу: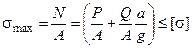 ,
,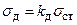 ,
, 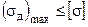 ,
,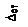
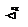
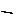
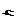
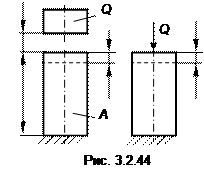 где
где 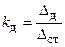 – динамический коэффициент;
– динамический коэффициент;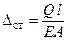 – перемещение под действием силы Q.
– перемещение под действием силы Q.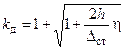 – динамический коэффициент при вертикальном ударе.
– динамический коэффициент при вертикальном ударе.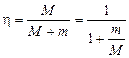 – коэффициент, учитывающий соотношение ударяемой (m) и ударяющей (М) массы.
– коэффициент, учитывающий соотношение ударяемой (m) и ударяющей (М) массы.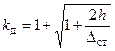 .
. .
.
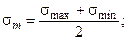
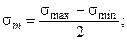
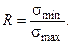
 Цикл, при котором максимальное и минимальное напряжения равны по величине и обратны по знаку, называют симметричным циклом (рис. 3.2.46).
Цикл, при котором максимальное и минимальное напряжения равны по величине и обратны по знаку, называют симметричным циклом (рис. 3.2.46).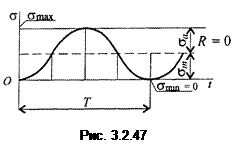 Остальные циклы называют асимметричными. Часто встречается отнулевой, или пульсирующий, цикл, минимальное напряжение при этом цикле равно нулю, среднее напряжение равно амплитуде (рис. 3.2.47).
Остальные циклы называют асимметричными. Часто встречается отнулевой, или пульсирующий, цикл, минимальное напряжение при этом цикле равно нулю, среднее напряжение равно амплитуде (рис. 3.2.47).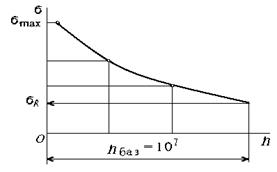
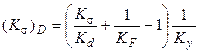 .
.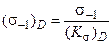 .
.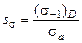 .
.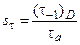 ,
,