
|
|
Угол между двумя плоскостями
Если коэффициенты
не пропорциональны, то плоскости P1 и P2 пересекаются по некоторой прямой L. Проведем плоскость P, перпендикулярную к линии L. Эта плоскость пересекается с P1 и P2 по прямым Поскольку
и определяет косинус искомого угла между плоскостями P1 и P2.
Расстояние от точки до плоскости
Пусть задана точка
Вывод этой формулы такой же, как вывод формулы расстояния от точки до прямой.
Пример 5.3. Установить взаимное расположение заданных плоскостей. Если плоскости параллельные, то найти расстояние между плоскостями; если плоскости пересекаются, найти угол между плоскостями:
Решение. 1) Определяем координаты нормальных векторов данных плоскостей: Например, в плоскости P2 выберем точку M, принадлежащую этой плоскости. Для этого, например, придадим переменным x и y значения равные нулю, т.е.
2) Определяем координаты нормальных векторов данных плоскостей: Используя формулу (5.8) находим косинус угла между этими плоскостями:
Тогда ,
6. УРАВНЕНИЕ ПРЯМОЙ В ПРОСТРАНСТВЕ
Канонические и параметрические уравнения прямой
Прямая L в пространстве определяется однозначно, если: а) известны точка, через которую она проходит, и ненулевой вектор, параллельный прямой; б) или известны две точки этой прямой.
Постановка задачи: Составить уравнение прямой, проходящей через точку
Равенства (6.1) называются каноническими уравнениями прямой в пространстве. Пусть
Так как векторы
Соотношение (6.3) называется векторным параметрическим уравнением прямой в пространстве. В координатной форме уравнение (6.3) равносильно трем уравнениям
Равенства (6.4) называются параметрическими уравнениями прямой в пространстве.
Замечание. Уравнение (6.1) можно было бы получить сразу из параметрических уравнений прямой (6.4), исключив параметр
Уравнение прямой, проходящей через две точки
Постановка задачи: Составить уравнение прямой, проходящей через две точки
Векторы
Равенство (6.5) называется уравнением прямой, походящей через две точки
Общие уравнения прямой в пространстве
Прямую в пространстве можно однозначно определить пересечением двух плоскостей
нормальные векторы
Так как прямая L перпендикулярна векторам
Пример 6.1. Найти канонические и параметрические уравнения прямой, заданной в общем виде
Решение. Находим направляющий вектор данной прямой, если
Пусть
Из условия
,
Взаимное расположение двух прямых в пространстве
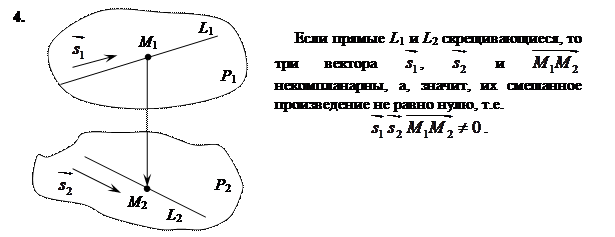
В пространстве две прямые могут: 1) совпадать; 2) быть параллельными; 3) пересекаться; 4) быть скрещивающимися.
Чтобы изучить взаимное расположение двух прямых в пространстве, воспользуемся их каноническими уравнениями.
Пусть даны две прямые:
с направляющими векторами Все возможные ситуации удобно исследуются по изучению взаимного расположения трех векторов:
Угол между двумя прямыми
Углом между двумя прямыми L1 и L2 называют любой из смежных углов, образуемых при их пересечении.
Пусть даны две прямые:
с направляющими векторами Тогда

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 и
и  плоскостей
плоскостей ;
;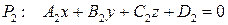
 и
и 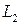 . Угол j между прямыми
. Угол j между прямыми  и
и  , то угол между векторами
, то угол между векторами 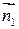 и
и  (
(  ) равен углу j между плоскостями P1 и P2. Тогда равенство
) равен углу j между плоскостями P1 и P2. Тогда равенство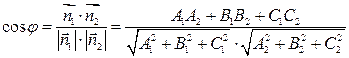 (5.7)
(5.7) и плоскость
и плоскость  . Расстояние от точки
. Расстояние от точки  до плоскости P находится по формуле
до плоскости P находится по формуле . (5.8)
. (5.8) и
и 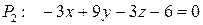 ;
; и
и  .
. и
и  . Так как выполняется условие
. Так как выполняется условие  , то плоскости P1 и P2 параллельны.
, то плоскости P1 и P2 параллельны. и
и  , и найдем z:
, и найдем z: 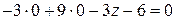 Þ
Þ  . Значит
. Значит  . Найдем расстояние от точки M до плоскости P1:
. Найдем расстояние от точки M до плоскости P1: .
. и
и  . Так как выполняется условие
. Так как выполняется условие  , то плоскости P1 и P2 не являются параллельны. Значит, они пересекаются.
, то плоскости P1 и P2 не являются параллельны. Значит, они пересекаются. .
. .
. . Вектор
. Вектор  называется направляющим вектором прямой.
называется направляющим вектором прямой.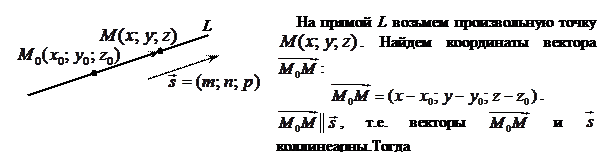
 . (6.1)
. (6.1) и
и 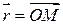 -радиус-векторы точек
-радиус-векторы точек  соответственно. Тогда три вектора
соответственно. Тогда три вектора  ,
,  и
и  связаны соотношением
связаны соотношением . (6.2)
. (6.2) коллинеарны, то существует число
коллинеарны, то существует число 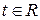 , такое, что
, такое, что  . Тогда из уравнения (6.2) имеем
. Тогда из уравнения (6.2) имеем . (6.3)
. (6.3) ,
,  . Из уравнений (6.4) находим
. Из уравнений (6.4) находим .
. и
и  .
.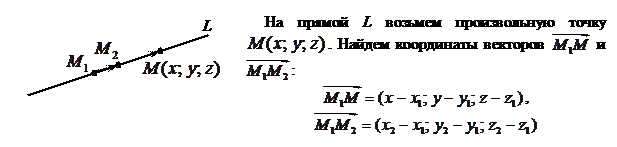
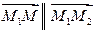 . Тогда
. Тогда . (6.5)
. (6.5) , (6.4)
, (6.4) и
и  которых не параллельны. Уравнения (6.4) называются общими уравнениями прямой в пространстве.
которых не параллельны. Уравнения (6.4) называются общими уравнениями прямой в пространстве. прямой L можно принять векторное произведение
прямой L можно принять векторное произведение  :
: .
. .
. и
и  :
: .
. , тогда получаем и решаем систему уравнений
, тогда получаем и решаем систему уравнений  . Находим точку
. Находим точку  . Используя равенства (6.1) получаем канонические уравнения прямой
. Используя равенства (6.1) получаем канонические уравнения прямой .
. получаем следующие параметрические уравнения прямой L:
получаем следующие параметрические уравнения прямой L: .
. и
и 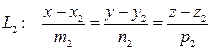
 и
и  соответственно.
соответственно. ,
,  и
и  , где
, где  .
.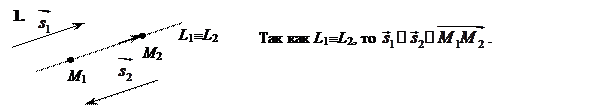
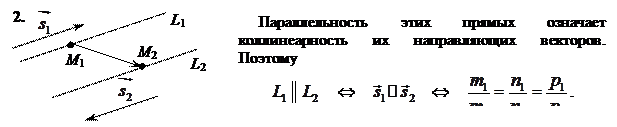

 . (6.5)
. (6.5)