
|
|
Полярная система координатДекартова система координат
Прямоугольная система координат задается двумя взаимно перпендикулярными прямыми – осями, на каждой из которых выбрано положительное направление и задан единичный (масштабный) отрезок. Единицу масштаба обычно берут одинаковой для обеих осей.
Система координат обозначается Рассмотрим произвольную точку Координатами точки
Координата
Повторение некоторых сведений Из раздела «Элементы векторной алгебры»
1. Расстояние между двумя точками Если даны точки
Расстояние между двумя точками находится по следующей формуле:
2. Деление отрезка в заданном отношении Если точка
В частности, если точка
3. Условие коллинеарности двух векторов Если два вектора лежат на одной или параллельных прямых, то они называются коллинеарными, т.е. Пусть
4. Условие перпендикулярности двух векторов Ненулевые векторы
По определению скалярного произведения
Тогда
Преобразование системы координат
Переход от одной системы координат в какую-либо другую называется преобразованием системы координат. Рассмотрим два случая преобразования одной прямоугольной системы координат в другую. Полученные формулы устанавливают зависимость между координатами произвольной точки плоскости в разных системах координат.
1.Параллельный перенос осей координат Пусть на плоскости задана прямоугольная система координат Пусть начало новой системы координат точка
2. Поворот осей координат Под поворотом осей координат понимают такое преобразование координат, при котором обе оси поворачиваются на один и тот же угол, а начало координат и масштаб остается неизменным.
Получаем координаты точки
Тогда
Полученные формулы называются формулами поворота осей. Они позволяют определить старые координаты На плоскости возможны одновременно два вида преобразований: параллельный перенос и поворот осей координат.
Полярная система координат
Декартовая система координат дает удобный, но не единственный способ определения положения точек плоскости при помощи чисел. Другой практически важной системой координат является полярная система координат. Полярная система координат задается точкой
Числа r и j называются полярными координатами точки Для получения всех точек плоскости достаточно полярный угол j ограничить промежутком
Установим связь между прямоугольными и полярными координатами.
Если эти формулы разрешить относительно r и j, то получим следующие формулы:
Чтобы определить величину угла j, лучше использовать формулу
Пример 1.1. Построить точки, заданные полярными координатами:
Найти координаты точек в декартовой системе координат. Решение.
, Пример 1.2. Найти полярные координаты точки Решение.
Учитывая, что ,
Линии на плоскости
Выше были введены координаты точек (декартовы или полярные) на плоскости, т.е. указан способ задания точек с помощью пары чисел. Метод координат в геометрии в том и состоит, что посредством координат точек геометрические объекты задают аналитически с помощью чисел, уравнений, неравенств или их систем. А это дает возможность при решении задач, доказательстве теорем использовать аналитические методы. Метод координат на плоскости используется в геометрии для изучения линий. Линия (или кривая) плоскости задается как множество точек, обладающих некоторым только им присущим геометрическим свойством. Например, прямая, окружность, парабола, синусоида и т.д. Линию (кривую) на плоскости можно задать: 1) уравнением в декартовой системе 2) уравнением в полярной системе координат; 3) параметрически; 4) векторным уравнением.
Так, для того чтобы установить, лежит ли точка Задача о нахождении точек пересечения двух линий, заданных уравнениями
Если эта система не имеет действительных решений, то линии не пересекаются.
где Чтобы перейти от параметрических уравнений линии к уравнению вида
Пример 1.3. Построить линию, которая задана параметрически:
Составить уравнение линии в декартовой и полярной системе координат Решение.
В первом уравнение выразим
В полученное уравнение в декартовой системе координат подставляем
, Пример 1.4. Составить уравнение окружности с центром в начале координат Решение. Напомним, что окружность радиуса
В уравнение окружности в декартовой системе координат вместо
В качестве параметра
Векторное уравнение и параметрические уравнения линии имеют механический смысл. Если точка перемещается на плоскости, то указанные уравнения называются уравнениями движения, а линии – траекторией точки, параметр В аналитической геометрии на плоскости возникают две основные задачи: 1) зная геометрические свойства кривой, найти ее уравнение; 2) зная уравнение кривой, изучить ее форму и свойства.
Приведем примеры некоторых кривых, и укажем их уравнения:
2. УРАВНЕНИЕ ПРЯМОЙ НА ПЛОСКОСТИ
Простейшей из линий является прямая. Разным способам задания прямой соответствуют в прямоугольной системе координат разные виды ее уравнений.
Общее уравнение прямой
Положение прямой Постановка задачи: Составить уравнение прямой, проходящей через точку
Соотношение (2.1) удовлетворяет координатам тех и только тех точек плоскости
Раскрыв скобки в уравнении (2.1), получим
где Общее уравнение прямой (2.2) называется полным, если все его коэффициенты 1) при 2) при 3) при

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|

 , а плоскость, в которой расположена система координат, называют координатной плоскостью.
, а плоскость, в которой расположена система координат, называют координатной плоскостью. плоскости
плоскости 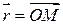 , начало которого совпадает с началом заданной системы координат. Всяка точка
, начало которого совпадает с началом заданной системы координат. Всяка точка  ) называются проекции ее радиус-вектор
) называются проекции ее радиус-вектор  .
. называется абсциссой,
называется абсциссой,  - ординатой точки
- ординатой точки  соответствует единственная точка
соответствует единственная точка 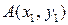 и
и  , то координаты вектора
, то координаты вектора  равны разности соответствующих координат его конца и начала, т.е.
равны разности соответствующих координат его конца и начала, т.е. .
. .
. делит отрезок
делит отрезок 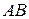 , где
, где  и
и  , в отношении
, в отношении  , то координаты точки
, то координаты точки 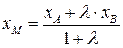 ,
,  .
.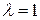 , то
, то ,
,  .
. .
. и
и  . Если
. Если  , где
, где  - некоторое действительное число. Тогда
- некоторое действительное число. Тогда .
. и
и  перпендикулярны (ортогональны) тогда и только тогда, когда их скалярное произведение равно нулю, т.е.
перпендикулярны (ортогональны) тогда и только тогда, когда их скалярное произведение равно нулю, т.е. .
. , где
, где  .
. .
. , при котором меняется положение начала координат, а направление осей и масштаб остается неизменными.
, при котором меняется положение начала координат, а направление осей и масштаб остается неизменными. имеет координаты
имеет координаты  в старой системе координат
в старой системе координат  .
.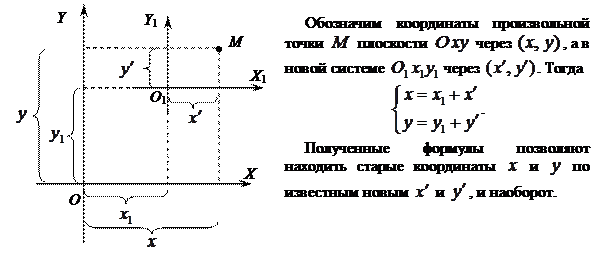
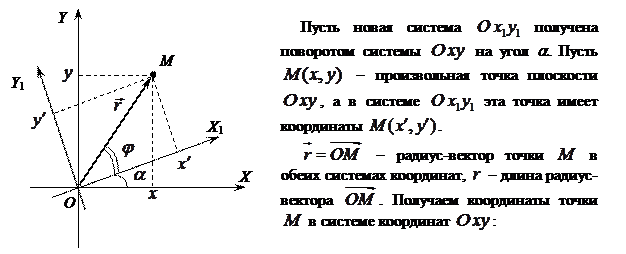
 , или
, или  .
. .
. .
. произвольной точки
произвольной точки  этой же точки
этой же точки 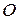 , которая называется полюсом, лучом
, которая называется полюсом, лучом  , называемым полярной осью, и единичным вектором
, называемым полярной осью, и единичным вектором  того же направления, что и луч
того же направления, что и луч 
 , пишут
, пишут 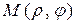 , при этом r называют полярным радиусом, j - полярным углом.
, при этом r называют полярным радиусом, j - полярным углом. (или
(или  ), а полярный радиус -
), а полярный радиус - 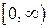 . В этом случае каждой точке плоскости (кроме
. В этом случае каждой точке плоскости (кроме 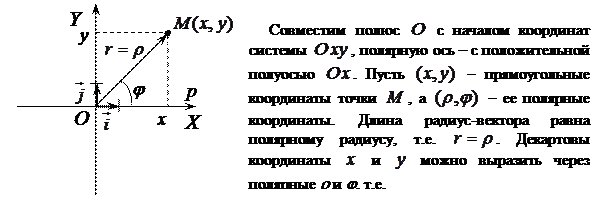
 , где
, где  .
.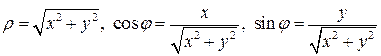 .
. , при этом устанавливается (по знакам
, при этом устанавливается (по знакам  (или
(или  ).
). .
.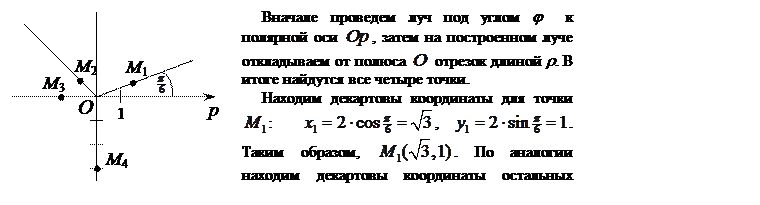
 .
. .
. , следовательно, точка лежит в третьей четверти. Находим r и j:
, следовательно, точка лежит в третьей четверти. Находим r и j: ,
, Þ
Þ  .
. , получаем
, получаем  . Таким образом, получаем точку
. Таким образом, получаем точку  .
. Уравнением линии (или кривой) на плоскости
Уравнением линии (или кривой) на плоскости 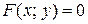 с двумя переменными, которому удовлетворяют координаты
с двумя переменными, которому удовлетворяют координаты  на данной линии, достаточно проверить (не прибегая к геометрическим построениям), удовлетворяют ли координаты точки
на данной линии, достаточно проверить (не прибегая к геометрическим построениям), удовлетворяют ли координаты точки  уравнению этой линии в выбранной системе координат.
уравнению этой линии в выбранной системе координат. и
и  , сводится к отысканию точек, координаты которых удовлетворяют уравнениям обеих линий, т.е. сводится к решению системы двух уравнений с двумя неизвестными:
, сводится к отысканию точек, координаты которых удовлетворяют уравнениям обеих линий, т.е. сводится к решению системы двух уравнений с двумя неизвестными: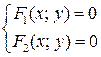 .
. Уравнение
Уравнение 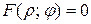 называется уравнением данной линии в полярной системе координат, если координаты любой точки, лежащей на этой линии, и только они, удовлетворяют этому уравнению.
называется уравнением данной линии в полярной системе координат, если координаты любой точки, лежащей на этой линии, и только они, удовлетворяют этому уравнению. Линию на плоскости можно задать параметрически при помощи двух уравнений:
Линию на плоскости можно задать параметрически при помощи двух уравнений: ,
, , лежащей на данной линии, а
, лежащей на данной линии, а  - переменная, называемая параметром; параметр
- переменная, называемая параметром; параметр  .
.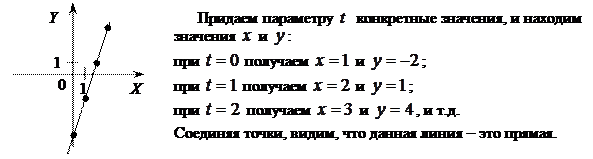
 через
через  Þ
Þ 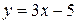 или
или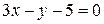 .
. ,
,  , и выражаем
, и выражаем  :
: ;
;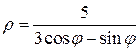 - уравнение данной прямой в полярной системе координат.
- уравнение данной прямой в полярной системе координат. и радиусом
и радиусом  : в декартовой, в полярной системе координат и параметрически.
: в декартовой, в полярной системе координат и параметрически.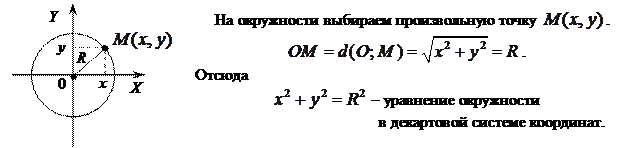
 ;
; ;
; - уравнение окружности в полярной системе координат.
- уравнение окружности в полярной системе координат. - параметрические уравнения окружности. ,
- параметрические уравнения окружности. , Линию на плоскости можно задать векторным уравнением
Линию на плоскости можно задать векторным уравнением  , где
, где  соответствует определенный вектор
соответствует определенный вектор  плоскости. При изменении параметра
плоскости. При изменении параметра 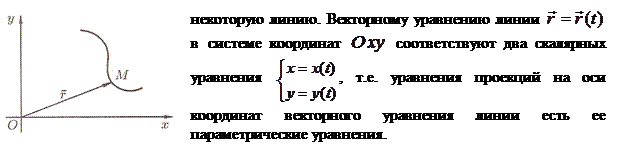
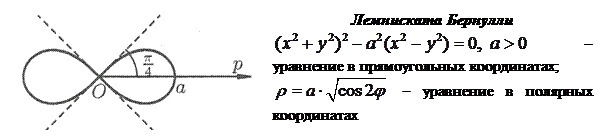

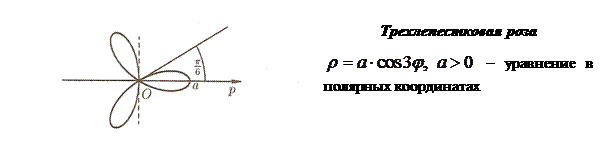


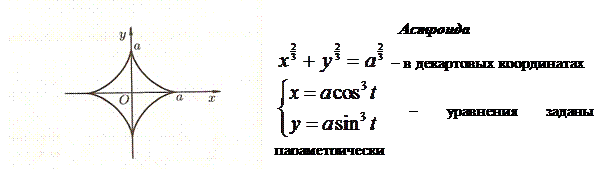
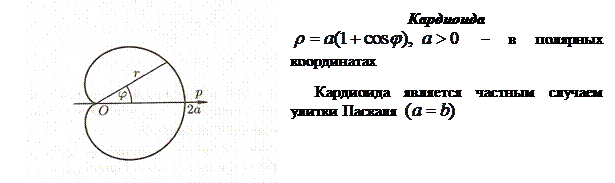

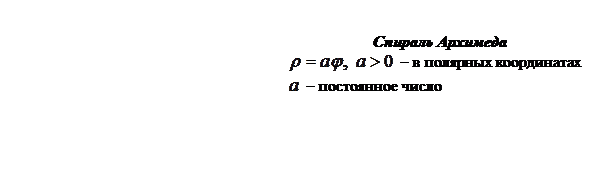
 на плоскости вполне определено, если известны точка
на плоскости вполне определено, если известны точка  , через которую она проходит, и ненулевой вектор
, через которую она проходит, и ненулевой вектор  , перпендикулярный к этой прямой.
, перпендикулярный к этой прямой. называется нормальным вектором прямой.
называется нормальным вектором прямой.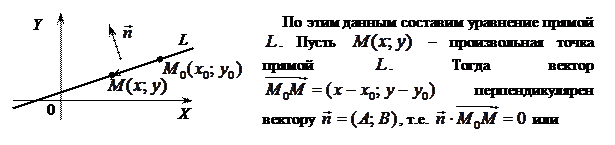
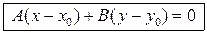 . (2.1)
. (2.1) , (2.2)
, (2.2)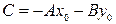 . Уравнение (2.2) называется общим уравнением прямой с нормальным вектором
. Уравнение (2.2) называется общим уравнением прямой с нормальным вектором 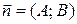 .
. отличны от нуля. Если же хотя бы один из них равен нулю, то уравнение называется неполным. Рассмотрим возможные случаи неполных уравнений:
отличны от нуля. Если же хотя бы один из них равен нулю, то уравнение называется неполным. Рассмотрим возможные случаи неполных уравнений: уравнение
уравнение  определяет прямую, проходящую через начала координат;
определяет прямую, проходящую через начала координат; уравнение
уравнение  Û
Û  определяет прямую, перпендикулярную к вектору
определяет прямую, перпендикулярную к вектору  и параллельную оси
и параллельную оси  . Если
. Если 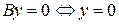 определяет ось
определяет ось  уравнение
уравнение  Û
Û  определяет прямую, перпендикулярную к вектору
определяет прямую, перпендикулярную к вектору  и параллельную оси
и параллельную оси  . Если
. Если  определяет ось
определяет ось