
|
|
Общее уравнение плоскости
Положение плоскости P в пространстве вполне определено, если известны точка Постановка задачи: Составить уравнение плоскости, проходящей через точку
Равенство (5.1) называется уравнением плоскости с нормальным вектором
Раскрыв скобки в уравнении (5.1), получим
где Уравнение (5.2) называется общим уравнением плоскости с нормальным вектором
Общее уравнение плоскости (5.2) называется полным, если все его коэффициенты 1) при 2) при при при 3) при при при
Уравнение плоскости, Параллельной двум данным векторам
Постановка задачи: Составить уравнение плоскости, проходящей через точку
Равенство (5.3) является уравнением плоскости, параллельной векторам
Параметрические уравнения плоскости
Пусть плоскость P определяется двумя неколлинеарными векторами
или
Уравнения (5.4) называются параметрическими уравнениями плоскости.
Уравнение плоскости, Проходящей через три точки
Постановка задачи: Составить уравнение плоскости, проходящей через три точки
или, используя формулу смешанного произведения в координатной форме, получаем следующее равенство
Равенство (5.5) является уравнением плоскости, проходящей через три точки
Уравнение плоскости в отрезках
Пусть плоскость на осях
Далее
Раскрыв определитель, имеем
Равенство (5.6) называется уравнением плоскости в отрезках на осях. Этим уравнением удобно пользоваться при построении плоскости.
Пример 5.1. Составить уравнение плоскости, проходящей через точку Решение. Способ 1. Так как плоскость проходит через ось
По формуле (5.1) составляем уравнение плоскости:
Способ 2. Так как плоскость проходит через ось
Способ 3. Так как плоскость проходит через ось По формуле (5.5) составляем уравнение плоскости:
Способ 4. Так как плоскость проходит через ось По формуле (5.3) составляем уравнение плоскости:
, Пример 5.2. Какие отрезки отсекает на осях координат плоскость
Решение. Приведем данное уравнение к уравнению в отрезках:
Отсюда получаем, что на оси ,
Расположение двух плоскостей
Условия параллельности и перпендикулярности Двух плоскостей
Пусть две плоскости P1 и P2 заданы своими общими уравнениями:
Если плоскости P1 и P2 параллельны, то параллельны и их нормальные векторы
Если

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 , принадлежащая ей, и ненулевой вектор
, принадлежащая ей, и ненулевой вектор  , перпендикулярный к этой плоскости.
, перпендикулярный к этой плоскости.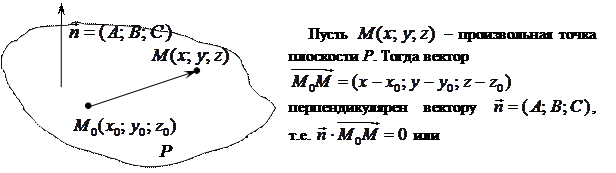
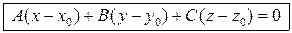 . (5.1)
. (5.1) , (5.2)
, (5.2)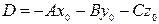 .
.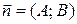 .
. и
и  отличны от нуля. Если же хотя бы один из них равен нулю, то уравнение называется неполным. Рассмотрим возможные случаи неполных уравнений:
отличны от нуля. Если же хотя бы один из них равен нулю, то уравнение называется неполным. Рассмотрим возможные случаи неполных уравнений: уравнение
уравнение  определяет плоскость, проходящую через начала координат;
определяет плоскость, проходящую через начала координат; уравнение
уравнение 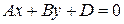 с нормальным вектором
с нормальным вектором  , перпендикулярным к оси
, перпендикулярным к оси  , определяет плоскость, параллельную оси
, определяет плоскость, параллельную оси  уравнение
уравнение  с нормальным вектором
с нормальным вектором 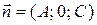 , перпендикулярным к оси
, перпендикулярным к оси  , определяет плоскость, параллельную оси
, определяет плоскость, параллельную оси  уравнение
уравнение  с нормальным вектором
с нормальным вектором  , перпендикулярным к оси
, перпендикулярным к оси  , определяет плоскость, параллельную оси
, определяет плоскость, параллельную оси 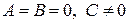 уравнение
уравнение  Û
Û  с нормальным вектором
с нормальным вектором 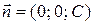 параллельным оси
параллельным оси  и пересекающую ось
и пересекающую ось 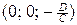 . Если
. Если  определяет плоскость
определяет плоскость  уравнение
уравнение  Û
Û 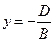 с нормальным вектором
с нормальным вектором  параллельным оси
параллельным оси  и пересекающую ось
и пересекающую ось  . Если
. Если 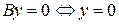 определяет плоскость
определяет плоскость  уравнение
уравнение  Û
Û  с нормальным вектором
с нормальным вектором  параллельным оси
параллельным оси  и пересекающую ось
и пересекающую ось  . Если
. Если  определяет плоскость
определяет плоскость 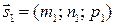 и
и  , неколлинеарных между собой.
, неколлинеарных между собой.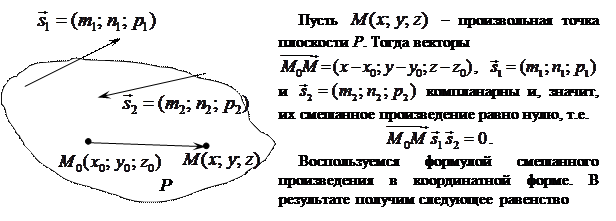
 . (5.3)
. (5.3) .
.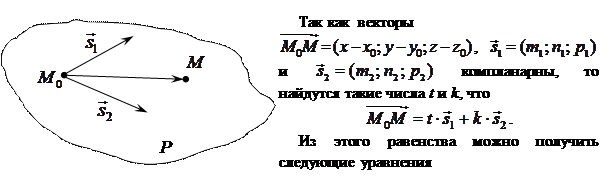
 ,
,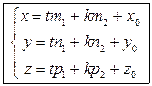 . (5.4)
. (5.4) ,
,  и
и  .
.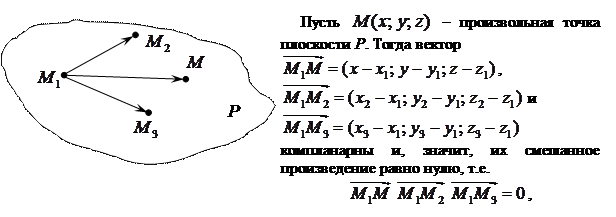
 . (5.5)
. (5.5) ,
,  и
и  соответственно.
соответственно.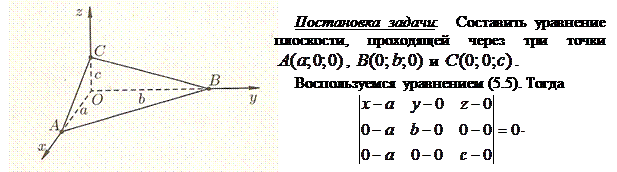
 .
. , т.е.
, т.е.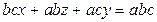 или
или . (5.6)
. (5.6)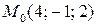 и ось
и ось  . В этой плоскости лежит и вектор
. В этой плоскости лежит и вектор  .
.
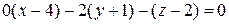 Þ
Þ  .
. . Так как точка
. Так как точка  принадлежит плоскости, то координаты этой точки удовлетворяют уравнению искомой плоскости, т.е.
принадлежит плоскости, то координаты этой точки удовлетворяют уравнению искомой плоскости, т.е.  Þ
Þ  , где
, где  . Таким образом уравнение плоскости примет вид:
. Таким образом уравнение плоскости примет вид: Þ
Þ  и
и  , принадлежащие оси
, принадлежащие оси  Þ
Þ  Þ
Þ  .
. Þ
Þ  Þ
Þ  .
. , на оси
, на оси 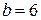 , на оси
, на оси 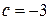 .
. ;
;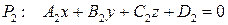 .
. и
и  . Отсюда, учитывая условие параллельности векторов, получаем условие параллельности двух плоскостей:
. Отсюда, учитывая условие параллельности векторов, получаем условие параллельности двух плоскостей: Þ
Þ  Û
Û  .
. , то
, то  и, значит, условие перпендикулярности двух плоскостей имеет вид:
и, значит, условие перпендикулярности двух плоскостей имеет вид: Û
Û  .
.