Расстояние от точки до прямой
Постановка задачи: Пусть задана прямая L уравнением  точка точка  . Требуется найти расстояние от точки . Требуется найти расстояние от точки  до прямой L. до прямой L.

 . .
Так как точка  принадлежит прямой L, то принадлежит прямой L, то 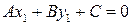 , т.е. , т.е.  . Поэтому . Поэтому
 , (2.9) , (2.9)
что и требовалось получить.
,
3. ЛИНИИ ВТОРОГО ПОРЯДКА
Прямая линия описывается общим уравнением  , в которое текущие координаты , в которое текущие координаты  и и  входят с первой степенью. Такие линии называются линейными или уравнениями первого порядка. Уравнения линий (кривых) на плоскости, содержащие, кроме первых степеней текущих координат входят с первой степенью. Такие линии называются линейными или уравнениями первого порядка. Уравнения линий (кривых) на плоскости, содержащие, кроме первых степеней текущих координат  и и  , квадраты этих координат или их произведение , квадраты этих координат или их произведение 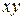 , относятся к уравнениям кривых второго порядка. , относятся к уравнениям кривых второго порядка.
Определение 3.1. Линии (кривые), заданные уравнением вида
 , (3.1) , (3.1)
где коэффициенты уравнения являются действительными числами и, по крайней мере, одно из чисел 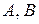 или или  отличны от нуля, называются линиями (кривыми) второго порядка. отличны от нуля, называются линиями (кривыми) второго порядка.
Окружность
Простейшей кривой второго порядка является окружность.
Определение 3.2. Окружностью радиуса  с центром в точке с центром в точке 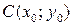 называется множество всех точек плоскости, равноудаленных от точки называется множество всех точек плоскости, равноудаленных от точки  . .

 . (3.2) . (3.2)
Уравнение (3.2) называется каноническим уравнением окружности.
Например, если  - центр окружности, - центр окружности,  , то уравнение окружности примет вид: , то уравнение окружности примет вид: 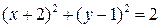 . .
Пример 3.1. Доказать, что уравнение вида  является уравнением окружности. является уравнением окружности.
Доказательство. Преобразуем данное уравнение, выделив полные квадраты относительно переменных  и и  : :
 . .
Следовательно,
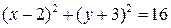
- есть каноническое уравнение окружности с центром  и радиусом и радиусом  . .
,
Эллипс
Определение 3.3. Эллипсом называется множество всех точек плоскости, сумма от каждой из которых до двух данных точек этой плоскости, называемых фокусами, есть величина постоянная, большая, чем расстояние между фокусами.
Обозначим фокусы через  и и 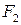 , расстояние между ними через , расстояние между ними через 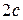 , т.е. , т.е. 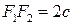 , которое называется междуфокусным расстоянием эллипса. Сумма расстояний от произвольной точки эллипса до фокусов обозначим через , которое называется междуфокусным расстоянием эллипса. Сумма расстояний от произвольной точки эллипса до фокусов обозначим через  , где , где  . .

Пусть  - произвольная точка эллипса. Обозначим - произвольная точка эллипса. Обозначим  и и  . Величины . Величины  и и  называются фокальными радиусами точки называются фокальными радиусами точки  эллипса. По определению эллипса эллипса. По определению эллипса 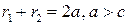 . Так как . Так как  и и  , то из уравнения , то из уравнения 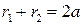 получаем получаем
 . (3.3) . (3.3)
Это и есть уравнение эллипса в выбранной системе координат.
Преобразуем уравнение (3.3) к более простому виду следующим образом:
 , ,
 , ,
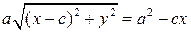 , ,
 , ,
 . .
Так как  , то , то  . Положим . Положим  . Тогда последнее уравнение примет вид . Тогда последнее уравнение примет вид

или
 . (3.4) . (3.4)
Уравнение (3.4) называется каноническим уравнением эллипса. Числа 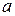 и и  называются соответственно большой и малой полуосями эллипса. называются соответственно большой и малой полуосями эллипса.
Чтобы установить форму эллипса и построить его в прямоугольной системе координат  , проведем исследование его канонического уравнения. , проведем исследование его канонического уравнения.
1. Уравнение (3.4) содержит  и и  только в четной степени, поэтому если точка только в четной степени, поэтому если точка  принадлежит эллипсу, то ему принадлежат точки принадлежит эллипсу, то ему принадлежат точки  , ,  и и  . Отсюда следует, что эллипс симметричен относительно осей . Отсюда следует, что эллипс симметричен относительно осей  и и  , а также относительно начала координат , а также относительно начала координат  , который называют центром эллипса. , который называют центром эллипса.
2. Найдем точки пересечения эллипса с осями координат. Положив в уравнение (3.4)  , находим две точки , находим две точки  и и  , в которых эллипс пересекает ось , в которых эллипс пересекает ось  . Положив . Положив  , находим точки пересечения эллипса с осью , находим точки пересечения эллипса с осью  : :  и и  . Точки . Точки  называются вершинами эллипса. называются вершинами эллипса.
3. Из уравнения (3.4) следует, что каждое слагаемое в левой части не превосходит единицы, т.е. имеют место неравенства  и и  или или  и и  . Следовательно, все точки эллипса лежат внутри прямоугольника, образованного прямыми . Следовательно, все точки эллипса лежат внутри прямоугольника, образованного прямыми  и и  . .
4. В уравнении (3.4) сумма неотрицательных слагаемых 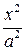 и и  равна единице. Следовательно, при возрастании одного слагаемого другое будет уменьшаться, т.е. если равна единице. Следовательно, при возрастании одного слагаемого другое будет уменьшаться, т.е. если 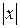 возрастает, то возрастает, то  уменьшается и наоборот. уменьшается и наоборот.
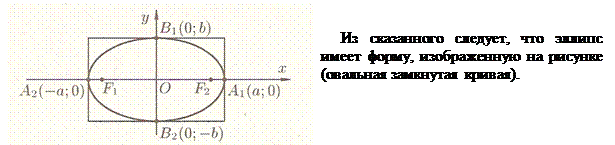
Есть и другие способы построения эллипса.
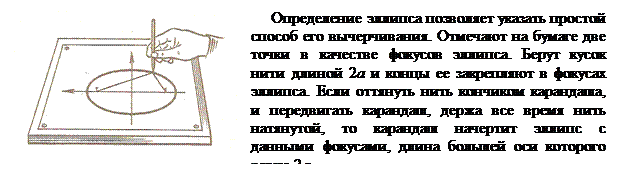
Рассмотрим способ построения точек эллипса с помощью циркуля и линейки, если заданы его оси  и и 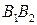 . .
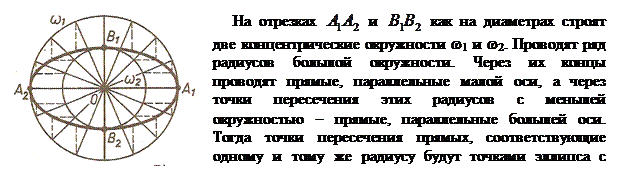
Эллипс можно задать не только каноническим уравнением, но и параметрическими уравнениями.
Сделав в каноническом уравнении эллипса замену переменных  , получаем уравнение окружности , получаем уравнение окружности  . Параметрические уравнения этой окружности имеют вид . Параметрические уравнения этой окружности имеют вид  . Далее находим . Далее находим
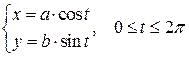 (3.5) (3.5)
Уравнения (3.5) называются параметрическими уравнениями эллипса.
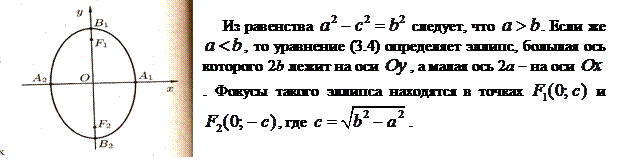
В качестве характеристики формы эллипса используется отношение  . .
Обозначим  (e - «эпсилон»). Это число называется эксцентриситетом эллипса. Так как (e - «эпсилон»). Это число называется эксцентриситетом эллипса. Так как 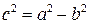 , то , то
 и и
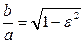
Отсюда следует, что при 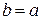 (в этом случае эллипс превращается в окружность (в этом случае эллипс превращается в окружность  ) эксцентриситет ) эксцентриситет 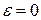 . Так как для эллипса . Так как для эллипса  , то , то  . Таким образом, для эллипса . Таким образом, для эллипса 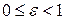 . При . При  эллипс становится более вытянутым вдоль оси эллипс становится более вытянутым вдоль оси  . .
Через эксцентриситет e можно выразить фокальные радиусы  и и  любой его точки любой его точки  . Действительно, . Действительно,  . Используя формулы . Используя формулы  и (3.4) можно получить и (3.4) можно получить
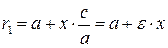 . .
По аналогии получаем  . .
При изучении эллипса большую роль играют две прямые  , которые называются директрисами эллипса. Директриса , которые называются директрисами эллипса. Директриса 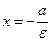 называется левой, а называется левой, а  - правой. Директрисы эллипса обладают свойством, которое сформулируем в виде теоремы (без доказательства). - правой. Директрисы эллипса обладают свойством, которое сформулируем в виде теоремы (без доказательства).

Пример 3.2. Большая ось эллипса равна 12, а директрисами его служат прямые  . Найти уравнение эллипса и его эксцентриситет. . Найти уравнение эллипса и его эксцентриситет.
Решение. По условию  . Из уравнений директрис находим . Из уравнений директрис находим  : :
 . .
Тогда 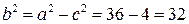 . Следователь, искомое уравнение эллипса есть . Следователь, искомое уравнение эллипса есть
 . .
Эксцентриситет его  . .
,
Замечание. Если центр эллипса с полуосями 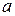 и и  смещен в точку смещен в точку  , то его каноническое уравнение имеет вид , то его каноническое уравнение имеет вид
 . .
Гипербола
Определение 3.4. Гиперболой называется множество всех точек плоскости, модуль разности расстояний от каждой из которых до двух данных точек этой плоскости, называемых фокусами, есть величина постоянная, меньшая, чем расстояние между фокусами.
Обозначим фокусы через  и и 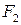 , расстояние между ними через , расстояние между ними через 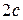 , т.е. , т.е. 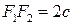 . Модуль разности расстояний от каждой точки гиперболы до фокусов обозначим через . Модуль разности расстояний от каждой точки гиперболы до фокусов обозначим через  , где , где  . .

Пусть  - произвольная точка гиперболы. Обозначим - произвольная точка гиперболы. Обозначим  и и  , которые называются фокальными радиусами точки , которые называются фокальными радиусами точки  . По определению гиперболы . По определению гиперболы  или или 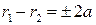 . Так как . Так как  и и  , то из уравнения , то из уравнения 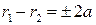 получаем получаем
 . .
После упрощений, как это было сделано при выводе уравнения эллипса, получим каноническое уравнение гиперболы
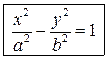 . (3.6) . (3.6)
где  . Числа . Числа 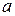 и и  называются соответственно действительной и мнимой полуосями гиперболы. называются соответственно действительной и мнимой полуосями гиперболы.
Чтобы установить форму гиперболы и построить ее в прямоугольной системе координат  , проведем исследование ее канонического уравнения. , проведем исследование ее канонического уравнения.
1. Уравнение (3.6) содержит  и и  только в четной степени. Отсюда следует, что эллипс симметричен относительно осей только в четной степени. Отсюда следует, что эллипс симметричен относительно осей  и и  , а также относительно начала координат , а также относительно начала координат  , который называют центром гиперболы. , который называют центром гиперболы.
2. Найдем точки пересечения эллипса с осями координат. Положив в уравнение (3.6)  , находим две точки , находим две точки  и и  , в которых эллипс пересекает ось , в которых эллипс пересекает ось  , которая называется действительной осью гиперболы. Положив , которая называется действительной осью гиперболы. Положив  , получаем , получаем 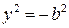 - уравнение, которое не имеет действительных решений. Значит, гипербола ось - уравнение, которое не имеет действительных решений. Значит, гипербола ось  не пересекает. Ось не пересекает. Ось  называется мнимой осью. Точки называется мнимой осью. Точки 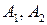 называются вершинами гиперболы. Прямоугольник со сторонами называются вершинами гиперболы. Прямоугольник со сторонами  и и  называется основным прямоугольником гиперболы. называется основным прямоугольником гиперболы.
3. Из уравнения (3.6) следует, что уменьшаемое 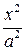 не меньше единицы, т.е. не меньше единицы, т.е.  или или  . Это означает, что точки гиперболы расположены справа от прямой . Это означает, что точки гиперболы расположены справа от прямой 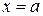 (правая ветвь гиперболы) и слева от прямой (правая ветвь гиперболы) и слева от прямой 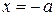 (левая ветвь гиперболы). (левая ветвь гиперболы).
4. Из уравнения (3.6) гиперболы видно, что когда 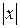 возрастает, то и возрастает, то и  возрастает. Это следует из того, что разность возрастает. Это следует из того, что разность  сохраняет постоянное значений, равное единице. сохраняет постоянное значений, равное единице.
5. Две прямые  и и  являются асимптотами гиперболы. являются асимптотами гиперболы.
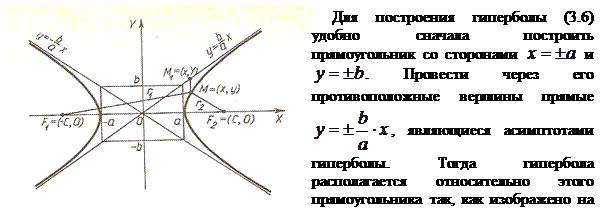
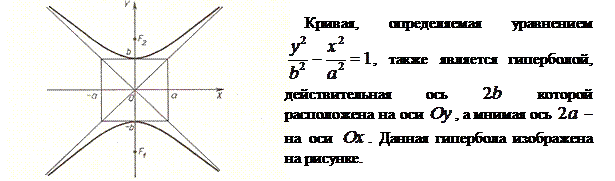
Как и у эллипса, у гиперболы также рассматриваются эксцентриситет и директрисы.
Число  называется эксцентриситетом гиперболы. Так как называется эксцентриситетом гиперболы. Так как  , то , то
 и и  . .
Отсюда следует, что для гиперболы эксцентриситет  . Через эксцентриситет e можно выразить фокальные радиусы . Через эксцентриситет e можно выразить фокальные радиусы  и и  любой его точки любой его точки  . Для фокальных радиусов точки . Для фокальных радиусов точки  гиперболы получаем формулы гиперболы получаем формулы
 и и  . .
При изучении гиперболы большую роль играют две прямые 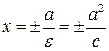 , которые называются директрисами гиперболы. Так как для гиперболы , которые называются директрисами гиперболы. Так как для гиперболы  , то , то  . Это означает, что правая директриса расположена между центром и правой вершиной гиперболы, а левая – между центром и левой вершиной. . Это означает, что правая директриса расположена между центром и правой вершиной гиперболы, а левая – между центром и левой вершиной.
Директрисы гиперболы обладают тем же свойством, что и директрисы эллипса.

Замечание. Если центр гиперболы смещен в точку  , то ее каноническое уравнение имеет вид , то ее каноническое уравнение имеет вид
 или или 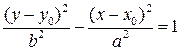 , ,
а асимптотами служат прямые вида
 . .
Парабола
Определение 3.5. Параболой называется множество точек плоскости, равноудаленных от данной точки, называемой фокусом параболы, и данной прямой, называемой ее директрисой.
Расстояние от фокуса  до директрисы называется фокальным параметром параболы и обозначается до директрисы называется фокальным параметром параболы и обозначается  . .
Для вывода уравнения параболы выберем систему координат  так, чтобы ось так, чтобы ось  прошла через фокус прошла через фокус  перпендикулярно директрисе в направлении от директрисы к перпендикулярно директрисе в направлении от директрисы к  , а начало координат , а начало координат  расположим посередине между фокусом и директрисой. расположим посередине между фокусом и директрисой.
В выбранной системе координат фокус  , а уравнение директрисы имеет вид , а уравнение директрисы имеет вид  . Пусть . Пусть  - произвольная точка параболы. Соединим точку - произвольная точка параболы. Соединим точку  с с  , где , где  называется фокальным радиусом точки называется фокальным радиусом точки  . Проведем отрезок . Проведем отрезок 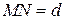 перпендикулярно директрисе. Согласно определению параболы перпендикулярно директрисе. Согласно определению параболы  . По формуле расстояния между двумя точками находим: . По формуле расстояния между двумя точками находим:
| | 
 , а , а  . .
Следовательно,
 . .
Возведя обе части уравнения в квадрат, получим
 , ,
т.е.
 . (3.7) . (3.7)
Уравнение (3.7) называется каноническим уравнением параболы.
Для любой точки  параболы параболы  . Так как для точек эллипса и гиперболы . Так как для точек эллипса и гиперболы  , то для параболы естественно считать эксцентриситет , то для параболы естественно считать эксцентриситет  . .
Чтобы установить форму параболы и построить ее в прямоугольной системе координат  , проведем исследование ее канонического уравнения. , проведем исследование ее канонического уравнения.
1. В уравнении (3.7) переменная  входит в четной степени, значит, парабола симметрична относительна оси входит в четной степени, значит, парабола симметрична относительна оси  ; ось ; ось  является осью симметрии параболы. является осью симметрии параболы.
2. Так как 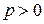 , то из (3.7) следует, что , то из (3.7) следует, что  . Следовательно, парабола расположена справа от оси . Следовательно, парабола расположена справа от оси  . .
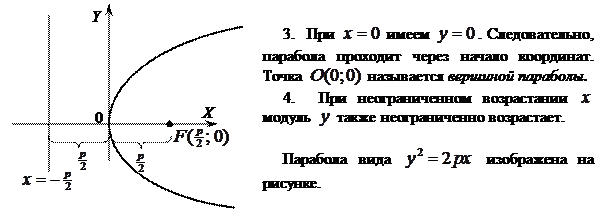
Уравнения вида 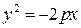 , ,  и и  также определяют параболы, которые изображены на рисунке. также определяют параболы, которые изображены на рисунке.
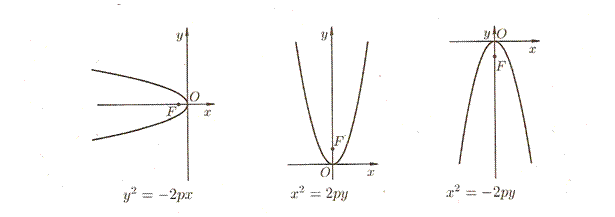
Нетрудно показать, что график квадратного трехчлена  , где , где  , ,  и и  любые действительные числа, представляет собой параболу в смысле приведенного выше ее определения. любые действительные числа, представляет собой параболу в смысле приведенного выше ее определения.
Замечание. Если вершина параболы  или или  смещена в точку смещена в точку  , то ее каноническое уравнение имеет вид , то ее каноническое уравнение имеет вид
 или или  . .
Для параболы  , осью симметрии служит прямая , осью симметрии служит прямая 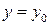 , а фокус имеет координаты , а фокус имеет координаты 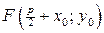 , директриса описывается уравнением , директриса описывается уравнением  . .
Аналогично для параболы 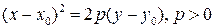 , осью симметрии служит прямая , осью симметрии служит прямая  , а фокус имеет координаты , а фокус имеет координаты  , директриса описывается уравнением , директриса описывается уравнением  . .
Пример 3.3. Установить вид кривой второго порядка, заданной уравнением
 . .
Решение. Выделим в этом уравнении полные квадраты:
 Þ Þ
 Þ Þ
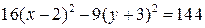 Þ Þ
 . .
Данное уравнение определяет гиперболу с центром в точке 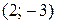 ; действительная полуось ; действительная полуось  , мнимая полуось , мнимая полуось  ; эксцентриситет ; эксцентриситет
 . .
,
4. УРАВНЕНИЯ ПОВЕРХНОСТИ И
ЛИНИИ В ПРОСТРАНСТВЕ
Не нашли, что искали? Воспользуйтесь поиском по сайту:
©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|



 точка
точка  . Требуется найти расстояние от точки
. Требуется найти расстояние от точки  до прямой L.
до прямой L.
 .
. принадлежит прямой L, то
принадлежит прямой L, то 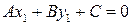 , т.е.
, т.е.  . Поэтому
. Поэтому , (2.9)
, (2.9) и
и  входят с первой степенью. Такие линии называются линейными или уравнениями первого порядка. Уравнения линий (кривых) на плоскости, содержащие, кроме первых степеней текущих координат
входят с первой степенью. Такие линии называются линейными или уравнениями первого порядка. Уравнения линий (кривых) на плоскости, содержащие, кроме первых степеней текущих координат 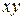 , относятся к уравнениям кривых второго порядка.
, относятся к уравнениям кривых второго порядка. , (3.1)
, (3.1)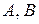 или
или  отличны от нуля, называются линиями (кривыми) второго порядка.
отличны от нуля, называются линиями (кривыми) второго порядка. с центром в точке
с центром в точке 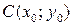 называется множество всех точек плоскости, равноудаленных от точки
называется множество всех точек плоскости, равноудаленных от точки 
 . (3.2)
. (3.2) - центр окружности,
- центр окружности,  , то уравнение окружности примет вид:
, то уравнение окружности примет вид: 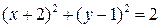 .
. является уравнением окружности.
является уравнением окружности. .
.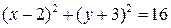
 и радиусом
и радиусом  .
. и
и 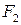 , расстояние между ними через
, расстояние между ними через 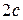 , т.е.
, т.е. 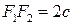 , которое называется междуфокусным расстоянием эллипса. Сумма расстояний от произвольной точки эллипса до фокусов обозначим через
, которое называется междуфокусным расстоянием эллипса. Сумма расстояний от произвольной точки эллипса до фокусов обозначим через  , где
, где  .
.
 - произвольная точка эллипса. Обозначим
- произвольная точка эллипса. Обозначим  и
и  . Величины
. Величины  и
и  называются фокальными радиусами точки
называются фокальными радиусами точки  эллипса. По определению эллипса
эллипса. По определению эллипса 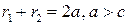 . Так как
. Так как  и
и  , то из уравнения
, то из уравнения 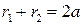 получаем
получаем . (3.3)
. (3.3) ,
, ,
,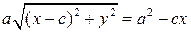 ,
, ,
, .
. , то
, то  . Положим
. Положим  . Тогда последнее уравнение примет вид
. Тогда последнее уравнение примет вид
 . (3.4)
. (3.4)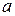 и
и  называются соответственно большой и малой полуосями эллипса.
называются соответственно большой и малой полуосями эллипса. , проведем исследование его канонического уравнения.
, проведем исследование его канонического уравнения. принадлежит эллипсу, то ему принадлежат точки
принадлежит эллипсу, то ему принадлежат точки  ,
,  и
и  . Отсюда следует, что эллипс симметричен относительно осей
. Отсюда следует, что эллипс симметричен относительно осей  и
и  , а также относительно начала координат
, а также относительно начала координат  , который называют центром эллипса.
, который называют центром эллипса. , находим две точки
, находим две точки  и
и  , в которых эллипс пересекает ось
, в которых эллипс пересекает ось  , находим точки пересечения эллипса с осью
, находим точки пересечения эллипса с осью  и
и  . Точки
. Точки  называются вершинами эллипса.
называются вершинами эллипса. и
и  или
или  и
и  . Следовательно, все точки эллипса лежат внутри прямоугольника, образованного прямыми
. Следовательно, все точки эллипса лежат внутри прямоугольника, образованного прямыми  и
и  .
.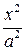 и
и  равна единице. Следовательно, при возрастании одного слагаемого другое будет уменьшаться, т.е. если
равна единице. Следовательно, при возрастании одного слагаемого другое будет уменьшаться, т.е. если 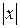 возрастает, то
возрастает, то  уменьшается и наоборот.
уменьшается и наоборот.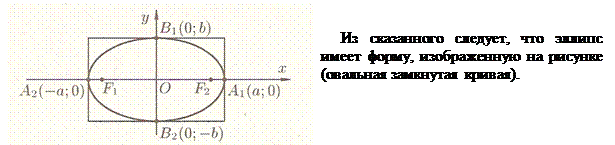
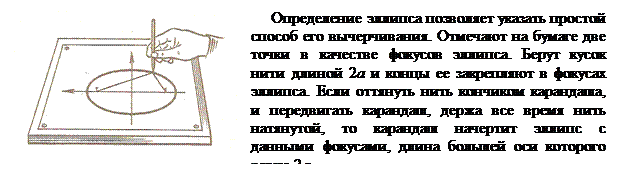
 и
и 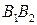 .
.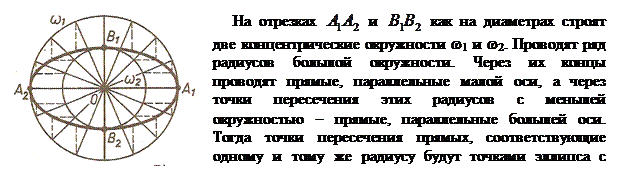
 , получаем уравнение окружности
, получаем уравнение окружности  . Параметрические уравнения этой окружности имеют вид
. Параметрические уравнения этой окружности имеют вид  . Далее находим
. Далее находим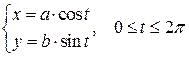 (3.5)
(3.5)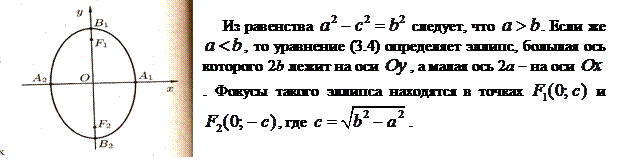
 .
. (e - «эпсилон»). Это число называется эксцентриситетом эллипса. Так как
(e - «эпсилон»). Это число называется эксцентриситетом эллипса. Так как 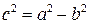 , то
, то и
и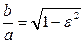
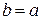 (в этом случае эллипс превращается в окружность
(в этом случае эллипс превращается в окружность  ) эксцентриситет
) эксцентриситет 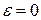 . Так как для эллипса
. Так как для эллипса  , то
, то  . Таким образом, для эллипса
. Таким образом, для эллипса 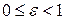 . При
. При  эллипс становится более вытянутым вдоль оси
эллипс становится более вытянутым вдоль оси  . Используя формулы
. Используя формулы  и (3.4) можно получить
и (3.4) можно получить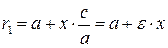 .
. .
. , которые называются директрисами эллипса. Директриса
, которые называются директрисами эллипса. Директриса 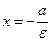 называется левой, а
называется левой, а  - правой. Директрисы эллипса обладают свойством, которое сформулируем в виде теоремы (без доказательства).
- правой. Директрисы эллипса обладают свойством, которое сформулируем в виде теоремы (без доказательства).
 . Найти уравнение эллипса и его эксцентриситет.
. Найти уравнение эллипса и его эксцентриситет. . Из уравнений директрис находим
. Из уравнений директрис находим  :
: .
.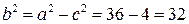 . Следователь, искомое уравнение эллипса есть
. Следователь, искомое уравнение эллипса есть .
. .
. , то его каноническое уравнение имеет вид
, то его каноническое уравнение имеет вид .
. .
.
 или
или 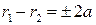 . Так как
. Так как  .
.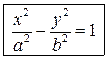 . (3.6)
. (3.6) . Числа
. Числа 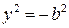 - уравнение, которое не имеет действительных решений. Значит, гипербола ось
- уравнение, которое не имеет действительных решений. Значит, гипербола ось 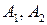 называются вершинами гиперболы. Прямоугольник со сторонами
называются вершинами гиперболы. Прямоугольник со сторонами  называется основным прямоугольником гиперболы.
называется основным прямоугольником гиперболы. или
или  . Это означает, что точки гиперболы расположены справа от прямой
. Это означает, что точки гиперболы расположены справа от прямой 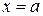 (правая ветвь гиперболы) и слева от прямой
(правая ветвь гиперболы) и слева от прямой 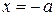 (левая ветвь гиперболы).
(левая ветвь гиперболы). сохраняет постоянное значений, равное единице.
сохраняет постоянное значений, равное единице. и
и  являются асимптотами гиперболы.
являются асимптотами гиперболы.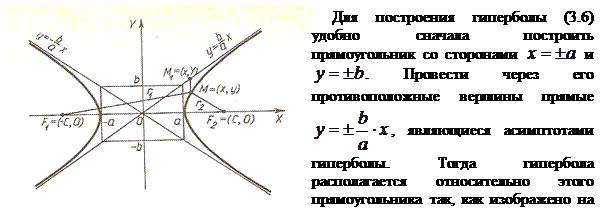
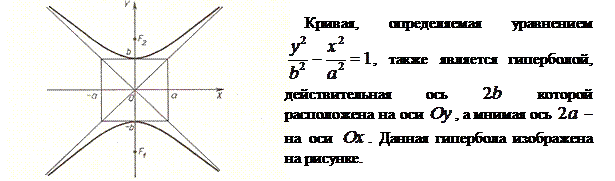
 , то
, то и
и  .
. . Через эксцентриситет e можно выразить фокальные радиусы
. Через эксцентриситет e можно выразить фокальные радиусы  и
и  .
.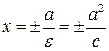 , которые называются директрисами гиперболы. Так как для гиперболы
, которые называются директрисами гиперболы. Так как для гиперболы  . Это означает, что правая директриса расположена между центром и правой вершиной гиперболы, а левая – между центром и левой вершиной.
. Это означает, что правая директриса расположена между центром и правой вершиной гиперболы, а левая – между центром и левой вершиной.
 или
или 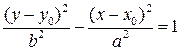 ,
, .
. до директрисы называется фокальным параметром параболы и обозначается
до директрисы называется фокальным параметром параболы и обозначается  .
. расположим посередине между фокусом и директрисой.
расположим посередине между фокусом и директрисой. , а уравнение директрисы имеет вид
, а уравнение директрисы имеет вид  . Пусть
. Пусть  называется фокальным радиусом точки
называется фокальным радиусом точки 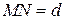 перпендикулярно директрисе. Согласно определению параболы
перпендикулярно директрисе. Согласно определению параболы  . По формуле расстояния между двумя точками находим:
. По формуле расстояния между двумя точками находим:
 , а
, а  .
. .
. ,
, . (3.7)
. (3.7) . Так как для точек эллипса и гиперболы
. Так как для точек эллипса и гиперболы  , то для параболы естественно считать эксцентриситет
, то для параболы естественно считать эксцентриситет  .
.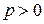 , то из (3.7) следует, что
, то из (3.7) следует, что  . Следовательно, парабола расположена справа от оси
. Следовательно, парабола расположена справа от оси 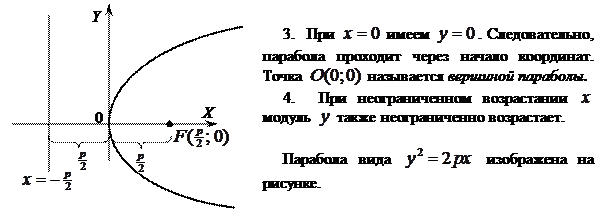
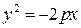 ,
,  и
и  также определяют параболы, которые изображены на рисунке.
также определяют параболы, которые изображены на рисунке.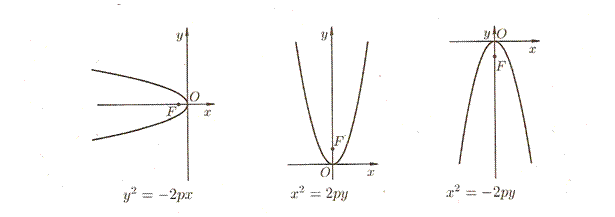
 , где
, где  ,
,  и
и  или
или  или
или  .
. , осью симметрии служит прямая
, осью симметрии служит прямая 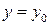 , а фокус имеет координаты
, а фокус имеет координаты 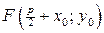 , директриса описывается уравнением
, директриса описывается уравнением  .
.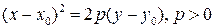 , осью симметрии служит прямая
, осью симметрии служит прямая  , а фокус имеет координаты
, а фокус имеет координаты  , директриса описывается уравнением
, директриса описывается уравнением  .
. .
. Þ
Þ Þ
Þ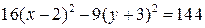 Þ
Þ .
.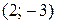 ; действительная полуось
; действительная полуось  , мнимая полуось
, мнимая полуось  ; эксцентриситет
; эксцентриситет .
.