Уравнение прямой с угловым коэффициентом
Уравнение вида
 (2.3) (2.3)
называется уравнением прямой с угловым коэффициентом k.
Уравнение (2.3) можно получить из общего уравнения (2.2) при  . Действительно, из (2.2) имеем . Действительно, из (2.2) имеем  . Обозначив . Обозначив 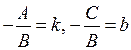 , придем к уравнению (2.3). , придем к уравнению (2.3).
Выясним геометрический смысл углового коэффициента  прямой прямой  . .
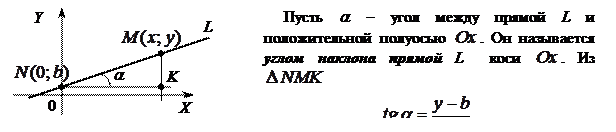
или
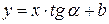 . .
Итак,  и и  . Сравнивая два уравнения, получаем . Сравнивая два уравнения, получаем  . .
Угловой коэффициент k прямой  численно равен тангенсу угла наклона этой прямой к оси численно равен тангенсу угла наклона этой прямой к оси  , т.е. , т.е.  . .
Постановка задачи: Составить уравнение прямой, проходящей через точку  с угловым коэффициентом k. с угловым коэффициентом k.
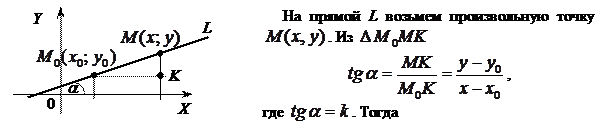
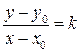 , или , или
 . (2.4) . (2.4)
Равенство (2.4) называется уравнением прямой с угловым коэффициентом, проходящей через заданную точку  . .
Каноническое уравнение прямой
Постановка задачи: Составить уравнение прямой, проходящей через точку  , и параллельной вектору , и параллельной вектору  . Вектор . Вектор  называется направляющим вектором прямой. называется направляющим вектором прямой.
На прямой L возьмем произвольную точку  . Найдем координаты вектора . Найдем координаты вектора  : :
 . .
 . Тогда . Тогда
 . (2.5) . (2.5)
| | 
Равенство (2.5) называется каноническим уравнением прямой на плоскости.
Параметрические уравнения прямой
Так как векторы  и и  коллинеарные, то существует такое число коллинеарные, то существует такое число 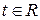 , что , что  . Значит, . Значит,
 , или , или
 . (2.6) . (2.6)
Уравнение (2.6) называется параметрическими уравнениями прямой на плоскости, проходящей через точку  с направляющим вектором с направляющим вектором  . .
Уравнение прямой, проходящей через две точки
Постановка задачи: Составить уравнение прямой, проходящей через две точки  и и  . .
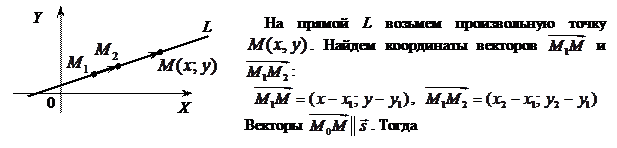
 . (2.7) . (2.7)
Равенство (2.7) называется уравнением прямой, походящей через две точки  и и  . .
Уравнение прямой в отрезках
Пусть прямая L на осях координат  и и  отсекает отрезки длиной отсекает отрезки длиной 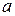 и и  соответственно. соответственно.

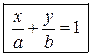 . (2.8) . (2.8)
Равенство (2.8) называется уравнением прямой в отрезках на осях.
Пример 2.1. Даны вершины  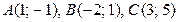 . Сделать рисунок. Найти: 1) уравнение стороны . Сделать рисунок. Найти: 1) уравнение стороны  ; ;
2) уравнение медианы  ; ;
3) уравнение высоты  ; ;
4) координаты точки пересечения медианы  и высоты и высоты  . .
Решение. 1) Воспользуемся уравнением (2.7):
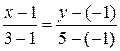 Þ Þ  Þ Þ  . .
Итак,  - уравнение стороны - уравнение стороны  . .
2) Находим координаты точки  - середины - середины  : :
 ; ;  . .
Следовательно,  . Используя формулу (2.7), находим уравнение медианы . Используя формулу (2.7), находим уравнение медианы  : :
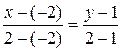 Þ Þ 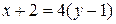 Þ Þ 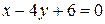 . .
Итак, 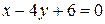 - уравнение медианы - уравнение медианы  . .
3) Рассмотрим вектор 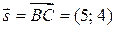 . Вектор . Вектор  , т.е , т.е  - нормальный вектор прямой - нормальный вектор прямой  . Чтобы составить уравнение высоты . Чтобы составить уравнение высоты  , воспользуемся формулой (2.1): , воспользуемся формулой (2.1):
 Þ Þ  . .
Итак,  - уравнение высоты - уравнение высоты  . .
4) Чтобы найти координаты точки  , где , где  , то составляем и решаем систему уравнений , то составляем и решаем систему уравнений
 Þ Þ  Þ Þ  . .
Итак,  - точка пересечения медианы - точка пересечения медианы  и высоты и высоты  . .
,
Пример 2.2. Найти угол наклона к оси  прямой L, если прямой L, если
 . .
Решение. Запишем уравнение прямой через угловой коэффициент:
 Þ Þ 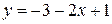 Þ Þ  . .
Значит,  . Следовательно, . Следовательно,  . , . ,
Расположение двух прямых на плоскости
Пусть заданы уравнения двух прямых  и и 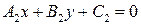 . Чтобы определить координаты точки пересечения составляют и решают систему уравнений: . Чтобы определить координаты точки пересечения составляют и решают систему уравнений:
 . .
Если система уравнений не имеет решений, то две прямые параллельны. Если система уравнений имеет бесчисленное множество решений, то две прямые совпадают.
Условия параллельности двух прямых
| Способы задания уравнений прямых
| Условия параллельности
| 1.  и и
 . .
 и и  - нормальные векторы - нормальные векторы
|  Û Û  Û Û 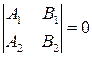 условия параллельности двух прямых, заданных общими уравнениями
условия параллельности двух прямых, заданных общими уравнениями
| 2. 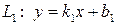 и и  . .
 и и  - угловые коэффициенты - угловые коэффициенты
|  Û Û 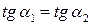 Û Û  условия параллельности двух прямых, заданных уравнениями с угловыми коэффициентами
условия параллельности двух прямых, заданных уравнениями с угловыми коэффициентами
| 3.  и и  . .
 и и  - направляющие векторы - направляющие векторы
|
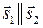 Û Û  Û Û  условия параллельности двух прямых, заданных канонически
условия параллельности двух прямых, заданных канонически
|
Условия перпендикулярности двух прямых
| Способы задания уравнений прямых
| Условия перпендикулярности
| 1.  и и
 . .
 и и  - нормальные векторы - нормальные векторы
|  Û Û  Û Û  условия перпендикулярности двух прямых, заданных общими уравнениями
условия перпендикулярности двух прямых, заданных общими уравнениями
| 2. 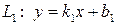 и и  . .
 и и  - угловые коэффициенты - угловые коэффициенты
|  Û Û 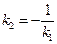 условия перпендикулярности двух прямых, заданных уравнениями с угловыми коэффициентами
условия перпендикулярности двух прямых, заданных уравнениями с угловыми коэффициентами
| 3.  и и 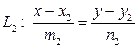 . .
 и и  - направляющие векторы - направляющие векторы
|
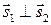 Û Û  Û Û  условия перпендикулярности двух прямых, заданных канонически
условия перпендикулярности двух прямых, заданных канонически
|
Угол между двумя прямыми
Под углом j между двумя прямыми  и и 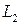 будем понимать наименьший угол, на который надо повернуть одну прямую, чтобы она стала параллельна другой прямой или совпала с ней. Ясно, что будем понимать наименьший угол, на который надо повернуть одну прямую, чтобы она стала параллельна другой прямой или совпала с ней. Ясно, что  , т.е. , т.е.  . .
Угол между двумя прямыми находится с учетом того, каким способом заданы уравнения прямых.
| Способы задания уравнений прямых
|
| 1.  и и
 . .
 и и  - нормальные векторы; - нормальные векторы; 
|  .
С условием того, что .
С условием того, что  , то выражение для , то выражение для  берется по абсолютной величине, т.е. берется по абсолютной величине, т.е.
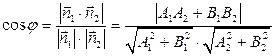 . .
| 2. 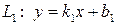 и и
 . .
 и и  - угловые коэффициенты - угловые коэффициенты
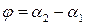
|  .
С условием того, что .
С условием того, что  , то выражение для , то выражение для  берется по абсолютной величине, т.е. берется по абсолютной величине, т.е.
 . .
| 3.  и и
 . .
 и и  - направляющие векторы - направляющие векторы

|  .
С условием того, что .
С условием того, что  , то выражение для , то выражение для  берется по абсолютной величине, т.е. берется по абсолютной величине, т.е.
 . .
|
Не нашли, что искали? Воспользуйтесь поиском по сайту:
©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|



 (2.3)
(2.3) . Действительно, из (2.2) имеем
. Действительно, из (2.2) имеем  . Обозначив
. Обозначив 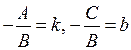 , придем к уравнению (2.3).
, придем к уравнению (2.3). прямой
прямой  .
.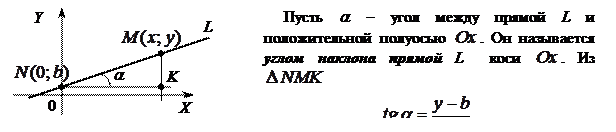
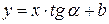 .
. и
и  . Сравнивая два уравнения, получаем
. Сравнивая два уравнения, получаем  .
. , т.е.
, т.е.  с угловым коэффициентом k.
с угловым коэффициентом k.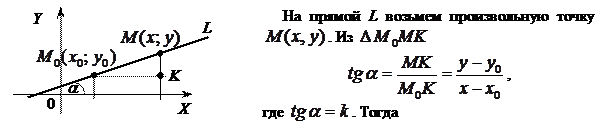
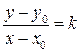 , или
, или . (2.4)
. (2.4) . Вектор
. Вектор  называется направляющим вектором прямой.
называется направляющим вектором прямой. . Найдем координаты вектора
. Найдем координаты вектора  :
:
 .
.
 . Тогда
. Тогда
 . (2.5)
. (2.5)
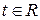 , что
, что  . Значит,
. Значит, , или
, или . (2.6)
. (2.6) и
и  .
.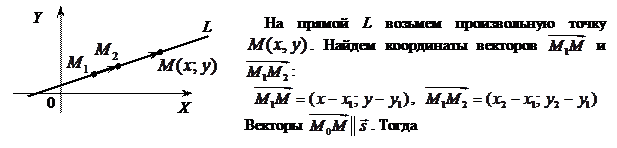
 . (2.7)
. (2.7) отсекает отрезки длиной
отсекает отрезки длиной 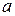 и
и  соответственно.
соответственно.
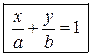 . (2.8)
. (2.8)
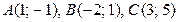 . Сделать рисунок. Найти: 1) уравнение стороны
. Сделать рисунок. Найти: 1) уравнение стороны  ;
; ;
; ;
;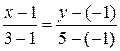 Þ
Þ  Þ
Þ  .
. - середины
- середины  ;
;  .
. . Используя формулу (2.7), находим уравнение медианы
. Используя формулу (2.7), находим уравнение медианы 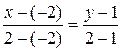 Þ
Þ 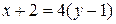 Þ
Þ 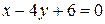 .
.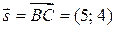 . Вектор
. Вектор  , т.е
, т.е  Þ
Þ  .
. , где
, где  , то составляем и решаем систему уравнений
, то составляем и решаем систему уравнений Þ
Þ  Þ
Þ  .
. - точка пересечения медианы
- точка пересечения медианы  .
. Þ
Þ 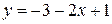 Þ
Þ  .
. . Следовательно,
. Следовательно,  . ,
. , и
и 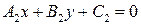 . Чтобы определить координаты точки пересечения составляют и решают систему уравнений:
. Чтобы определить координаты точки пересечения составляют и решают систему уравнений: .
. и
и
 .
.
 и
и  - нормальные векторы
- нормальные векторы
 Û
Û  Û
Û 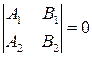 условия параллельности двух прямых, заданных общими уравнениями
условия параллельности двух прямых, заданных общими уравнениями
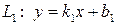 и
и  .
.
 и
и  - угловые коэффициенты
- угловые коэффициенты
 Û
Û 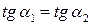 Û
Û  условия параллельности двух прямых, заданных уравнениями с угловыми коэффициентами
условия параллельности двух прямых, заданных уравнениями с угловыми коэффициентами
 и
и  .
.
 и
и  - направляющие векторы
- направляющие векторы
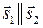 Û
Û  Û
Û  условия параллельности двух прямых, заданных канонически
условия параллельности двух прямых, заданных канонически
 Û
Û  Û
Û  условия перпендикулярности двух прямых, заданных общими уравнениями
условия перпендикулярности двух прямых, заданных общими уравнениями
 Û
Û 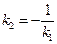 условия перпендикулярности двух прямых, заданных уравнениями с угловыми коэффициентами
условия перпендикулярности двух прямых, заданных уравнениями с угловыми коэффициентами
 и
и 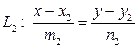 .
.
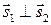 Û
Û  Û
Û  условия перпендикулярности двух прямых, заданных канонически
условия перпендикулярности двух прямых, заданных канонически
 и
и 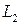 будем понимать наименьший угол, на который надо повернуть одну прямую, чтобы она стала параллельна другой прямой или совпала с ней. Ясно, что
будем понимать наименьший угол, на который надо повернуть одну прямую, чтобы она стала параллельна другой прямой или совпала с ней. Ясно, что  , т.е.
, т.е.  .
.
 .
С условием того, что
.
С условием того, что  берется по абсолютной величине, т.е.
берется по абсолютной величине, т.е.
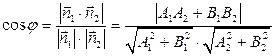 .
.
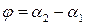
 .
С условием того, что
.
С условием того, что  .
.
 и
и
 .
.

 .
С условием того, что
.
С условием того, что  .
.