Как составляется уравнение движения груза в поперечном направлении при совместной работе механизмов подъема стрелы машин ТТ и груза?

Механизм подъема. Динамическое воздействие груза на кон­струкцию имеет место как при движении висящего на канатах груза, так и в процессе натягивания канатов, когда груз еще не оторвался от основания.

Рис. 8.6. Положения конца стрелы при перемещении

Рассмотрим упрощенную методику динамического расчета при подъеме груза. Результаты натурных тензометрических испытаний мостовых, портальных и других типов кранов дают возмож­ных. ib принять следующие допущения: усилия в канатах в про­цессе их натягивания, пока груз еще лежит на основании, воз­растают линейно, т. е, линейно возрастает нагрузка, приложенная к конструкции; после отрыва груза от основания, а также после торможения висящего на канатах груза, поскольку колебания второй частоты в конструкции малозаметны, а в канатах хотя и заметны, но быстро затухают, груз совместно с конструкцией совершает колебания той же частоты, т. е, канат по сравнению с конструкцией является весьма жестким.

Если "принять для динамического коэффициента значение по формуле (8.20), где в соответствии со сделанными допущениями:

; (8.25)

(где v — скорость подъема), то получим, что

где

(8.26)

Однако практически время Т оказывается то меньше, то больше, чем определенное по формуле (8.25), и более правиль­ным является определение величины по формуле

, (8.27)

где значения причем = 2, когда отрыв груза от основания производится с полной скоростью, что является наруше­нием условий эксплуатации и может рассматриваться лишь как особая нагрузка. Для отдельных групп кранов зна­чение устанавливается на основании дополнительных исследова­ний, зависящих от способа запуска подъемного механизма (не­регулируемый, регулируемый или автоматический). Если такие данные отсутствуют, то можно принимать для кранов общего наз­начения = 1,5. Чем больше грузоподъемность крана, тем меньше скорость подъема, избыточный момент двигателя (тормоза) и ча­стота его вращения, а потому и силы инерции при разго­нах (торможениях). При этом начинает проявляться демпфиру­ющее влияние потерь в полиспастной системе, которые в упро­щенной методике динамического расчета не учитываются, так как имеют для малых и средних грузоподъемностей при обычных для них скоростях небольшое значение.

Для предварительных расчетов значение динамического коэф­фициента конструкции можно также принимать равным значению его для каната при абсолютно жесткой конструкции, Тогда в соот­ветствии с решением дифференциальных .. уравнений движения конструкций при работе механизма подъема

(8.28)

Рассмотрим приближенное решение вопроса, когда перемещением массы у корня стрелы можно пренебречь и рас­сматривать упругую систему как имеющую одну степень свободы. При этом перемещение массы m_м на конце стрелы будет характе­ризоваться ее углом поворота.

Ускорение в вертикальной плоскости /_в = P/( _i + m_г). По­скольку перемещения б_г и 6_В достигаются в одно и то же время, ускорение в горизонтальной плоскости /',, = 6_г/„/6_м т. е.

(8.29)

Предполагается, что масса груза на гибком подвесе не оказы­вает влияния на значение Р_т, т. е. период поперечных- колебаний груза при наименьшей высоте его подвеса h (м)

(8.30)

значительно больше периода свободных колебаний конструкции как в вертикальной, так и в горизонтальной плоскости. В боль­шинстве практических случаев т₀ > Зт, что позволяет пренебречь влиянием второй частоты и пользоваться формулой (8.29).

Рассмотрим торможение опускающегося груаа. При упрощен­ном рассмотрении торможения опускающегося груза его можно принять мгновенным. Тогда вся кинетическая энергия груза V_H перейдет в потенциальную энергию каната U₁ и конструкции U_% и последняя будет испытывать наибольшую нагрузку. Так как

; ,

тогда ; U₂ = , а Р_д/f_д = , поэтому .

Тогда

и

Максимальное усилие

, (8.31)

т. е.

, (8.32)

где

. (8.ЗЗ)

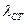Коэффициента, определенный по формуле (8.33), всегда меньше, чем определенный по формуле (8.26), если пред­ставляет собой только упругое удлинение каната (мостовые, козловые и другие краны, где канат, сходящий с барабана, висит вертикально). Это очевидно из энергетических соображений. При мгновенном торможении опускающегося груза его кинети­ческая энергия переходит в потенциальную энергию конструкции и канатов. При отрыве груза от основания в потенциальную энер­гию конструкции и канатов кроме кинетической энергии груза переходит еще кинетическая энергия массы конструкции, по­скольку к моменту отрыва груза от основания конструкция под влиянием натягивающихся канатов деформируется и масса ее обладает скоростью. Поэтому при упрощенном рассмотрении задачи (мгновенное торможение, пренебрежение затуханием ко­лебаний и т. п.), если скорости подъема и спуска одинаковы, дина­мический коэффициент при подъеме с основания больше, чем при торможении во время спуска. При двигателях постоянного тока при торможении опускающегося груза они будут оказывать тормозящее действие и снижать динамические нагрузки.

Не нашли, что искали? Воспользуйтесь поиском по сайту: