
|
|
Локальный экстремум функции двух переменных. Наибольшее и наименьшее значение функции в замкнутой области1. Найти экстремумы функции z=x2-xy+y2+9x-6y+20.
Решение.Данная функция существует при x
2. Найти экстремумы функции z = x3+ 4x +y2 при условии y = 2 – x. Решение.Данная функция существует при x Найдем экстремум этой функции. Для этого вычислим ее производную и приравняем к нулю. Получим z/ = 3x2 +2x, 3x2 +2x =0. Решением уравнения является х = 0 и х = - 2/3. Исследование знака производной и поведение функции на интервалах запишем в таблицу
Следовательно, при х=-2/3 функция имеет максимум, равный 112/27, а при х=0 имеет минимум z=0.
3. Найти наибольшее и наименьшее значения функции Решение. Вычислим частные производные данной функции, получим 1). Пусть х = 0, у 2). Пусть у = 0, х 3). Пусть у=-3-х, х Сравним значения функции в найденных точках и выберем из них наибольшее и наименьшее значения. Zнаиб = 6 достигается в точках (-3,0) и (0,-3). Zнаим = -1 достигается в точке (-1, -1).
4. Найти квадратичную зависимость (МНК) для следующих данных
Решение. Составим вспомогательную таблицу
получаем а = 0,02, b = -16,64, с = -6,67. Тогда искомое уравнение у =0,02 х2 -- 16,64 х - 6,67. Ответ. у = 0,02 х2 - 16,64 х - 6,67.
Задания для аудиторной работы
1. Исследовать на экстремум функции: а)z=xy2-xy-xy3, x>0, y>0, б) 2. Найти экстремум функции 3. Найти наибольшее и наименьшее значения функции z = х-2у+5, в прямоугольнике
4. Применяя метод наименьших квадратов, найти эмпирическую формулу для приближенного представления функции заданной таблицей
5. Зависимость между сроком эксплуатации автомобиля и мощностью двигателя представлена в следующей таблице
Найти эмпирическую формулу линейной зависимости.
Семинарское занятие 4.3. Двойные интегралы 1. Построить область интегрирования и изменить порядок интегрирования в интеграле
Решение. По пределам интегрирования построим область интегрирования D (рис. 11 а). Она ограничена снизу линией
а) б) Рис. 11
Линия у = а касается окружности в точке (а, а). Так как интегрируем сначала по х, то найдем х как функцию у из уравнений параболы и окружности. Получим
Вычислим интегралы по выделенным областям. Будем иметь
Взяв сумму интегралов, получим = 2. Область D ограничена линиями у = 2, у = х, у =5- х= 4. Расставить пределы интегрирования в повторном интеграле по этой области.
Рис. 12.
Решение.Построим данную область D (рис. 12). Область D1 ограничена сверху прямой у=х, снизу окружностью у = 5 - Тогда Если предстоит интегрировать сначала по у, а затем по х, то повторный интеграл запишется в виде
3. Вычислить
4. Вычислить Решение. Построим область D (рис. 14). Парабола у2 = 2с2х, симметричная относительно Ох, проходящая через точку (0, 0), с2х2 + у2 = 3с2 – эллипс, имеющий полуоси а =
Тогда
5. Вычислить площадь фигуры, ограниченной параболами у2 = 8 х + 16 и у2 = -2х + 6. Решение. Площадь фигуры вычисляется по формуле
Рис. 15.
= 6. Нарисовать тело, объем которого выражается двойным интегралом Решение.Исходя из пределов интегрирования, область D ограничена линиями х = 0, х = 1, у = 0, у = 1-х. Она является основанием искомого тела. Образующая, перпендикулярная плоскости Оху, передвигаясь вдоль границы области D, оставляет за собою след – цилиндрическую поверхность. Подынтегральная функция есть z = 1-x-y, геометрическое изображение которой представляется поверхностью, накрывающей сверху описанную цилиндрическую поверхность (рис. 16).
= 7. Найти объем тела, ограниченного цилиндром х2 +z2 = a2 и плоскостями у = 0, z = 0, у = х. Сделать рисунок. Решение. х2 +z2 = a2 – цилиндр с образующей, параллельной оси Оу, у = 0, z = 0 – координатные плоскости, у = х. – плоскость, проходящая через ось Оz и прямую у = х, принадлежащую координатной плоскости Оху (рис. 17)
Рис. 17. Задания для аудиторной работы
1. Построить область и изменить порядок интегрирования в интеграле 2. Вычислить 3. Вычислить 4. Вычислить 5. Вычислить 6. Вычислить
7. Вычислить площадь области D, ограниченной линиями, заданными уравнениями у = х и у = 4х – х2. 8. Вычислить объем тела, ограниченного поверхностями z = 1+x2+y2 и z = 5.
Контролирующий блок Тест 1. Область определения функции A. половина плоскости, расположенная над прямой B. вся плоскость Oxy, кроме точек прямой линии x = -у; C. все точки двух углов между биссектрисами x = ±у, заключающими внутри себя ось Ox; D. вся плоскость Oxy, кроме точек прямых x = 0 и у = 0; E. точки прямой x = -у.
2. Область определения функции A.
3. Найти уравнение линий уровня функции z = y(1+x)/(1-x). A. y =1+(C/x)2; B. D. y = x2(C+1); E.
4. Какая из линий является линией уровня функции z = y2-x для z = 1? A. D.
6. Чему равен предел A. Не существует, B. ∞, C. 0, D. 2, E. Ответ отличен от приведенных. 7. Вычислить предел A. Не существует, B. ∞, C. 0, D. 1, E. Ответ отличен от приведенных.
8. По определению частной производной функции z=f(x,y) по переменной х является … A. ∆хz= f(x+∆x, y)- f(x, y); B. z/x=
9. Найти z /x функции z =xy/(x+y). A. z /x= (xy/(x+y))2; B. z /x= y/(x+y); C. z /x= (2y/(x+y))2; D. z /x= (2x/(x+y))2; E. z /x= (y/(x+y))2.
10. Найти z /y функции z = lnxy. A. z /y=
11. Найти дифференциал функции z = x2y-y2x. A. (2xy-y2)dx; B. (x2-2xy)dy; C. (2xy-y2)dx+(x2-2xy)dy;
12. Найти полную производную функции z = y A. et/2(sin t + 2cos t)/2; B. 3e3t+1sin t; C. (2t+1)/(t2 + t);
13. Найти A. 1-exy, B. -exy, C. y, D. ex, E. –ex.
14. z = sinx tgy. A. cosx/cosy; B. cosx tgy; C. cosx/cos2y; D. sinx/cos2y;
15. Какая область является элементарной относительно оси Ox? 1) A. 1); B. 2); C. 3); D. Все; E. Нет среди предложенных.
16. Какое утверждение верное? § 1) Интегральная сумма § 2) Двойной интеграл функции z=f(x,y) на множестве D § 3) Если f(x,y)≡1 для всех (х,у)єD, то A. 1) и 2); B. 1) и 3); C. 2) и 3); D. Все; E. Нет верных.
17. Дописать утверждение: «Если функция z=f(x, y) непрерывна и неотрицательна в области D, то § 1) объем тела, образованного поверхностью z=f(x, y); § 2) объем прямого цилиндрического тела (цилиндра), построенного на области D как на основании и ограниченного сверху поверхностью z=f(x, y); § 3) площадь области D. A. 1); B 2); C. 3); D. 1), 2), 3); E. Нет правильных вариантов. 18. Повторный интеграл 1) A. 1); B. 2); C. 3); D. 1), 2), 3); E. Нет правильных вариантов.
А.
20. Изменить порядок интегрирования в повторном интеграле А.
21. Вычислить двойной интеграл А. 4, B. 0, C. 1, D. Не существует, E. Ответ отличен от приведенных
22. Градиентом функции z = ln(x+y2) в точке М (1, 2) является grad z =… A. {1/5,1/5}; B. {4/5,4/5}; C. {1/5,4/5}; D. {1,4/5}; E. {1/5,5}
23. Найти градиент функции z = yx в точке М(х, у). A. {y lny, xyx-1}; B. {yx lny, yx-1}; C. {yx lny, xyx};
24. Найти экстремумы функции z = x2 + xy + y2- 6x - 9y. A. Экстремумов нет; B. Zmin(1, 4) = -21; C. Zmax(0, 0) = 0; D. ∆ = 0, требуется доп. исследование; E. Zmax(-1, 0) = 7.
25. Какая из предложенных систем в методе наименьших квадратов (МНК) определяет коэффициенты линейной функции у=ах + в, аппроксимирующей заданную таблично функцию? 1) 3) A. 1), B. 2), C. 3), D. Все, E. Нет среди предложенных.
26. Что означают частные эластичности производственной функции Кобба-Дугласа z=b0xb1yb2? Варианты ответов: § 1) Ех(z) = b1, Ey(z) = b2 приближенно показывают на сколько процентов изменится выпуск продукции при изменении только затрат труда x или только объема производственных фондов y на 1%; § 2) Ех(z) = b1, Ey(z) = b2 приближенно показывают на сколько изменится выпуск продукции при изменении только затрат труда x или только объема производственных фондов y на 1 ед.; § 3) Ех(z) = b0b1, Ey(z) = b0b2 приближенно показывают на сколько процентов изменится выпуск продукции при изменении только затрат труда x или только объема производственных фондов y на 1%. A. Ответ отличен от приведенных утверждений, B. Неверными являются 1) и 2), C. Неверными являются 2) и 3), D. Неверными являются 1) и 3), E. Все.
27. Вычислить приближенное значение 3,012,03, исходя из значения функции Z= xy при х = 3, у = 2, заменяя ее приращение дифференциалом. A. 9; B. 0,36; C. 9,06; D. 9,36; E. 9,3
28. Применяя двойной интеграл, найти площадь фигуры, ограниченной линиями: у = х, у = 1/х, у = 0, х = е. A. B. C. D. E.
29. Найти наибольшее и наименьшее значения функции z=xy2 при х2+у2≤ 3. A. Нет наибольшего и наименьшего значений данной функции при указанном ограничении; B. Наибольшее и наименьшее значения данной функции достигаются в экстремальных точках, лежащих на прямой у=0 при хε[- C. Zнаим= -2 в точках (-1;± D. Невозможно определить наибольшее и наименьшее значения функции, т.к. Δ=0, необходимы дополнительные исследования; E. Ответ отличен от приведенных.
30. По какой формуле можно вычислить объем тела, ограниченного поверхностью Z=4-x2- y2 и плоскостью Oxy? A. V = πr2H, где r = 2, H = Z(x, y); B. C. D. E. Ответ отличен от приведенных.
Литература 1. Ведина О. И., Десницкая В. Н., Варфоломеева Г. Б., Тарасюк А. Ф. Математика. Математический анализ для экономистов. Учебник / Под ред. А. А. Гриба и А. Ф. Тарасюка – М.: Информационно-издательский дом «Филинч», Рилант, 2006. 2. Ермаков В. И. и др. Общий курс высшей математики для экономистов. Учебник / Под ред. В. И. Ермакова – М.: ИНФРА – М, 2001. 3. Ермаков В. И. и др. Сборник задач по высшей математике для экономистов. Учебник / Под ред. В. И. Ермакова – М.: ИНФРА – М, 2001. 4. Красс М. С., Чупрынов Б. П. Основы математики и ее приложения в экономическом образовании. Учеб. – 2-е издание испр. – М.: Дело, 2001. 5. Кремер Н.Ш. и др. Высшая математика для экономистов / Под ред. Н. Ш. Кремера, – М.: ЮНИТИ, 2005. 6. Кремер Н.Ш. и др. Практикум по высшей математике для экономистов / Под ред. Н. Ш. Кремера, – М.: ЮНИТИ, 2005. 7. Кузнецов А. В. и др. Сборник задач и упражнений по высшей математике: Общий курс: Учебное пособие / А.В. Кузнецов, Д. С. Кузнецов, Е. И. Шилкина и др. – Мн.: Высшая школа, 2001. 8. Миселимян Т. Л. Тренировочные тесты по математике. Ч 1, 2. Уч.-мет. пособ.– Кр-р. 2006. 9. Миселимян Т. Л., Бабаянц Ю. В. Основы высшей математики. Функции нескольких переменных. Уч. пособ. для студентов экономических специальностей. – Кр-р. 2007. 10. Солодовников А. С., Бабайцев В. А., Бранков А. В., Шандра И.Г. Математика в экономике.Учеб. – 2-е издание перераб. и доп., Ч.1– М.: Финансы и статистика, 2006. 11. Солодовников А. С., Бабайцев В. А., Бранков А. В., Шандра И.Г. Математика в экономике.Учеб. – 2-е издание перераб. и доп., Ч.2– М.: Финансы и статистика, 2005. 12. Шипачев В.С. Высшая математика. Учеб. – 7-е издание, стер. – М.: Высшая школа, 2005. Учебное издание

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 R и y
R и y  , найдем критическую точку М(-4,1). Вычислим вторые частные производные
, найдем критическую точку М(-4,1). Вычислим вторые частные производные  =2 (обозначим А),
=2 (обозначим А),  =2 (обозначим С),
=2 (обозначим С),  =-1(обозначим В). Тогда дискриминант равен АС-В2 = 2*2-1=3 > 0. Следовательно, есть экстремум, и так как А = 2, то функция имеет минимум z (- 4, 1) = -1. Ответ. Минимум z (- 4, 1) = -1.
=-1(обозначим В). Тогда дискриминант равен АС-В2 = 2*2-1=3 > 0. Следовательно, есть экстремум, и так как А = 2, то функция имеет минимум z (- 4, 1) = -1. Ответ. Минимум z (- 4, 1) = -1. в области, ограниченной линиями х =0, у =0, х+у =-3.
в области, ограниченной линиями х =0, у =0, х+у =-3.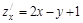 ,
,  . Приравниваем их к нулю и решаем систему уравнений
. Приравниваем их к нулю и решаем систему уравнений  и
и  . Получим критическую точку М1(-1,-1), и значение функции в ней будет равно z(М1) = -1. Исследовать ее на экстремум не следует, так как, если функция имеет наибольшее или наименьшее значения, то они достигаются либо в критических точках, принадлежащих указанной области, либо на границе области. Поэтому далее мы будем исследовать функцию на границе области.
. Получим критическую точку М1(-1,-1), и значение функции в ней будет равно z(М1) = -1. Исследовать ее на экстремум не следует, так как, если функция имеет наибольшее или наименьшее значения, то они достигаются либо в критических точках, принадлежащих указанной области, либо на границе области. Поэтому далее мы будем исследовать функцию на границе области.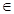 [-3, 0]. Тогда
[-3, 0]. Тогда  . Требуется найти критические точки функции z на выбранной границе, а также вычислить ее значение на концах отрезка. Для этого вычислим ее производную, приравняем к нулю, получим
. Требуется найти критические точки функции z на выбранной границе, а также вычислить ее значение на концах отрезка. Для этого вычислим ее производную, приравняем к нулю, получим  ,
,  или
или  . Таким образом, критическая точка на границе М2(0,-1/2) и z (М2) = -1/4. Вычислим значения функции на концах отрезка z (0, 0) = 0, z (0,-3) = 6.
. Таким образом, критическая точка на границе М2(0,-1/2) и z (М2) = -1/4. Вычислим значения функции на концах отрезка z (0, 0) = 0, z (0,-3) = 6. . Проводим исследование, аналогичное предыдущему. Получим критическую точку М3 (-1/2, 0) и z (М3) = -1/4. Вычисляем значение функции на одном конце отрезка, так как на другом уже вычислили, получим z (-3, 0) = 6.
. Проводим исследование, аналогичное предыдущему. Получим критическую точку М3 (-1/2, 0) и z (М3) = -1/4. Вычисляем значение функции на одном конце отрезка, так как на другом уже вычислили, получим z (-3, 0) = 6. ,
,  и М4(-3/2, -3/2) – критическая точка. Значение функции в этой точке равно
и М4(-3/2, -3/2) – критическая точка. Значение функции в этой точке равно 
 Параметры определяем из системы
Параметры определяем из системы ,
,
 при условии, что
при условии, что  .
. ,
,  , х+у≤1.
, х+у≤1. .
. , сверху линией
, сверху линией  , а справа и слева соответственно х = 0, х = 2а. Линия
, а справа и слева соответственно х = 0, х = 2а. Линия 

 и
и  .
. ,
,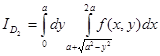 ,
,  .
. =
=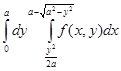 +
+  +
+ 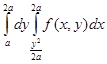 .
. , х= 0,
, х= 0,
 , центр которой в точке (0, 5), R=5. Область D2 ограничена сверху прямой у = 2, а снизу той же окружностью. Если предстоит интегрировать сначала по х, а затем по у,то область D1 и D2 можно объединить в одну область D. Найдем х как функцию у из уравнения окружности
, центр которой в точке (0, 5), R=5. Область D2 ограничена сверху прямой у = 2, а снизу той же окружностью. Если предстоит интегрировать сначала по х, а затем по у,то область D1 и D2 можно объединить в одну область D. Найдем х как функцию у из уравнения окружности  . Для данной области надо брать со знаком «+», то есть
. Для данной области надо брать со знаком «+», то есть  или
или  .
.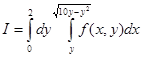 .
. +
+  .
. , где область D ограничена линиями, заданными уравнениями у=1/х, у = х и х = 2.
, где область D ограничена линиями, заданными уравнениями у=1/х, у = х и х = 2.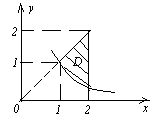 Рис. 13.
Рис. 13.
 .
Интегрируем внутренний интеграл при фиксированном (постоянном) х, находим
.
Интегрируем внутренний интеграл при фиксированном (постоянном) х, находим

 =
=  =9/4.
=9/4. , где область D ограничена линиями, заданными уравнениями у2 = 2с2х, с2х2 + у2 = 3с2, у ≥ 0, с > 0.
, где область D ограничена линиями, заданными уравнениями у2 = 2с2х, с2х2 + у2 = 3с2, у ≥ 0, с > 0. и b = c
и b = c 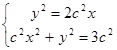 . Введем обозначение у2 = z, тогда
. Введем обозначение у2 = z, тогда Рис. 14.
Рис. 14.
 или
или  .
Корни этого уравнения есть
.
Корни этого уравнения есть  ,
,  . И так как
. И так как 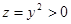 , то выбираем только
, то выбираем только  или
или  . Ему соответствует значение х = 1.
. Ему соответствует значение х = 1.
 =
=  = =
= =  =
= 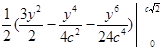 =
=  .
. , где D – область, ограниченная параболами (рис. 15). Параболы пересекаются в точках (-1,-2
, где D – область, ограниченная параболами (рис. 15). Параболы пересекаются в точках (-1,-2  ), (-1, 2
), (-1, 2 
 =
=  =
= =
= 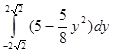 = =
= =  = 5 (2
= 5 (2  (16
(16  (кв. ед.).
(кв. ед.). . Найти объем этого тела.
. Найти объем этого тела. Рис. 16.
Рис. 16.

 =
=
=
=  =
=
 =
=  =
=  =1/6 (куб. ед.).
=1/6 (куб. ед.). =
=  = =
= =  =
=  =
=  .
.
 .
. , где область D ограничена линиями у=2-х2, у = х, у = 6-х2.
, где область D ограничена линиями у=2-х2, у = х, у = 6-х2. , где область D ограничена линиями у=х, у =2х, у = -х+4.
, где область D ограничена линиями у=х, у =2х, у = -х+4. , где область D ограничена линиями у=ех, у =е2х , х=2.
, где область D ограничена линиями у=ех, у =е2х , х=2. , где область D ограничена линиями ху=1, у=0, х=2, х=3.
, где область D ограничена линиями ху=1, у=0, х=2, х=3. , где область D ограничена линиями у=х2, х=2, у = 4х2.
, где область D ограничена линиями у=х2, х=2, у = 4х2. есть…
есть… изображена на рисунке …
изображена на рисунке … B.
B.  C.
C.  D.
D.  E.
E. 
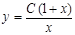 ; C.
; C.  ;
; .
. ; B.
; B.  ; C.
; C.  ;
; ; E.
; E.  .
.
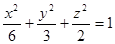 ;
B.
;
B.  ;
C. x + y + z = 6;
D.
;
C. x + y + z = 6;
D.  ;
E. z = x2 + y2.
;
E. z = x2 + y2.
 ?
? .
. ; С. z/x=
; С. z/x=  ;
; 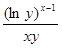 ; B. z /y=
; B. z /y=  ; C. z /y=
; C. z /y=  ;
;  ; E. z /y= 1/xy.
; E. z /y= 1/xy. , где x = et, y = sin t.
, где x = et, y = sin t. , если z=х-еху.
, если z=х-еху. =…
=… 2)
2)  3)
3) 
 функции z=f(x,y) на множестве D не зависит от способа разбиения множества D на элементарные ячейки и от выбора точек
функции z=f(x,y) на множестве D не зависит от способа разбиения множества D на элементарные ячейки и от выбора точек  в каждой ячейке;
в каждой ячейке; не зависит от способа разбиения множества D на элементарные ячейки и от выбора точек
не зависит от способа разбиения множества D на элементарные ячейки и от выбора точек  численно равен площади области D.
численно равен площади области D. вычисляется по области D:
вычисляется по области D: 2)
2)  3)
3) 

 ; B.
; B.  ; C.
; C.  ;
;  ; E.
; E.  .
. .
. ; B.
; B. 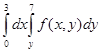 ; C.
; C.  ;
;  ; E.
; E.  , где D – область, ограниченная линиями х= 1, у = 4 и осями координат.
, где D – область, ограниченная линиями х= 1, у = 4 и осями координат. ; 2)
; 2)  ;
;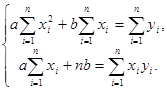
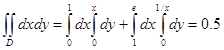 ;
; ;
; ;
; ;
; .
.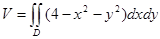 , где D область ограниченная линией x2 + y2=4;
, где D область ограниченная линией x2 + y2=4; ;
; ;
;