
|
|
Лекция 4.3 «Функции нескольких переменных »Вопросы: 1.Понятие двойного интеграла Пусть функция
Рис 3.
Площадь части области D, покрытая неполными клетками, уменьшается при увеличении числа клеток разбиения, то есть при уменьшении размеров клеток. Пронумеруем клетки индексами i (i = 1,2,…,n) по горизонтали и j (j = 1,2,…,m) по вертикали (считая слева направо и снизу вверх). Клетка ∆ij будет иметь длину ∆хi по горизонтали и ∆yj по вертикали и площадь, равную ∆хi∆yj, которая будет стремиться к нулю при ∆хi→0 и ∆yj→0. В каждой элементарной части возьмем произвольную точку (ξi ;ηj) и составим выражение Таким образом, по определению
Если
Свойства двойного интеграла: 1. Если 2. Если 3. Пусть область D является объединением областей D1 и D2. Если функция 4. Пусть 5. Пусть даны две функции 6. Пусть Интегралы вида
называются повторными (или двукратными) и обычно записываются так I1= каждый из которых есть результат последовательного вычисления двух обыкновенных определенных интегралов. Как правило, пределы при первом интегрировании являются переменными, зависят от той переменной, которая при этом рассматривается как постоянная. Пределы при втором интегрировании всегда постоянны. Геометрически эти пределы изображаются линиями, ограничивающими область D. В первом случае повторного интеграла это линии х = а, х = b, Область D в этом случае такова, что всякая прямая, параллельная оси Оу и проходящая через внутреннюю точку (точка не лежащая на границе области), пересекает границу области в двух точках N1 и N2. Такую область мы будем называть правильной в направлении оси Оу. Заметим, что вход в нее и выход осуществляется только одним способом, пересекая линии у = у1(х) и у = у2(х) (рис. 5). Во втором случае повторного интеграла область D ограничена линиями у = с и у = d, х = х1(у) и х = х2(у) (предположим, что эти функции непрерывны на [c, d]). Область D такова, что всякая прямая, параллельная оси Ох и проходящая через внутреннюю точку области, пересекает границу области в двух точках М1 и М2. Такую область называем правильной в направлении оси Ох (рис. 6).
Аналогично, как и в случае правильной области в направлении оси Оу, вход в эту область и выход осуществляется только одним способом, то есть пересекая линии х = х1(у) и х = х2(у). Область, правильную как в направлении оси Оу, так и в направлении оси Ох, мы будем называть просто правильной областью D. Например, область D, ограниченная прямыми х = а, х = b, у = с, у = d, является правильной, так как все требования, указанные выше, выполняются.
ID=ID1+ID2. (15) Теорема. Двойной интеграл от непрерывной функции
Практические занятия Семинарское занятие 4.1. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 определена и ограничена в замкнутой области
определена и ограничена в замкнутой области  . Разобьем эту область эту область на N элементарных частей D1, D2, …, DN, таких, что
. Разобьем эту область эту область на N элементарных частей D1, D2, …, DN, таких, что 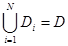 . Для упрощения рассуждений это разбиение проведем прямыми, параллельными осям координат Ox и Oy (рис. 3) и будем считать область D выпуклой и все полные клетки имеют одинаковые размеры.
. Для упрощения рассуждений это разбиение проведем прямыми, параллельными осям координат Ox и Oy (рис. 3) и будем считать область D выпуклой и все полные клетки имеют одинаковые размеры.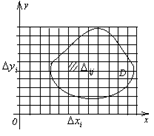
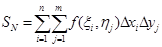 , которое называется интегральной суммой функции двух переменных. Обозначим через d – диаметр клетки, то есть наибольший линейный размер ее (в данном случае
, которое называется интегральной суммой функции двух переменных. Обозначим через d – диаметр клетки, то есть наибольший линейный размер ее (в данном случае  – длина диагонали клетки). Вычислим предел Sn при N→∞ (n→∞ и m→∞) и d→0. Если он существует и не зависит от способа разбиения области D на элементарные площадки и выбора точек (ξi ;ηj), то функция
– длина диагонали клетки). Вычислим предел Sn при N→∞ (n→∞ и m→∞) и d→0. Если он существует и не зависит от способа разбиения области D на элементарные площадки и выбора точек (ξi ;ηj), то функция 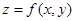 называется интегрируемой на множестве D, а само значение предела называется двойным интегралом функции
называется интегрируемой на множестве D, а само значение предела называется двойным интегралом функции  .
.
 .
.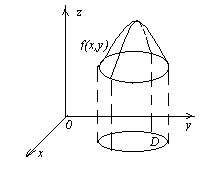 Рис. 4
Рис. 4
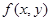 =1 для всех x, y из D, то
=1 для всех x, y из D, то 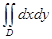 численно равен площади области D.
численно равен площади области D.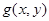 интегрируемы в области D, то
интегрируемы в области D, то  (
( 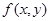 ±
± 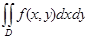 ±
± 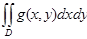 .
.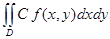 = С
= С  +
+  .
. (х, у)
(х, у) 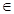 D, то
D, то  .
. ≤
≤ 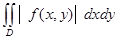 .
.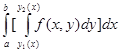 и
и 
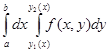 , I2=
, I2= 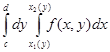 ,
,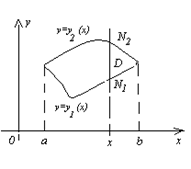 Рис. 5
Рис. 5
 Рис.6
Рис.6
 Рис. 7.
Рис. 7.
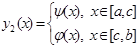 Тогда область D разобьем на две правильные области D1 и D2 в направлении оси Оу. (рис.7). Повторный интеграл ID по области D будет равен сумме таких же интегралов по областям D1 и D2, то есть
Тогда область D разобьем на две правильные области D1 и D2 в направлении оси Оу. (рис.7). Повторный интеграл ID по области D будет равен сумме таких же интегралов по областям D1 и D2, то есть