
|
|
Лекция 4.1 «Функции нескольких переменных»МАТЕМАТИЧЕСКИЙ АНАЛИЗ ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ Учебно-методическое пособие
Краснодар
УДК 517 ББК 22.12 С13
В учебно-методическом пособии использованы материалы, разработанные доцентом кафедры «Информатика и ЭММ» Миселимян Т.Л.
Рецензенты: Доктор технических наук, профессор факультета педагогики, психологии и коммуникативистики КубГУ, г. Краснодар, Ю.И. Дударев
Кандидат педагогических наук, профессор кафедры «Информатика и ЭММ» Южного института менеджмента, г. Краснодар, Б.А. Бурняшов Савчук С.Б. С13 Функции нескольких переменных. Учебно-методическое пособие. –Краснодар: ЮИМ, 2012. –47с.
В учебно-методическом пособии разработаны обучающий и контролирующий блоки, содержащие материал, соответствующий содержанию 4-го раздела «Функции нескольких переменных» учебной дисциплины «Математический анализ». Предложены тезисы-лекции, решения типовых упражнений, задания для самостоятельной работы студентов, а также варианты тестов. Пособие предназначено для подготовки студентов направлений 080100 Экономика, 080200 Менеджмент,100400 Туризм. Оно также может быть использовано преподавателями «Математического анализа» и «Математики» в учебном процессе при систематизации учебного материала и для контроля уровня усвоения данной темы. Рекомендовано к изданию научно-методическим советом
Ó Издательство ЮИМ Содержание
Пояснительная записка. 4 Обучающий блок. 5 Содержание лекций (тезисы) 5 Практические занятия. 19 Контролирующий блок. 39 Литература. 46
Пояснительная записка.
Структура учебно-методического пособия содержит обучающий блок и контролирующий блок. В обучающем блоке структурирован учебный материал по нескольким ведущим темам раздела «Функции нескольких переменных». Это позволяет систематизировать большой объем учебного материала в единую логически связанную систему. Каждая тема разбита на отдельные вопросы, определенная порция которых изучается, как правило, в течение одной лекции. Материал этого блока представлен в форме тезисов. Для выработки навыков на практических (семинарских) занятиях предлагаются решения типовых упражнений. Контролирующий блок состоит из контрольного тестирования. Разработанные блоки носят как учебно-методический, так и чисто практический характер. Не претендуя на полноту и окончательность теоретического и практического содержания раздела, пособие, по мнению авторов, должно способствовать более четкому и содержательному представлению курса Математического анализа, повысить качество формирования у студентов общекультурных и профессиональных компетенций, системы математических знаний и умений, являющихся составными компонентами экономических знаний и умений, а также способствовать повышению методической компетентности преподавателей.
Обучающий блок
Содержание лекций (тезисы) Лекция 4.1 «Функции нескольких переменных» Вопросы: 1.Евклидово пространство Еm. 2.Множество точек Евклидова пространства. 3.Понятие функции. 4.Линии уровня, частные производные. 5.Полный дифференциал. 6.Производная по направлению. Координатное пространство 1) 2) 3) 4)
Определение. Множество точек Если Определение.Пусть даны Определение. Если любая выколотая Определение. Множество Определение.Будем говорить, что в области
Множество Обозначения в случае
Основные способы задания функции f(M) – аналитический, геометрический и табличный. Функции нескольких переменных Функции нескольких переменных заданы параметрически, если n аргументов и функция выражены явно через n новых переменных (параметров):
(для случая двух переменных). Аналогично для случая Кривые, получающиеся в сечении поверхности и спроектированные на плоскость Oxy, называют линиями уровня. Их уравнение Пусть функция f(M) определена на множестве
Определение. Число А называется пределом функции Определение.Говорят, что функция f (M) имеет предел, равный бесконечности при М→М0, если для любого N > 0 найдется выколотая Определение.Функция Аналогично случаю функции одной переменой для пределов функций Определение.Если
Теорема.Сумма и произведение конечного числа функций бесконечно малых в точке M0, а также произведение бесконечно малой в точке M0 на ограниченную функцию являются функциями бесконечно малыми в точке M0. Определение.Пусть функция Теорема. Всякая элементарная функция нескольких переменных непрерывна в каждой точке своей области определения. Определение.Функция n переменных называется непрерывной на множестве Теорема.Всякая функция, непрерывная на замкнутом ограниченном множестве, принимает на нем наибольшее и наименьшее значения. Теорема. Если непрерывная в точке функция принимает в этой точке положительное (или отрицательные) значения, то она принимает значения того же знака во всех точках достаточно близких к данной. Если в некоторой точке 1) функция 2) функция 3) функция Пусть дана поверхность Частным приращением z по x обозначают
Частное приращение z по y.
Определение.Частной производной функции нескольких переменных по одной из этих переменных называется предел (если он существует) отношения соответствующего частного приращения функции к приращению рассматриваемой независимой переменной при стремлении последнего к нулю, то есть
Самое вычисление частной производной осуществляется по правилам дифференцирования функции одной переменной, при этом все независимые переменные, кроме одной, по которой вычисляется частная производная, считаются Сообщив аргументу х приращение
Замечание. Теорема. Если частные производные
где Определение. Функция
где A и B– числа,
Теорема.Если функция
Определение. При выполнении соотношения (5.11) функция
Если
если Тогда дифференциал функции можно записать через дифференциалы независимых переменных
Выражение Следовательно, компактная запись выражения (9),
Теорема. Пусть даны функция
Теперь рассмотрим тот случай, когда функции x и у зависят не от одной переменной t. Например,
аналогично по переменной v Если функция z=f(x,y) имеет в точке М(х,у) непрерывные частные производные, то в этой точке существует и производная по любому направлению, исходящему из точки М(х,у); вычисляется эта производная по формуле где 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 (или n-мерное векторное пространство) будет Евклидовым n-мерным пространством
(или n-мерное векторное пространство) будет Евклидовым n-мерным пространством 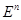 , если в нем определено скалярное произведение двух n-мерных векторов, удовлетворяющее свойствам:
, если в нем определено скалярное произведение двух n-мерных векторов, удовлетворяющее свойствам: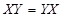 ;
;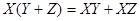 ;
;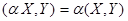 ;
;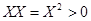 , если
, если 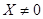 , то есть, указан способ определения расстояния между двумя точками
, то есть, указан способ определения расстояния между двумя точками 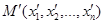 и
и 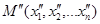
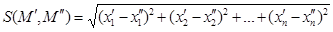 .
.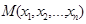 принадлежащих Rn и удовлетворяющих неравенству
принадлежащих Rn и удовлетворяющих неравенству 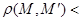
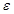 , называется
, называется 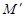 и обозначается Оε(
и обозначается Оε( 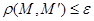 , то n-мерный шар называется замкнутым; если
, то n-мерный шар называется замкнутым; если 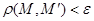 , то n-мерный шар называется открытым. При
, то n-мерный шар называется открытым. При 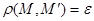 , будем иметь n-мерную сферу радиуса
, будем иметь n-мерную сферу радиуса 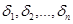 n положительных чисел и точка
n положительных чисел и точка 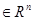 . n-мерным
. n-мерным  параллелепипедом с центром в точке
параллелепипедом с центром в точке 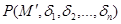 , координаты точек которого удовлетворяют условию
, координаты точек которого удовлетворяют условию 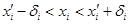 ,
, 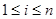 . Двумерный параллелепипед называется прямоугольником.
. Двумерный параллелепипед называется прямоугольником.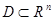 , то
, то 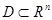 называется ограниченным, если существует n-мерный параллелепипед
называется ограниченным, если существует n-мерный параллелепипед 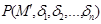 , содержащий множество D.
, содержащий множество D.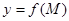 или
или 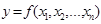 , если для любой точки
, если для любой точки 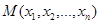 из области D по какому-либо закону ставится в соответствие некоторое число
из области D по какому-либо закону ставится в соответствие некоторое число 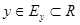 , обозначаемое
, обозначаемое 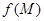 и называемое значением функции в точке М.
и называемое значением функции в точке М.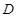 называется областью определения функции, а Е – областью изменения функции
называется областью определения функции, а Е – областью изменения функции 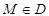 может быть любой, то ее компоненты можно рассматривать как переменные величины. Компоненты
может быть любой, то ее компоненты можно рассматривать как переменные величины. Компоненты 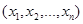 точки М называют независимыми переменными или системой значений аргументов, а
точки М называют независимыми переменными или системой значений аргументов, а 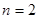 ,
, 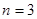 : функция двух переменных
: функция двух переменных 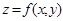 ; функция трех переменных
; функция трех переменных 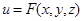 .
.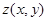 заданы неявно, когда аргументы и функция связаны уравнением
заданы неявно, когда аргументы и функция связаны уравнением 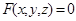 .
.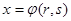 ,
,  ,
, 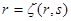
 .
.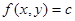 .
. , и точка M0 является предельной точкой множества
, и точка M0 является предельной точкой множества 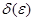 -окрестность точки М0, такая, что
-окрестность точки М0, такая, что 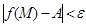 для всех
для всех 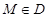 ,
, 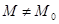 и
и 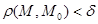 . Обозначается предел так
. Обозначается предел так 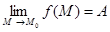 .
.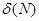 -окрестность точки M0, такая, что │f (M)│>N для всех M
-окрестность точки M0, такая, что │f (M)│>N для всех M 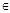 D, М≠М0,
D, М≠М0, 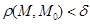 . Обозначение
. Обозначение 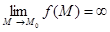 .
.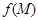 называется ограниченной на множестве D, если существует такое число K, что
называется ограниченной на множестве D, если существует такое число K, что  для всех
для всех 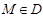 .
.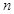 переменных справедливы соответствующие теоремы о пределах суммы, произведения и частного.
переменных справедливы соответствующие теоремы о пределах суммы, произведения и частного.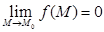 , то функция
, то функция 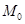 .
.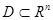 , M0 – предельная точка D. Функция называется непрерывной в точке M0, если существует предел функции в точке M0, равный значению функции в этой точке, то есть
, M0 – предельная точка D. Функция называется непрерывной в точке M0, если существует предел функции в точке M0, равный значению функции в этой точке, то есть 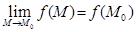 .
.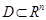 , если она непрерывна в каждой точке этого множества.
, если она непрерывна в каждой точке этого множества.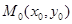 не выполняется условие непрерывности функции
не выполняется условие непрерывности функции 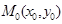 , за исключением самой точки
, за исключением самой точки 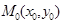 ;
;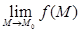 ;
;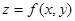 .
.
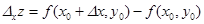 (1)
(1)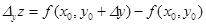 (2)
(2)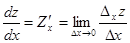 (3)
(3)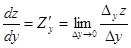 (4)
(4)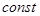 .
. , а аргументу у – приращение
, а аргументу у – приращение 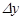 , получим для
, получим для 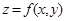 новое приращение
новое приращение 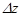 , которое называется полным и определяется по формуле
, которое называется полным и определяется по формуле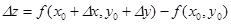 (5)
(5)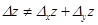 .
.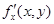 ,
, 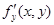 существуют в точке
существуют в точке 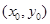 и в некоторой ее окрестности, а также являются непрерывными функциями аргументов
и в некоторой ее окрестности, а также являются непрерывными функциями аргументов 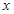 ,
,  в этой точке, то имеет место формула
в этой точке, то имеет место формула (6)
(6)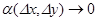 ,
, 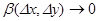 при
при 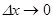 ,
,  .
.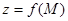 , определенная на множестве D и непрерывная в точке M0, называется дифференцируемой в точке M0, если полное приращение в некоторой окрестности точки M0, можно представить в виде
, определенная на множестве D и непрерывная в точке M0, называется дифференцируемой в точке M0, если полное приращение в некоторой окрестности точки M0, можно представить в виде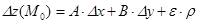 , (7)
, (7)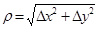 ,
, 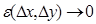 при
при 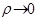 .
.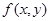 дифференцируема в точке
дифференцируема в точке 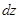 , то есть
, то есть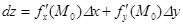 . (8)
. (8)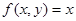 , то выражение (8) запишется в виде
, то выражение (8) запишется в виде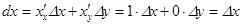 ,
,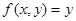 , то
, то 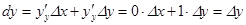 .
.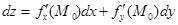 . (9)
. (9)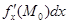 называется частным дифференциалом по х и обозначается символом dx z, то есть
называется частным дифференциалом по х и обозначается символом dx z, то есть 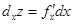 . Аналогично частным дифференциалом функции
. Аналогично частным дифференциалом функции 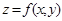 по у будет выражение
по у будет выражение 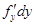 , то есть
, то есть 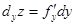 .
.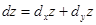 . (10)
. (10)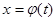 ,
, 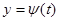 , определенные на множестве A. При этом
, определенные на множестве A. При этом 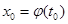 ,
,  , если
, если  ,
, 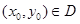 , то есть при изменении
, то есть при изменении  точки
точки 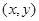 не выходят за пределы области D; и
не выходят за пределы области D; и 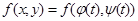 . Если функция
. Если функция 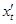 и
и  в соответствующей точке t0, то сложная функция
в соответствующей точке t0, то сложная функция 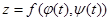 также имеет производную в точке
также имеет производную в точке 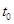 , равную
, равную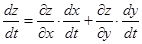 . (11)
. (11)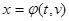 ,
, 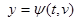 . Кроме существования и непрерывности частных производных функции z=f(x,y) в точке (x0-,y0), мы предполагаем здесь существование и непрерывность частных производных от функций x и y по переменным t и v в соответствующей точке (t0,v0). После подстановки функций φ и ψ в функцию f мы будем иметь функцию от двух переменных t и v. Возникает вопрос о существовании частных производных
. Кроме существования и непрерывности частных производных функции z=f(x,y) в точке (x0-,y0), мы предполагаем здесь существование и непрерывность частных производных от функций x и y по переменным t и v в соответствующей точке (t0,v0). После подстановки функций φ и ψ в функцию f мы будем иметь функцию от двух переменных t и v. Возникает вопрос о существовании частных производных  и
и 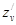 . Этот случай отличается от уже изученного тем, что вместо полной производной функции z мы будем иметь частные производные по переменным t и v, и вместо производных функции одной переменной
. Этот случай отличается от уже изученного тем, что вместо полной производной функции z мы будем иметь частные производные по переменным t и v, и вместо производных функции одной переменной 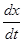 и
и 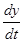 будут частные производные
будут частные производные 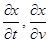 и
и 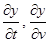 . Поэтому формула (11) имеет вид
. Поэтому формула (11) имеет вид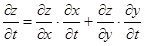 , (12)
, (12) .
.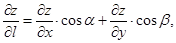
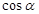 и
и 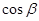 напраляющие косинусы вектора l0, где
напраляющие косинусы вектора l0, где  .
.