
|
|
Некоторые виды функций нескольких переменных. Область определения. Линии уровня. Частные производные. Градиент1. Найти D область определения функций: а). б). в). Решение.а). Логарифм по любому основанию существует только положительных величин. Значит, должно выполняться неравенство б). Функция Первая система неравенств определяет первую четверть координатной плоскости
а) б)
в) Рис. 8. в). Функция 2. Построить поверхности, заданные следующими уравнениями: а). в). е). Решение.а).Эта поверхность называется эллипсоидом. Построение ее выполняется с помощью сечений координатными плоскостями(рис. 9. а).
а) б)
в) гг г)
д) е)
ж) з)
Рис. 9. Система уравнений б). Заданная поверхность носит название однополостный гиперболоид. Для построения этой поверхности применим тот же метод, что и в пункте «а» (рис. 9. б). Систему
в).Такая поверхность называется двуполостным гиперболоидом, (рис. 9.в). Построена эта поверхность прежним методом, что и в предыдущих примерах. Система уравнений г). Поверхности такого типа называют конусом. Его вершина находится в начале координат, а за направляющую может быть взят эллипс д). Поверхность эта является примером эллиптического параболоида. Его вершина находится в начале координат. Сечения, параллельные оси Oz, – параболы; сечения, параллельные плоскости Oxy – эллипсы (рис. 9.д). е). Гиперболический параболоид – название поверхности этого примера. Сечения, параллельные плоскости ж). В этом примере поверхность является эллиптическим цилиндром (рис. 9. ж). На плоскости з). Эта поверхность – тоже цилиндр, но параболический, так как направляющей линией является парабола y = x2 (рис. 9.з). 3. Для значения
Рис. 10. 4. Построить поверхности уровней для и=0; 1 функции и=х2 + у2 + z2. Решение. Пусть Пусть и = 1, тогда 5. Вычислить пределы: а). Решение.а).При = Ответ. 2. б).
Ответ. 2. 6. При каком значении С z(x,y) функция будет непрерывной на всей плоскости
Решение.
Значит, C=0 при Ответ. 0. 7. Выяснить, когда функция
будет непрерывной. Решение. Функция Исследуем на непрерывность заданную функцию в точке Рассмотрим конкретно два направления из пучка прямых Тогда А это значит, что вдоль осей координат функция В результате имеем следующее: функция будет непрерывной в (0, 0) только по переменным Ответ. В точке (0, 0) функция имеет разрыв по совокупности переменных.
8. Найти частные приращения функций: а). Решение. К данным функциям применим формулы (1) и (2), получим а). б). 9. Найти частные производные функций а). Решение. В данных функциях фиксируем все переменные, кроме той, по которой вычисляем частную производную. Получаем в этом случае функцию одной переменной. Ее производная вычисляется по правилам дифференцирования и таблице производных. а). в). 10. Найти полное приращение функций: а). Решение.Применим формулу (8), получим: а). б). 11. Найти частные и полные дифференциалы функций: а). z = exy; б). z = x2+x y - Решение. Применим формулы дифференциалов
а).
б).
12. Найти частные производные первого порядка функции z = u2-v, где Решение. Применяя формулы типа (12), получим:
13. Найти полную производную функции Решение. Применяя формулу вида (11), получим:
= где x = t 3, y = t+1.
14. Функция у(х) задана уравнением cos2x+cos2y=1. Найти Решение. Вычисляя производную
15. Функция z(х, у) задана уравнением x2+y2+z2-2xyz = 1. Найти Решение. Обобщая формулу
Применяя их к заданной функции, имеем
16. Найти частные производные второго порядка функции Решение.
17. Проверить, что Решение.
Следовательно, получаем тождество 0=0.
Задания для аудиторной работы 1. Найти область определения функций: а). в). 2. Для значения 3. Указать точки или линии разрыва функций: а). 4. Является ли непрерывной функция:
5. Найти частные приращения функции:
6. Найти частные производные функций: а). z = xy2 -5x2 y-2y3 +3y-4x+2, б). u = s2 sin3t, в). z = ln(x3-y3), г). 7. Найти полное приращение и полный дифференциал функции: z = -2y2+xy+x2-3. 8. Найти полную производную функции 9. Найти где u = x siny; v = y cosx. 10. С помощью частных производных найти производную функции у(х), заданной неявно 11. Найти частные производные второго порядка функций: а). z = 3x y, б). z = x-ey, в). z=5y3-yx2+4y+x4; г). z = xarctgy. Семинарское занятие 4.2. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 ;
; ;
; .
. или
или  . Это неравенство геометрически изображает полуплоскость, расположенную по одну сторону от прямой
. Это неравенство геометрически изображает полуплоскость, расположенную по одну сторону от прямой  . Сама граница в область определения не включается. Область определения – открытое и неограниченное множество (рис. 8. а).
. Сама граница в область определения не включается. Область определения – открытое и неограниченное множество (рис. 8. а). будет существовать, если
будет существовать, если  . Из этого неравенства получаем следующее объединение
. Из этого неравенства получаем следующее объединение 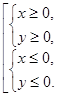 .
. , а вторая – третью четверть этой плоскости. Координатные оси входят в область определения D. Это множество неограниченное и замкнутое (рис. 8. б).
, а вторая – третью четверть этой плоскости. Координатные оси входят в область определения D. Это множество неограниченное и замкнутое (рис. 8. б).


 будет существовать тогда, когда подкоренное выражение будет положительным (равенство нулю недопустимо, так как корень находится в знаменателе дроби). Значит,
будет существовать тогда, когда подкоренное выражение будет положительным (равенство нулю недопустимо, так как корень находится в знаменателе дроби). Значит,  или
или  . Это неравенство описывает часть пространства R3, лежащее за пределами сферы
. Это неравенство описывает часть пространства R3, лежащее за пределами сферы  . Сама сфера к области определения не подключается. Следовательно, искомая область D является открытым и неограниченным множеством (рис. 8. в).
. Сама сфера к области определения не подключается. Следовательно, искомая область D является открытым и неограниченным множеством (рис. 8. в). ;б).
;б). ;
;  ;г).
;г). ;д).
;д). ;
; ; ж).
; ж). ;з).
;з).  .
.







 определяет на плоскости
определяет на плоскости  эллипс
эллипс 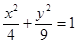 .Система уравнений
.Система уравнений  определяет на плоскости
определяет на плоскости  эллипс
эллипс  , а система уравнений
, а система уравнений  изображается на плоскости
изображается на плоскости  эллипсом
эллипсом  .
. мы уже рассматривали в предыдущем примере. Система уравнений
мы уже рассматривали в предыдущем примере. Система уравнений  на плоскости
на плоскости  .
.  - действительная ось гиперболы,
- действительная ось гиперболы,  - мнимая ось. Аналогично в плоскости
- мнимая ось. Аналогично в плоскости  определяет гиперболу
определяет гиперболу .В сечении плоскостью
.В сечении плоскостью  , параллельной плоскости
, параллельной плоскости  .
. описывает гиперболу на плоскости
описывает гиперболу на плоскости  – гипербола на плоскости
– гипербола на плоскости  описывает эллипс на плоскости
описывает эллипс на плоскости  построить линию уровня функции z=x/y.
построить линию уровня функции z=x/y. Решение.Эта функция существует при у ≠ 0, х
Решение.Эта функция существует при у ≠ 0, х  R. Уравнение линии уровня x/y = 1, у ≠ 0. Полученное уравнение в плоскости
R. Уравнение линии уровня x/y = 1, у ≠ 0. Полученное уравнение в плоскости  , тогда в пространстве
, тогда в пространстве  уравнение поверхности уровня
уравнение поверхности уровня  определяет точку О(0,0,0) –начало координат (сумма положительных величин равна нулю в том случае, если эти величины равны нулю).
определяет точку О(0,0,0) –начало координат (сумма положительных величин равна нулю в том случае, если эти величины равны нулю). – уравнение поверхности уровней описывает шар радиуса 1 с центром в начале координат трехмерного пространства
– уравнение поверхности уровней описывает шар радиуса 1 с центром в начале координат трехмерного пространства  , б).
, б).  .
. и
и  данное выражение дает неопределенность вида
данное выражение дает неопределенность вида  . Чтобы раскрыть эту неопределенность, надо и числитель и знаменатель умножить на выражение, сопряженное знаменателю. Получим
. Чтобы раскрыть эту неопределенность, надо и числитель и знаменатель умножить на выражение, сопряженное знаменателю. Получим  =
= =
= 


 =
= =0+2=2.
=0+2=2.
 .
. .
. .
.

 , если
, если  , существует на множестве
, существует на множестве  . В самой точке (0,0) функция равна нулю. Вычислим
. В самой точке (0,0) функция равна нулю. Вычислим  , получим, что
, получим, что  , то есть предел зависит от углового коэффициента
, то есть предел зависит от углового коэффициента  , что означает – предел не существует.
, что означает – предел не существует. , это
, это  и
и  .
. и
и  .
.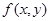 является непрерывной функцией.
является непрерывной функцией.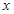 и
и  в отдельности и не является непрерывной по совокупности переменных.
в отдельности и не является непрерывной по совокупности переменных.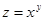 ; б).
; б). 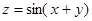 .
. ;
;  ;
; ;
;  ;
; ; б).
; б).  ; в).
; в).  .
. ;
;  ; б).
; б).  ;
;  ;
; ;
;  ;
;  .
. ; б).
; б).  .
. ;
; =
=  = =
= =  .
. .
.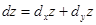 (полный),
(полный), 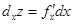 ,
, 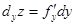 (частные).
(частные). ;
;  ;
; =
=  ;
; ;
;  ;
; .
. ; v = ln (x+y).
; v = ln (x+y).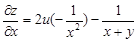 или
или  ;
; или
или  .
. , где x=t 3, y=t+1.
, где x=t 3, y=t+1. =
= =
=  ,
, .
.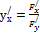 , получим
, получим или
или  .
. .
. ;
;  .
. =
=  ;
;  =
=  .
.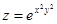 .
. ,
,  ;
;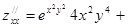
 ;
; 
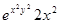 ;
;
 ;
; 
 для функции z = x siny.
для функции z = x siny. ;
;  ;
;  ;
; ;
;  ;
;  .
. ; б).
; б).  ;
; ; г)
; г)  .
. .
. ; б).
; б).  .
.

 .Обоснуйте ответ.
.Обоснуйте ответ. .
. .
. , где у = a cosx, z = sinx.
, где у = a cosx, z = sinx. ,
, .
.