
|
|
Лекция 4.2 «Функции нескольких переменных »Вопросы: 1.Частные производные высших порядков. 2.Локальный экстремум функции нескольких переменных (определение, признаки экстремума). Пусть частные производные функции Определение. Частные производные от частных производных
Производные
Теорема. Если функция Определение. Значение функции f(M) в точке М0 называется максимумом (минимумом), если оно является наибольшим (наименьшим) по сравнению с ее значениями во всех достаточно близких точках. Для локального максимума выполняется неравенство f(M0)> f(M) для всех точек М(х,у) из ρ-окрестности точки М0. Расстояние между М0 и М определяется по формуле Определение. Точки, в которых частные производные функции z = f(x, y) равны нулю или не существуют, называются критическими или стационарными.
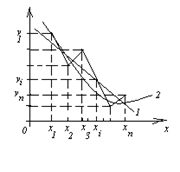
Рис. 1. Если функция нескольких переменных имеет экстремум, то это может быть только в точках, лежащих внутри области определения функции, в которых все ее частные производные первого порядка равны нулю или не существуют, то есть в критических точках. Теорема (необходимое условие экстремума). Если функция z=f(x,y) дифференцируемая в области существования и f(M0)> f(M) (f(M0) < f(M)) для всех точек М из ρ- окрестности точки М0, то частные производные первого порядка в этой точке равны нулю, то есть zx/(M0) = 0, zy/(M0) = 0. Критическая точка М0 будет точкой экстремума функции f(M), если для всех точек М, достаточно близких к М0, приращение функции ∆f= f(M) - f(M0) не меняет знака. Причем, если ∆f > 0, то точка М0 есть точка минимума, а если ∆f < 0, то М0 – точка максимума функции. Теорема(достаточные условия экстремума). Пусть точка М0 – критическая точка функции z = f(x, y), в которой функция дважды дифференцируема, то есть Понятия наибольшего и наименьшего значений функции многих переменных определяются так же, как и для функции одной переменной. Наибольшее или наименьшее из всех значений функции нельзя смешивать с максимумом или минимумом функции, которые являются наибольшим или наименьшим значением функции только по сравнению с ее значениями в соседних точках. Если функция разрывная или непрерывная в незамкнутой области, то она может не иметь ни наибольшего, ни наименьшего значения. Пусть функции z = f(x, y) (не нарушая общности рассуждений, ограничимся двумя переменными) определена и непрерывна в некоторой ограниченной замкнутой области D и имеет в этой области конечные частные производные. Тогда по теореме Вейерштрасса в этой области найдется точка М0 (х0,у0), в которой функция получает наибольшее (или наименьшее) из всех значений. Если точка М0 (х0,у0) лежит внутри области D, то в ней функция имеет максимум (минимум), а это означает, что точка М0 (х0,у0) – критическая. Однако своего наибольшего (наименьшего) значения функция z = f(x, y) может достигать и на границе области. Алгоритм поиска наибольшего и наименьшего значений функции: 1. Найти критические точки, лежащие внутри области D и вычислить значения функции в этих точках, не исследуя их на экстремум. 2. Найти наибольшее (наименьшее) значение функции на границе области D. 3. Сравнить полученные значения функции. Самое большое (меньшее) из них и будет наибольшим (наименьшим) значением функции во всей области D. Пусть в ходе исследования (например, покупательского спроса) получена следующая таблица, где х – аргумент (цена товара) у – функция (количество товара).
Требуется по этим данным получить функциональную зависимость (кривую спроса). Основываясь на графическом представлении (рис.2), эта зависимость может быть или линейная у = ах+b (1) или квадратичная Метод наименьших квадратов (МНК) предусматривает нахождение параметров a, b, c из условия min суммы квадратов отклонений. Рассмотрим линейную зависимость у = ах+b. В этом случае сумма квадратов отклонений вычисляется по формуле
Вычислим частные производные этой функции по переменным a и b, получим
Рис.2.
Учитывая необходимые условия экстремума, составим систему
Откуда находим a и b. Рассмотрим квадратичную зависимость y =ax2+bx+c. В этом случае сумма квадратов отклонений вычисляется по формуле
Вычислим частные производные этой функции по переменным a, b, c, и приравняем к нулю, получим следующую систему:
или
Откуда найдем a, b, c. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
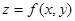 существуют на некотором промежутке D. Тогда они являются функциями аргументов x, y, которые могут быть непрерывными и иметь частные производные в точках множества D/.
существуют на некотором промежутке D. Тогда они являются функциями аргументов x, y, которые могут быть непрерывными и иметь частные производные в точках множества D/.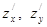 называются частными производными второго порядка и обозначаются
называются частными производными второго порядка и обозначаются ;
; 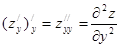 , (13)
, (13)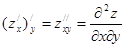 ;
; 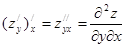 . (14)
. (14)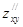 и
и  называются смешанными производными. Если функция f(M) имеет n аргументов, то общее число всего вторых частных производных равно n2, а число смешанных производных равно n2-n.
называются смешанными производными. Если функция f(M) имеет n аргументов, то общее число всего вторых частных производных равно n2, а число смешанных производных равно n2-n.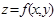 и ее частные производные
и ее частные производные 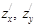 непрерывны на множестве D, то значение смешанной производной не зависит от порядка дифференцирования.
непрерывны на множестве D, то значение смешанной производной не зависит от порядка дифференцирования.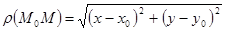 и является достаточно малым числом. Аналогично вводится понятие минимума. Максимумы и минимумы функции называются экстремумами, а точка М0 (х0,у0) – экстремальной точкой.
и является достаточно малым числом. Аналогично вводится понятие минимума. Максимумы и минимумы функции называются экстремумами, а точка М0 (х0,у0) – экстремальной точкой.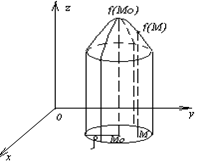
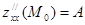 ,
, 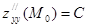 ,
,  . Тогда, если ∆ = АС - В2 имеет положительный знак, то в точке М0 есть экстремум, причем, если А>0 (С>0 при А = 0), то минимум, если А<0 (С<0 при А = 0), то максимум. Если же ∆< 0, то экстремума нет. При ∆ = 0 требуются дополнительные исследования.
. Тогда, если ∆ = АС - В2 имеет положительный знак, то в точке М0 есть экстремум, причем, если А>0 (С>0 при А = 0), то минимум, если А<0 (С<0 при А = 0), то максимум. Если же ∆< 0, то экстремума нет. При ∆ = 0 требуются дополнительные исследования.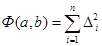 =
= 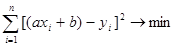
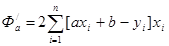 ,
,  .
.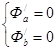 или
или 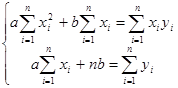 .
.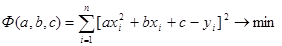 .
.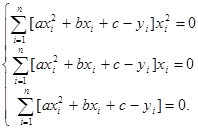
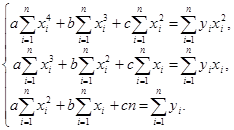 .
.