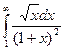|
|
Лабораторной работы на ЭВМ
Задание № 1.
1. Построение графиков функций:
2. Решение уравнений и систем уравнений: а) 3. Векторы:
а) б) в)
4. Найти f(x) и собственные числа матрицы f(x) f(x)= 5. Пределы а)
6. Найти производную: а) y= в)
д) z= 7. Интегралы: а)
г)
8. Комплексные числа, полиномы: а) Построить в (Re W, Im W) годограф: W= б) Вычислить корни и построить их в (Re,Im):
9. Исследовать сходимость рядов: а) в) Разложить в ряд Тейлора в окрестности г) Разложить в ряд Фурье в указанном интервале:
10. Решить дифференциальные уравнения и системы уравнений: а)
б) в)
Значения параметров для исследования динамической системы, описывающей малые колебания математического маятника. Задание сформулировано в разделе 2.3 настоящего пособия
Задание № 2.
1. Построение графиков функций:
2. Решение уравнений и систем уравнений: а) 3. Векторы:
а) б) в)
4. Найти f(x) и собственные числа матрицы f(x) f(x)= 5. Пределы а)
6. Найти производную: а) y= в)
д) z= 7. Интегралы: а) г)
8. Комплексные числа, полиномы: а) Построить в (Re W, Im W) годограф: W=
б) Вычислить корни и построить их в (Re,Im):
9. Исследовать сходимость рядов: а) в) Разложить в ряд Тейлора в окрестности г) Разложить в ряд Фурье в указанном интервале:
10. Решить дифференциальные уравнения и системы уравнений: а) в)
Значения параметров для исследования динамической системы, описывающей малые колебания математического маятника. Задание сформулировано в разделе 2.3 настоящего пособия
Задание № 3. 1. Построение графиков функций:
2. Решение уравнений и систем уравнений: а) 3. Векторы:
а) б) в)
4. Найти f(x) и собственные числа матрицы f(x) f(x)= 5. Пределы
а)
6. Найти производную: а) y=x+ в) д) z=arcsin
7. Интегралы а)
г)
8. Комплексные числа, полиномы:
а) Построить в (Re W, Im W) годограф: W= б) Определить НОД полиномов:
9. Исследовать сходимость рядов: а) в) Разложить в ряд Тейлора в окрестности г) Разложить в ряд Фурье в указанном интервале:
10. Решить дифференциальные уравнения и системы уравнений:
а) б) в) Значения параметров для исследования динамической системы, описывающей малые колебания математического маятника. Задание сформулировано в разделе 2.3 настоящего пособия
Задание № 4.
1. Построение графиков функций:
2. Решение уравнений и систем уравнений: а) (
3. Векторы:
а) б) в)
4. Найти f(x) и собственные числа матрицы f(x)
5. Пределы
а)
6. Найти производную: а) в) д) 7. Интегралы а) г)
8. Комплексные числа, полиномы: а) Построить в (Re W, Im W) годограф:
9. Исследовать сходимость рядов: а)
в) Разложить в ряд Тейлора в окрестности
10. Решить дифференциальные уравнения и системы уравнений: а) б)
в)
Значения параметров для исследования динамической системы, описывающей малые колебания математического маятника. Задание сформулировано в разделе 2.3 настоящего пособия
Задание № 5.
1. Построение графиков функций:
2. Решение уравнений и систем уравнений. а)
3. Векторы.
а) б) в)
4. Найти F(x) и собственные числа матрицы F(x).
5. Пределы. а)
6. Производные. а) в) д) 7. Интегралы а)
г)
8. Комплексные числа, полиномы.
а) Построить в (ReW, ImW) годограф б) Определить НОД полиномов.
9. Исследовать сходимость рядов а)
в) Разложить в ряд Тейлора функции в окрестности x0. г) Разложить в ряд Фурье в указанном интервале.
10. Решить дифференциальные уравнения и системы уравнений.
а) б) в) Значения параметров для исследования динамической системы, описывающей малые колебания математического маятника. Задание сформулировано в разделе 2.3 настоящего пособия
Задание № 6.
1. Построить графики функций:
2. Решение уравнений и систем уравнений: а) (x+1)(x+2)(x+3)(x+4)=120; б)
3. Векторы: а) б) в)
Найти f(x) = 4. Найти собственные числа матрицы f(x).
5. Пределы а)
6. Найти производную: а) y=sin(cos2x)cos(sin2x) в) д) z=
7. Интегралы: а) г)
8. Комплексные числа, полиномы:
а) Построить в (Re W, Im W) годограф: W= б) Определить Н.О.Д. полиномов: P6(x) =
9. Исследовать сходимость рядов:
а) в) Разложить в ряд Тейлора в окрестности г) Разложить в ряд Фурье в указанном интервале:
10. Решить дифференциальные уравнения и системы уравнений:
а) б) в)
Значения параметров для исследования динамической системы, описывающей малые колебания математического маятника. Задание сформулировано в разделе 2.3 настоящего пособия
Задание № 7.
1. Построить графики функций.
2. Решение уравнений и систем уравнений. а) ( 3–x)4+(2–x)4=(5–2x)4 б) 3. Вектора. а) б) в)
4. Найти f(X )= x2+2x+3 , если X=
5. Пределы. a)
6. Производные.
а) y = 1/cos5 x, г) x2/4+y2/9 =1,
7. Интегралы. а) г)
8. Комплексные числа, полиномы.
a) Построить в (Re w,Im w) годограф : w=
б) Определить НОД полиномов: p5(x) = x5–10x4–x1
9. Исследовать сходимость рядов.
а) в) Разложить ряд Тейлора в окрестности x0: y= г) Разложить в ряд Фурье в указанном интервале:
10. Решить дифференциальные уравнения и системы уравнений.
a) в)
Значения параметров для исследования динамической системы, описывающей малые колебания математического маятника. Задание сформулировано в разделе 2.3 настоящего пособия
Задание № 8.
1. Построить графики функций: а) y= б) y= в) z =x3+ г) д)
2. Решение уравнений и систем уравнений: а) x4+1=2(1+x)4; б) 3. Векторы:
а) б) в)
4. Найти f(x) и собственные числа матрицы f(x)
f(x)=
5. Пределы а)
6. Найти производную: а) y=tg в) д) Z= 7. Интегралы: а) г) 8. Комплексные числа, полиномы: а) Построить в (Re W, Im W) годограф: W= б) Определить Н.О.Д. полиномов: P4(x) =
9. Исследовать сходимость рядов: а)
в) Разложить в ряд Тейлора в окрестности г) Разложить в ряд Фурье в указанном интервале:
10. Решить дифференциальные уравнения и системы уравнений:
а)
в)
Значения параметров для исследования динамической системы, описывающей малые колебания математического маятника. Задание сформулировано в разделе 2.3 настоящего пособия
Задание № 9.
1. Построить графики функций: а) y=
д)
2. Решение уравнений и систем уравнений:
а)
б)
3. Векторы:
а) б) в)
4. Найти f(x)= x =
5. Пределы а) б)
6. Найти производную: а) y=
в)
д) z= 7. Интегралы:
а)

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|



 y
y 
 t
t 
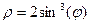

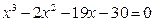 б)
б) 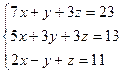
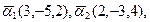 Найти
Найти 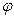 =угол
=угол 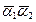
 Найти
Найти 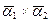 – векторное
– векторное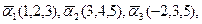 Найти
Найти 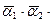
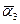 – смешанное
– смешанное X =
X = 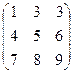
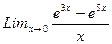 б)
б) 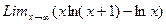

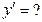 б)
б) 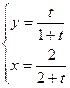
 =?
=?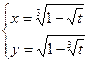
 г)
г) 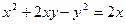
 =?
=?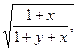
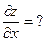
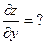
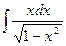 б)
б) 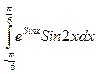 в)
в) 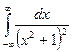
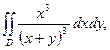 D:
D: 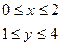 д)
д) 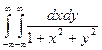

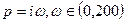 ;
;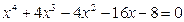
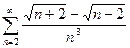 б)
б) 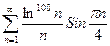
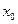 : y=
: y= 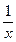 ,
, 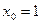
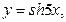
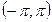
 ,
, 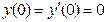
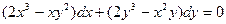
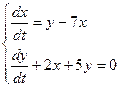

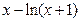
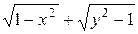
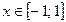 y
y 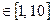
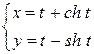 t
t 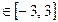
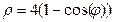
 б)
б) 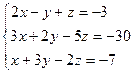
 Найти
Найти 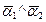
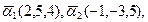 Найти
Найти 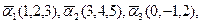 Найти
Найти  x=
x= 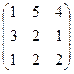
 б)
б) 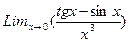


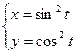
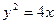
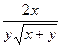
 б)
б) 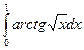 в)
в) 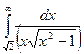
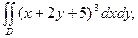 D:
D:  д)
д) 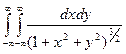
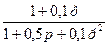
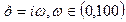
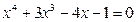 .
. б)
б) 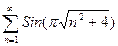
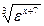 ,
, 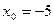
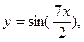
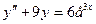 ,
, 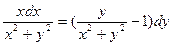



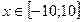
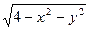

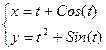 t
t 
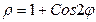

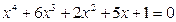 б)
б) 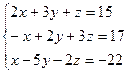
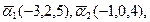 Найти
Найти  Найти
Найти  Найти
Найти 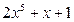 x=
x= 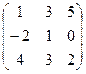
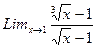 б)
б) 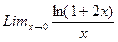

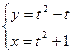
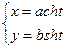


 б)
б)  в)
в) 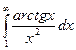
 D:
D: 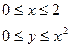 д)
д) 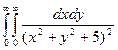
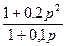
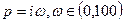

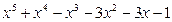

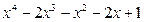
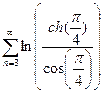 б)
б) 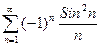
 ,
, 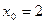
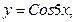
 ,
, 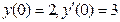
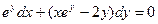
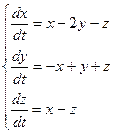
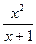


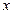 -
- 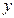 )
)
 [-10,-2]
[-10,-2]
 t
t  [-2,2]
[-2,2]
 5(1+cosφ),
φ
5(1+cosφ),
φ  +
+ 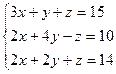

 угол между
угол между 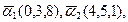 найти
найти  найти
найти  – смешанное произведение
– смешанное произведение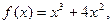
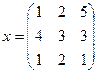
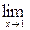
 б)
б) 
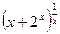

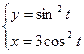 ,
, 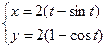 ,
, 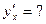 г)
г) 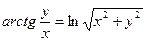
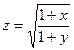 ,
,  ,
, 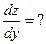
 б)
б)  в)
в) 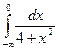
 D:
D: 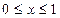 ,
, 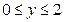 д)
д) 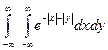
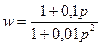 ,
, 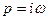 ,
, 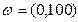
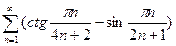 б)
б) 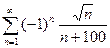
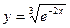 ,
, 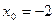
 ,
, 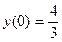 ,
, 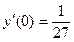

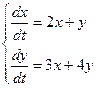
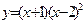
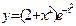
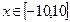
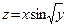
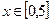

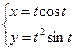

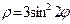 ,
,
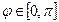
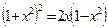 б)
б) 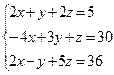
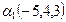 ;
;  ; найти угол между векторами
; найти угол между векторами 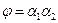
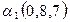 ;
;  ; найти векторное произведение
; найти векторное произведение 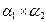
 ;
; 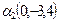 ;
; 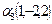 ; найти смешанное произведение
; найти смешанное произведение 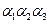


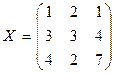
 б)
б) 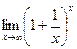
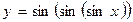 ,
,  б)
б) 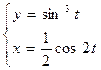 ,
, 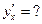
 ,
,  г)
г) 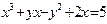 ,
, 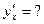
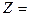
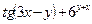 ,
, 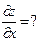 ,
, 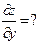
 б)
б)  в)
в) 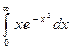
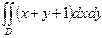 D:
D:  д)
д) 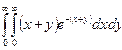
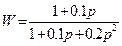 ,
,  ,
, 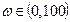

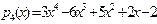
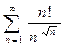 б)
б) 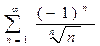
 ,
, 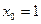
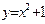 ,
, 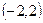
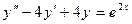 ,
,  ,
, 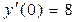
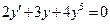
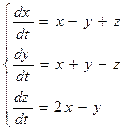
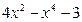
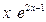
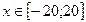 y
y 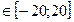

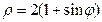 ,
,
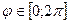
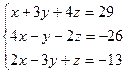
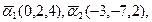 Найти
Найти  Найти
Найти 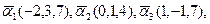 Найти
Найти  , если x =
, если x = 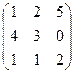 .
.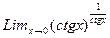 б)
б) 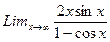
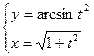
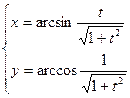
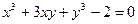
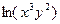
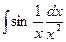 б)
б) 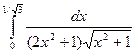 в)
в) 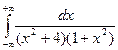
 D:
D: 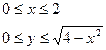 д)
д) 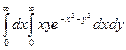
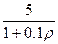
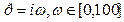
 ; P5(x) = 3x5–7x3+3x2–7;
; P5(x) = 3x5–7x3+3x2–7;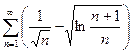 б)
б) 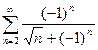
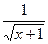 ,
, 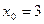
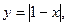
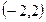
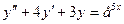 ,
, 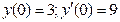
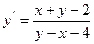
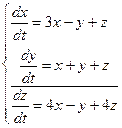

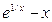
 y
y 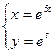 t
t 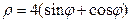 ,
,
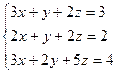
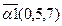 ,
, 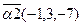 . Найти
. Найти 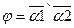 .
.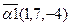 ,
,  . Найти
. Найти  – векторное произведение.
– векторное произведение.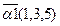 ,
,  ,
, 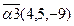 . Найти
. Найти 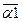
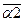
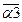 – смешанное произведение.
– смешанное произведение.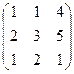 , Найти собственные числа матрицы f(X).
, Найти собственные числа матрицы f(X).
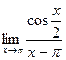
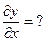 , б)
, б) 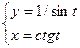 ,
,  ,
, 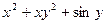 ,
, 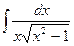 б)
б) 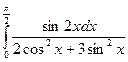 в)
в) 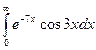
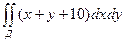 D:
D: 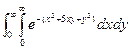
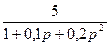 ,
, 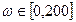
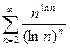 б)
б) 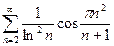
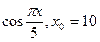
 ,
, 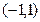
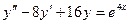
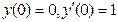 б)
б) 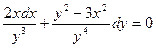
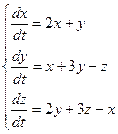
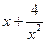 ;
; 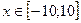
 ;
; 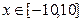
 ;
; 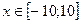 y
y 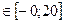
 t
t 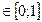
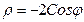 ;
; 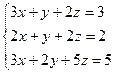
 Найти
Найти 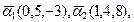 Найти
Найти 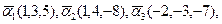 Найти
Найти 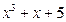 , x=
, x= 
 б)
б) 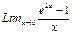
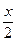
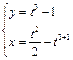
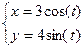
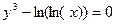

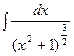 б)
б) 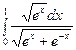 в)
в) 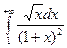
 D:
D: 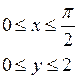 д)
д) 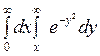

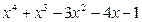 ; P3(x) = x3+x2–x;
; P3(x) = x3+x2–x;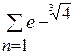 б)
б) 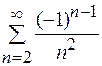
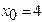
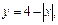
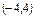
 б)
б) 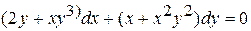
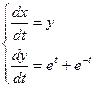
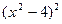 б) y=
б) y= 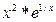 в) z =
в) z = 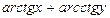 г)
г) 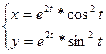
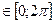
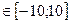
 ;
; 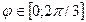
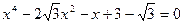
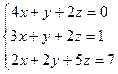
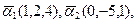 Найти
Найти 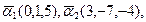 Найти
Найти 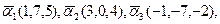 Найти
Найти 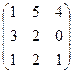 Найти собственные числа матрицы f(x).
Найти собственные числа матрицы f(x).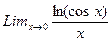
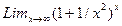
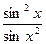
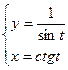

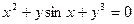
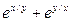
 б)
б) 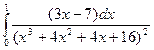 в)
в)