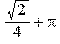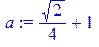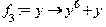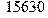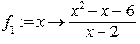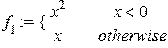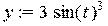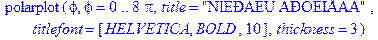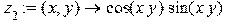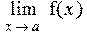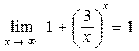|
|
Warning, the name changecoords has been redefinedС.Н. Стребуляев, Д.Ю. Васин ИСПОЛЬЗОВАНИЕ СИСТЕМЫ АНАЛИТИЧЕСКИХ ВЫЧИСЛЕНИЙ MAPLE ДЛЯ РЕШЕНИЯ ЗАДАЧ ПРИКЛАДНОЙ МАТЕМАТИКИ
Рекомендовано методической комиссией факультета вычислительной математики и кибернетики для студентов высших учебных заведений, обучающихся по направлению подготовки 010501, 010500.62 «Прикладная математика и информатика»
Нижний Новгород УДК 519. (075) ББК В19 С-84
С-84 Стребуляев С.Н., Васин Д.Ю. Использование системы аналитических вычислений Maple для решения задач прикладной математики: Учебное пособие. – Нижний Новгород: Издательство Нижегородского госуниверситета, 2007. с.
Рецензент: доктор физ.-мат. наук, профессор Ю.Л. Кетков
В пособии приведены алгоритмы, программные средства, подходы, которые в течение нескольких лет использовались авторами пособия для решения конкретных задач прикладной математики при проведении лабораторных занятий и самостоятельной работы со студентами дневного и вечернего отделений факультета ВМК ННГУ. Представленный материал служит для закрепления лекционного материала и способствует более эффективному использованию вычислительной техники при решении конкретных задач динамики систем, теории колебаний и теории автоматического регулирования при выполнении лабораторных работ, курсовых и дипломных проектов, а также, в процессе научных исследований при моделировании динамических систем и процессов.
УДК 519. (075) ББК В19
© Нижегородский государственный университет им. Н.И. Лобачевского, 2007
ОГЛАВЛЕНИЕ Введение ......................................................................................................... 4
1. Основные пакеты, операторы и функции системы аналитических вычислений Maple ........................................................................................................... 6 1.1. Пакеты функций .............................................................................. 6 1.2. Способы задания функций и построения их графиков ............... 11 1.3. Вычисление пределов ................................................................... 28 1.4. Вычисление производных ............................................................ 30 1.5. Вычисление интегралов ................................................................ 36 1.6. Операции с рядами ....................................................................... 43 1.7. Решение уравнений, неравенств и их систем ............................... 54 1.8. Анализ функций ............................................................................ 63 1.9. Решение дифференциальных уравнений и их систем .................. 72 1.10. Операции с векторами и матрицами .......................................... 90 1.11. Преобразование комплексных чисел, аналитических выражений и функций комплексного переменного .................................................. 101
2. Примеры использования САВ Maple для решения прикладных задач 107 2.1. Расчет показателей динамического качества системы электропривода 108 2.2. Расчет собственных и вынужденных колебаний легкового автомобиля ....................................................................................................... 118 2.3. Изучение фазового портрета математического маятника. Исследование явления резонанса ....................................................................... 133
3. Контрольные задания для выполнения лабораторной работы на ЭВМ 142
Список использованных источников ......................................................... 190
Приложение ................................................................................................ 192
ВВЕДЕНИЕ
Одним из этапов процесса математического моделирования является разработка программного обеспечения. Этому этапу в цепочке «объект — расчетная схема — математическая модель — программное обеспечение — анализ результатов на ЭВМ» уделяется всегда много внимания. При разработке программного обеспечения на первом этапе проводится отладка собственно этого обеспечения. На втором этапе, с использованием этого обеспечения, выполняется наиболее ответственная работа — идентификация параметров математической модели. Поэтому к программному обеспечению предъявляются повышенные требования при работе с ним пользователя: удобный интерфейс, высокая скорость при проведении расчетов, наличие синтаксического и семантического контроля при задании входных параметров и другие. Современные возможности персональных ЭВМ по быстродействию, объему памяти, насыщенности программными средствами позволяют моделировать сложные динамические системы, избегая упрощения (иногда необоснованного) их математических моделей. Динамика роста вычислительных возможностей современных компьютеров достаточно высока и позволяет надеяться на успешное решение все более сложных задач. Наряду с языками программирования, появились и системы аналитических вычислений (САВ): Maple, Mathematica, Matlab и другие. Использование САВ (систем компьютерной алгебры с расширенными возможностями в области символьных вычислений) еще в большей степени, чем языки программирования, позволяет автоматизировать процесс написания программ. Особое место среди САВ занимает система Maple /1/. Системы компьютерной математики класса Maple были созданы корпорацией Waterlo Maple, Inc. (Канада) как системы компьютерной алгебры с расширенными возможностями в области символьных вычислений. Maple — типичная интегрированная система. Она объединяет в себе: — мощный язык программирования; — редактор для подготовки и редактирования документов и программ; — современный многооконный пользовательский интерфейс с возможностями работы в диалоговом режиме; — мощную справочную систему со многими тысячами примеров; — ядро алгоритмов и правил преобразования математических выражений; — численный и символьный процессоры; — систему диагностики; — библиотеки встроенных и дополнительных функций; — пакеты функций сторонних производителей и поддержку некоторых других языков программирования и программ. При рассмотрении большого числа публикаций, посвященных описанию САВ Maple, часто употребляется термин «…мощный язык, справочная система…» и другие, что на самом деле соответствует действительности. Опыт работы авторов настоящего пособия подтверждает это. Например, при решении ряда сложных задач динамики систем, связанных с преобразованием громоздких выражений, пришлось отказаться от использования языка программирования Fortran в пользу системы аналитических вычислений Maple. При написании настоящего пособия использованы материалы, приведенные в списке использованных источников, описаны примеры использования системы, полученные авторами, при решении конкретных задач. В первом разделе дается краткое описание возможностей системы и примеры их использования. Во втором — рассматриваются математические модели конкретных систем и комплексы программ их расчета. В третьем разделе приведены контрольные задания к лабораторной работе
1. ОСНОВНЫЕ ПАКЕТЫ, ОПЕРАТОРЫ И ФУНКЦИИ СИСТЕМЫ АНАЛИТИЧЕСКИХ ВЫЧИСЛЕНИЙ MAPLE
В настоящем разделе описаны возможности системы для решения задач из различных разделов математики: математического анализа, алгебры, геометрии, теории функций и других. Дано краткое описание пакетов и приведены примеры использования функций для решения различных задач: построения графиков функций, вычисления пределов, производных и интегралов, операций с рядами, решения уравнений, неравенств и их систем, анализ функций, решение дифференциальных уравнений, операции с векторами и матрицами и преобразование комплексных чисел и выражений. Эти примеры взяты из известных задачников для различных разделов математики с тем, чтобы пользователь мог проконтролировать правильность решения задачи с использованием функции системы Maple.
1.1. Пакеты функций Основой для работы с символьными преобразованиями в Maple является ядро системы. Оно содержит сотни базовых функций и алгоритмов символьных преобразований. Объем ядра достигает 6–7 Мбайт. Имеется также основная библиотека операторов, команд и функций. Многие встроенные в нее функции, как и функции ядра, могут использоваться без какого-либо объявления, другие нуждаются в объявлении. Множество функций, в том числе применяемых довольно редко и в вычислениях специальных видов, реализовано в проблемно-ориентированных, подключаемых пакетах расширения (packages). Подключение пакета осуществляется с помощью команды: with(название пакета). Описание наиболее часто употребляемых пакетов начнем с пакета двумерной и трехмерной графики plots. Пакет plots содержит полсотни графических функций, существенно расширяющих возможности построения двумерных и трехмерных графиков. Среди этих функций следует отметить средства построения ряда новых типов (в виде линий уровня, векторных полей и других), а также средства объединения нескольких графиков в одном. Особый интерес, при рассмотрении задач динамики систем, представляют функции, обеспечивающие анимацию как двумерных так и одномерных графиков. Ниже приведено обращение к пакету графики и перечень функций включенных в этот пакет. >restart: > with(plots);
Уникальной возможностью системы Maple является возможность решения задач линейной алгебры в символьном виде. Реализованы также численные методы решения задач линейной алгебры, которые широко используются в основных сферах ее приложения — математическом моделировании, динамике систем, теории управления и других. Пакет решения задач линейной алгебры linalg один из самых обширных и мощных пакетов в этой области. Для просмотра функций содержащихся в этом пакете достаточно использовать команду: > with(linalg);
В новых реализациях системы была сделана ставка на использование быстрых алгоритмов линейной алгебры. Их применение обеспечивает эффективное использование систем символьной математики в решении задач, сводящихся к задачам линейной алгебры. Указанные программные средства реализованы в пакете LinearAlgebra. Для загрузки этого пакета используется команда: > with(LinearAlgebra);
Пакет CurveFitting осуществляет процедуру приближения кривых. Он содержит ряд функций:
Ø with(CurveFitting); Ø
К числу этих функций относятся: функция для вычисления В-сплайновых кривых, полиномиальная и сплайновая аппроксимация, метод наименьших квадратов, функции рациональной аппроксимации и аппроксимации непрерывными дробями, аппроксимация рядом Тейлора и полиномиальная, полиномами Чебышева и аппроксимация Чебышева-Паде. Для расширенной поддержки интегральных преобразований служит пакет inttrans. Этот пакет вызывается командой:
Ø with(inttrans); Ø
и содержит набор функций, охватывающий такие практически важные области математики, как ряды Фурье, прямые и обратные преобразования Фурье, Лапласа и Гильберта, интегральные преобразования Ханкеля и Меллина. Пакет student — один из пакетов наиболее привлекательный для студентов и аспирантов. В нем собраны наиболее распространенные и нужные функции, используемые в своей практической работе этой категорией пользователей.
Ø with(student); Ø
Ортогональные полиномы находят самое широкое применение в различных математических расчетах при составлении алгоритмов интерполяции, экстраполяции различных функциональных зависимостей, где свойство ортогональности обеспечивает высокую оценку погрешности. В пакете orthopoly содержатся следующие ортогональные полиномы: Гегенбауэра, Эрмита, Лагера, Лежандра, Якоби и Чебышева. Пакет вызывается командой: > with(orthopoly);
Пакет VectorCalculus открывает доступ ко многим командам и функциям векторного анализа, теории поля и приложений дифференциального исчисления. Этот пакет ориентирован в первую очередь на решение задач математической физики, использующих методы теории поля и приложения дифференциального исчисления. Вызов этого пакета осуществляется командой:
Ø with(VectorCalculus); Ø
Следует отметить, что данный пакет после загрузки видоизменяет многие операторы, команды и функции, встроенные в ядро системы. Поэтому пользоваться пакетом надо с известной степенью осторожности. Для восстановления роли функций можно использовать команду restart. Для выполнения ряда специальных операций с полиномами или создания полиномов с заданными свойствами служит пакет Polynomial Tools. Этот пакет имеет небольшое число функций:
Ø with(PolynomialTools); Ø
В пакет входят функции расщепления, сортировки и преобразования полиномов и другие. Решение дифференциальных уравнений самых различных типов — одно из достоинств системы аналитических вычислений Maple. Пакет DEtools предоставляет ряд полезных функций для решения дифференциальных уравнений и систем уравнений:
Ø with(DEtools); Ø
Этот пакет дает самые изысканные средства для аналитического и численного решения дифференциальных уравнений и их систем. Для решения дифференциальных уравнений с частными производными и его визуализации служит специальный инструментальный пакет PDEtools:
Ø with(PDEtools); Ø
Большое количество физических констант, используемых в расчетах, задаются с использованием следующего пакета:
Ø with(ScientificConstants); Ø
> GetConstant(g);
> g:=evalf(Constant(g,units));
В настоящем разделе приведена лишь незначительная часть пакетов прикладных программ используемых для решения задач указанного выше класса. Информацию о других пакетах можно получить в справочнике системы Maple, а также в многочисленной литературе, посвященной описанию данной системы.
1.2. Способы задания функций и построение их графиков В системе аналитических вычислений Maple существует четыре способа задания функций. Способ 1. Определение функции с помощью оператора присваивания (:=), например > restart; > f[1]:=sin(x)^3+1;
Для того чтобы вычислить значение функции в какой либо точке, необходимо выполнить следующих два оператора: > x:=Pi/4; f[1];
> 1/4*2^(1/2)+Pi;
После выполнения этих команд переменная x имеет заданное значение Pi/4. Чтобы насовсем не присваивать переменной конкретного значения, удобнее использовать команду подстановки subs в следующем виде:
> a:=subs({x=Pi/4},f[1]);
Чтобы получить приближенное значение предыдущего выражения в виде числа с плавающей запятой, используем команду:
> evalf(%); # Символ (%) используется для вызова предыдущей команды;
Способ 2. Определение функции с помощью функционального оператора, который ставит в соответствие независимой переменной (аргументу) значение зависимой переменной (функции):
> f[2]:=(t)->t^3+exp(t);
Обращение к этой функции осуществляется привычным для специалистов способом:
> f[2](1); f[2](3);
Приближенные значения получим в виде:
> evalf(f[2](1)); evalf(f[2](3));
Способ 3. Задание функции с помощью команды unapply
> f[3]:=unapply(y^6+y,y);
> f[3](1); f[3](5);
Способ 4. Задание кусочно-линейной функции. Например:
> f[4]:=piecewise(z<0,1,z>=0 and z<1, z, z>=1,cos(z));
Приведенные выше способы задания функций применимы и для случая функций от нескольких переменных. Для построения графиков функций используется пакет plots. Она задается в виде plot(f,h,v,g), где f — визуализируемая функция, h — аргумент функции, с указанием области его изменения, v — необязательная переменная — функция, с указанием области ее изменения, g — набор параметров, задающих стиль построения графика функции. Для двумерного графика возможны следующие наиболее часто употребляемые параметры (g): axes — определяет тип координатных осей, допускает значения: frame, boxed, normal, none; axesfont — определяет шрифт для отображения надписей координатной шкалы, тип шрифта (times,courier,helvetica,symbol), его стиль (bold, italic, bolditalic), а также размеры; color — цвет линии для отображения графика функции: aquamarine (зеленовато-голубой), black (черный), blue (голубой), navy (темно-синий), coral (светло-красный), cyan (голубой), brown (коричневый), gold (ярко-желтый), green (зеленый), gray (серый), khaki (хаки), magenta (пурпурный), maroon (красно-коричневый), orange (оранжевый), pink (розовый), plum (темно-фиолетовый), red (красный), sienna (охра), tan (желто-коричневый), turquoise (бирюзовый), violet (фиолетовый), wheat (бледно-желтый), white (белый), yellow(желтый); coords — параметр задает систему координат, в которой отображается график: декартова система координат (cartesian) — по умолчанию, биполярная (bipolar), кардиоидная (cardioid), кассинианова (cassinian), эллиптическая (elliptic), гиперболическая (hyperbolic), инверсная кассинианова (invcassinian), инверсная эллиптическая (invelliptic), логарифмическая (logarithmic), логарифмо-гиперболическая (logcosh), максвелова (maxwell), параболическая (parabolic), полярная (polar), круговая (rose) и касательная (tangent); discont — если формальный параметр функции discont( ) равен true, то выполняется проверка функции на наличие точек разрыва, по умолчания значение параметра равно false; font — параметр определяет шрифт для отображения текстовых надписей (times, courier, helvetica или symbol) и стиля шрифта (roman, bold, italic, bolditalic) на графике; labels — параметр задает надписи для осей координат; параметр задается в виде двух строк : для оси абсцисс и для оси ординат; labelfont — параметр определяет шрифт надписей для осей координат; legend — легенда графика, для нескольких графиков задается список, каждый элемент которого — легенда соответствующего графика; linestyle — стиль линии: сплошная (solid), пунктирная (dot), штрихованная (dash), штрихпунктирная (dashdot); numpoints — параметр задает минимальное число базовых точек для построения графика (по умолчанию это число равно 50); scaling — параметр задает масштабы по осям координат отображения графика: единый (constrained) и различный (unconstrained); style — параметр стиля линии: линия (line), точка (point), заливка (patch), заливка без отображения границ (patchnogrid); symbol — тип символов для отображения базовых точек: квадрат (box), крест (cross), круг (circle), точка(point), ромб (diamond); symbolsize — размер символов отображения базовых точек (по умолчанию он равен 10); title — заголовок рисунка; titlefont — шрифт заголовка рисунка; thickness — параметр, задающий толщину линии отображения графика(0–15). Ниже приведены примеры построения графиков функций, заданных в разных формах. > restart: with(plots): Warning, the name changecoords has been redefined
Для случая функции, заданной в явном виде, построение графика осуществляется следующим образом:
> f[1]:=(x)->(x^2-x-6)/(x-2);
> plot(f[1](x),x=1..3,color=red,thickness=2);
Если задать ограничения на изменение значения функции, графический образ рассматриваемой функции будет более понятным: > plot(f[1](x),x=-2..6,y=-50..50,color=red,thickness=2);
Аналитически заданная функция может быть также использована в операторе plot: > plot((x^2-x-6)/(x-2),x=1..3,y=-50..50,thickness=2);
Предел изменения аргумента может быть бесконечным (infinity). > plot(ln(1+cos(x)),x=0..infinity,color=blue,thickness=2);
> plot(ln(1+cos(x)),x=0..infinity,y=-5..0,color=blue,thickness=2);
Для функции с разрывами возможно построение непрерывного графика discont=true (по умолчанию discont=false): > plot(ln(1+tan(x)),x=-10..10,discont=true,color=gold,thickness=2);
> plot(ln(1+tan(x)),x=-10..10,color=gold,thickness=2);
Построение нескольких графиков функций в одних осях осуществляется следующим образом:
Ø plot([sin(x),sin(x)/x,sin(x^3/100)], x=-10..10,color=red,thickness=2);
> plot([sin(x),sin(x)/x,sin(x^3/100)], x=-10..10,color=[black,blue,red], style=[line,line,point],thickness=2);
Построение графика функции, заданной отдельными точками, осуществляется следующим образом: > restart: > p:=[[i,sin(i/3)]$i=1..30]:# -процедура задающая последовательность точек; > plot(p,x=0..30,color=black,style=point,symbol=circle,symbolsize=20,thickness=4);
Ø plot([[0,0],[1,0.5],[2,0.7],[3,0.4],[5,0.2]],x=0..5,style=line,symbol=circle,color=blue,thickness=2);
Ø plot([[0,0],[1,0.5],[2,0.7],[3,0.4],[5,0.2]],x=0..5,style=point,symbol=circle,color=black,thickness=4);
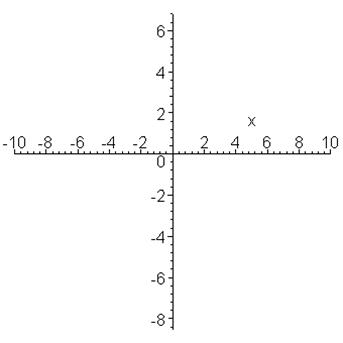
Построение графиков функций, заданных значениями элементов вектора: > restart: > x:=[0,1,2,3,4,5,6,7]: y:=[2,1.79,1.27,0.571,-0.2,-0.678,-0.758,-0.538]: > > pare:=(x,y)->[x,y];
> Coordxy:=zip(pare,x,y,2);
> plot(Coordxy,style=[line,point],symbol=circle,axes=boxed,thickness=2);
Построение графика функции, заданной процедурой: > restart: > w:=proc(x) if sin(x)>0 then sin(x) else -sin(x) fi end;
Ø plot(w,-15..15,color=black,thickness=2);
Построение графиков кусочно-линейных функций: > restart: > f[1]:=piecewise(x<0,x^2,x);
> plot(f[1],x=-10..10,color=black,thickness=2);
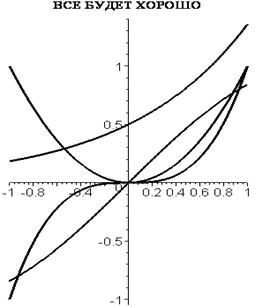
Построение графиков функций заданных функциональными операторами и встроенными функциями: > restart: > plot([exp/2,sin,x->x^2,x->x^3],-1..1,color=black,thickness=3,title="ВСЕ БУДЕТ ХОРОШО",titlefont=[TIMES,BOLD,10]);
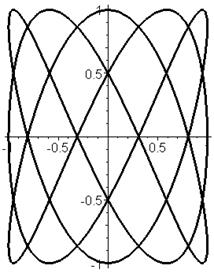
Построение графиков функций, заданных параметрически: > restart: > plot([sin(3*t),cos(5*t),t=0..2*Pi],color=black,thickness=3);
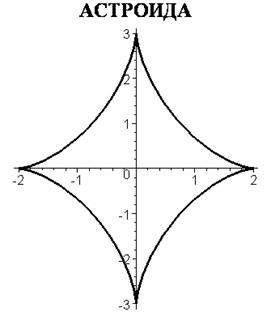
> x:=2*(cos(t)^3);y:=3*(sin(t)^3);
Ø plot([x,y,t=0..2*Pi],color=orange,title="АСТРОИДА",titlefont=[TIMES,BOLD,15],thickness=3);
Построение графиков функций, заданных в полярной системе координат: > restart: > plot([2*(1-cos(phi)),phi,phi=0..2*Pi],color=black,coords=polar,title="КАРДИОИДА", titlefont=[TIMES,BOLD,15],thickness=3);
> polarplot(phi,phi=0..8*Pi,title="СПИРАЛЬ АРХИМЕДА",titlefont=[HELVETICA,BOLD,10],thickness=3);
Построение графика функции заданной в неявном виде: > restart:with(plots): implicitplot(x^3+y^3-2*x*y=0, x=-2..1.5,y=-2..2,color=green,title="ДЕКАРТОВ ЛИСТ",titlefont=[HELVETICA,BOLD,10],numpoints=10000,thickness=3);
> Построение графиков функций от двух переменных осуществляется с помощью встроенной в ядро функции plot3d. Для построения графика функции в явном виде z = z(x,y) используется процедура plot3d(z,x = a..b, y = c..d,p), а для функции с параметрической формой задания x = x(t), y = y(t), z = z(t) – plot3d([x,y,z], a..b,c..d,p). Построение графиков функций заданных в явном виде:
> restart; > z[1]:=(x,y)->cos(x^2+2)*sin(y^2+2);
Ø plot3d(z[1](x,y),x=-10..10, y=-10..10,color=blue,thickness=1,axes=frame);
> restart; > z[2]:=(x,y)->cos(x*y)*sin(x*y);
> plot3d(z[2](x,y),x=-2..2, y=-2..2,color=blue,thickness=1,axes=boxed);
> restart;
> plot3d(sin(x^2+y^2)*x^2,x=-2..2, y=-2..2,color=blue,thickness=1,axes=normal);
> restart; > plot3d(sin(x^2+y^2)*x^2,x=-2..2,y=-2..2,style=hidden,color=blue,thickness=2); >
Построение графика функции в цилиндрической системе координат: > restart: > plot3d(h^2,a=-Pi..Pi, h=-5..5,coords=cylindrical,style=patch, title=" НЕЛИНЕЙНЫЙ КОНУС",thickness=1);
Трехмерные графики параметрически заданных поверхностей: > restart: > z[1]:=(t,u)->cos(t)*(1+0.2*sin(u));
> z[2]:=(t,u)->sin(t)*(1+0.2*sin(u));
> z[3]:=(t,u)->0.2*sin(t)*cos(u);
> plot3d([z[1](t,u),z[2](t,u),z[3](t,u)], t=-0.8..1.5*Pi, u=-Pi..0.7*Pi,thickness=1,axes=boxed);
> restart: > plot3d([(5+cos(t/2)*u)*cos(t),(5+cos(t/2)*u)*sin(t), sin(t/2)*u],t=0..2*Pi, u=-1..1,grid=[30,15],orientation= =[-130,30],titlefont=[HELVETICA,BOLD,20], title="Лист Мебиуса",shading=ZGREYSCALE);
В данном разделе приведены наиболее часто применяемые операторы для построения двумерных и трехмерных графиков функций, используемые для визуализации результатов исследований.
1.3. Вычисление пределов Для вычисления пределов функции f(x) при x->a используется следующая функция: limit(f(x),x = a, g), где f(x) — алгебраическое выражение, x — имя переменной, g — параметр, указывающий на направление поиска предела (left — слева, right — справа, real — в области вещественных чисел, complex — в области комплексных чисел. Значением a — может быть бесконечность (infinity), как положительная, так и отрицательная. Примеры применения этой функции приведены ниже:
> restart; > with(linalg): Warning, the protected names norm and trace have been redefined and unprotected
> Limit(f(x),x=a);
> Limit(sin(x)^tan(x),x=0)=limit(sin(x)^tan(x),x=0);
> Limit((1+(3/x)^x),x=infinity)=limit((1+(3/x)^x), x=infinity);
> Limit(arcsin(sqrt(x^2+x)+x),x=infinity)= =limit(arcsin(sqrt(x^2+x)+x),x=infinity);
> Limit((1/x)-(1/exp(x)-1),x=0)= =limit((1/x)-(1/exp(x)-1),x=0);
> Limit(((x+2^x)^(1/x)),x=infinity)= =limit(((x+2^x)^(1/x)),x=infinity);
> Limit(1-exp(-x),x=infinity)= =limit(1-exp(-x),x=infinity);
> Limit(exp(x),x=infinity)=limit(exp(x),x=infinity);
> Limit((Pi-2*x)*tan(x),x=Pi/2)= =limit((Pi-2*x)*tan(x),x=Pi/2);
> Limit(tan(x),x=Pi/2)=limit(tan(x),x=Pi/2);
> Limit(tan(x),x=Pi/2,right)=limit(tan(x),x=Pi/2,right);
> Limit(tan(x),x=Pi/2,left)=limit(tan(x),x=Pi/2,left);
Ø plot(tan(x),x=-5..5, y=-10..10,color=black,thickness=3);
1.4. Вычисление производных Вычисление производных функций — одна из самых распространенных задач математического анализа. Для ее реализации существует следующая функция: diff(a,x1,x2,..., xn) , где a — дифференцируемоле алгебраическое выражение или функция, x1, x2,..., xn — ряд переменных, по которым производится дифференцирование. Ниже приведены примеры применения функции diff. Вычисление производных явно заданных функций: > restart: > with(linalg): with(plots): 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|